Operaciones geométricas con datos vectoriales
Introducción
El análisis de los datos ráster se basa fundamentalmente en el análisis de sus valores. Esto es debido a que las entidades geográficas asociadas a esos valores (las celdas) presentan una regularidad estructural propia del formato, de la cual no se puede derivar nueva información. Más aún, según vimos en el capítulo Algebra_de_mapas , resulta necesario homogeneizar dicha estructura, lo cual centra la atención del análisis en los valores recogidos y no en las formas geométricas a las que dichos valores caracterizan.
Con los datos vectoriales, la situación es diferente. En el caso de datos vectoriales, las entidades asociadas a cada atributo tienen sus propias características espaciales y la geometría que definen sirve por sí sola para llevar a cabo numerosos análisis. Si la unimos a los atributos que esta geometría lleva asociados, tenemos la posibilidad de realizar un número mayor de dichos análisis.
En este capítulo veremos una serie de operaciones que transforman los datos vectoriales actuando sobre sus geometrías, con el concurso en algunos casos de los atributos de estas. Los resultados de estas operaciones son nuevas capas cuyas geometrías aportan información adicional a las geometrías originales, o bien las transforman para que su uso sea más adecuado en otros análisis u operaciones.
Una buena parte de estas operaciones trabajan con dos capas, siendo similares en concepto (que no en la naturaleza de las operaciones que implican) a las funciones de tipo local del álgebra de mapas, empleadas para combinar varias capas con distintos valores. Otras requieren una sola capa, y aplican transformaciones en función de valores y geometrías o simplemente geometrías, pudiendo considerarse en cierta forma el equivalente a las funciones focales del álgebra de mapas ráster.
Muchas de las operaciones geométricas que pueden realizarse con datos vectoriales pueden llevarse a cabo empleando el álgebra de mapas de capas ráster si disponemos de la misma información en ese formato. Otras, sin embargo, no son adecuadas para efectuarse sobre una base ráster, del mismo modo que algunas operaciones del álgebra de mapas no se pueden llevar a cabo (o al menos no de una forma que resulte adecuada) utilizando datos vectoriales.
Esta equiparación entre el álgebra de mapas ráster y estas transformaciones geométricas (también una especie de álgebra de mapas vectorial, en cierta medida) puede plantear una disyuntiva desde el punto de vista del usuario de SIG que pretende analizar sus datos. Utilizar uno u otro modelo a la hora del análisis representa una elección igual que lo es el optar por una u otra forma de almacenamiento, vayamos o no a efectuar análisis sobre los datos almacenados. Sin embargo, no son opciones mutuamente excluyentes, y lo ideal es conocer los puntos fuertes y débiles de cada planteamiento, para así combinar ambos de la mejor forma posible. Como ya sabemos, los SIG hoy en día no son puramente ráster o vectoriales, sino que incluyen herramientas con ambos planteamientos. Utilizarlas conjuntamente es la forma más idónea de aprovechar toda su potencia.
Zonas de influencia
Una de las transformaciones más importantes con capas vectoriales es la creación de zonas de influencia, también conocidas como buffers }. Esta transformación puede llevarse a cabo con entidades de tipo punto, línea o polígono, y su resultado siempre es una nueva capa de polígonos. Las áreas cubiertas por estos polígonos reflejan las zonas de influencia de cada entidad, influencia que se considera la ejerce hasta una distancia dada. Pueden verse también de forma inversa, como una influencia recibida, de tal modo que todos los elementos dentro de la zona de influencia afectan a la entidad que la genera.
Por ejemplo, comenzando con un ejemplo de entidades puntuales, sea un conjunto de antenas de radio y una coordenada que representa la posición en la que nos encontramos. Si estas antenas tienen un alcance máximo (una dimensión máxima de su zona de influencia), es sencillo ver si estamos dentro de dicho alcance y recibimos la señal de alguna o varias de ellas. Para ello, basta crear zonas de influencia de los puntos donde se sitúan las antenas y después comprobar si el punto donde nos situamos esta dentro de alguna de dichas zonas. Para esto último, ya conocemos formulaciones específicas como las que vimos en Calculos_espaciales_basicos .
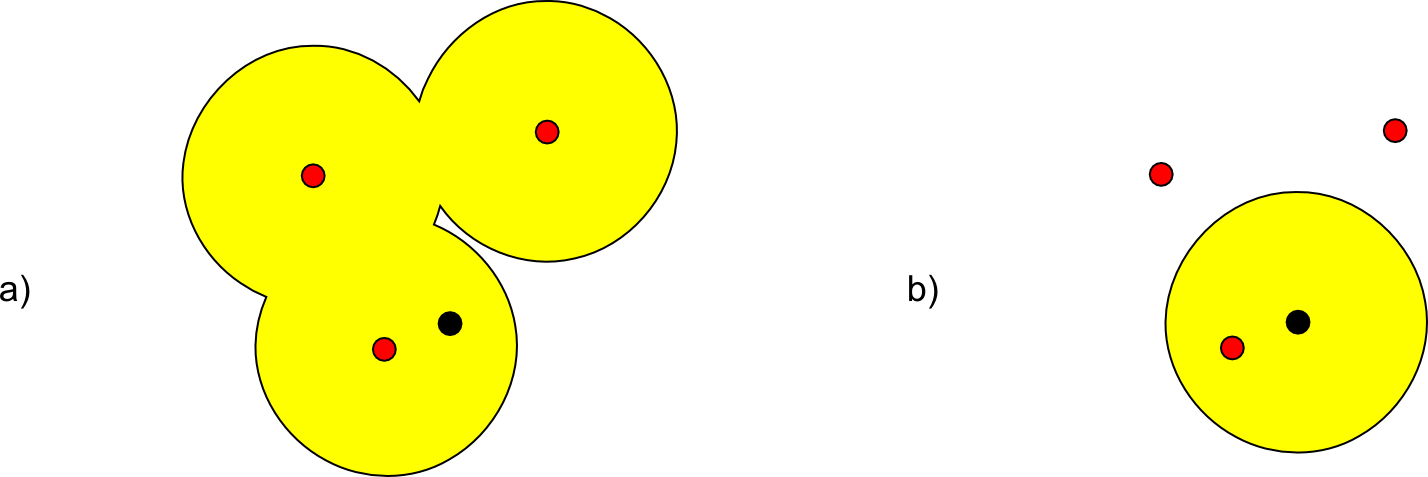
Como se muestra en la figura \ref{Fig:Zona_influencia_circular}, este análisis se puede realizar de dos formas distintas, según se considere la influencia ejercida por las distintas antenas o la recibida por el punto de análisis. En el caso a), se calculan las zonas de influencia correspondiente a cada una de las antenas, y posteriormente se comprueba si el punto analizado se encuentra en el interior de alguna de ellas. En el caso b), por el contrario, el planteamiento es opuesto. Tomando el punto donde nos encontramos, calculamos una zona de influencia alrededor de dicho punto, y después comprobamos si alguna de las antenas cae dentro de esta zona. En ambos casos, si esa comprobación tiene un resultado positivo nos encontramos en un punto de cobertura. Si el resultado es negativo, estamos fuera del alcance de las antenas.
El hecho de poder plantear este análisis de dos formas distintas es debido a que, según lo visto en Calculos_espaciales_basicos , en un espacio métrico se tiene que, para dos puntos A y B, la distancia entre A y B ($d_{AB}$) es igual a la distancia entre B y A ($d_{BA}$). Pueden calcularse zonas de influencia basadas en otro tipo de medidas que no cumplen la anterior propiedad, aunque las operaciones correspondientes se llevan a cabo sobre capas en formato ráster, y las estudiaremos en el capítulo Costes .
Calcular una zona de influencia de un punto es un procedimiento sumamente sencillo, ya que esta zona es simplemente un circulo centrado en el punto y con radio la distancia máxima de influencia. En el caso de considerar líneas en lugar de puntos, la operación es conceptualmente similar, aunque el algoritmo subyacente es notablemente más complejo. No obstante, la interpretación es idéntica.
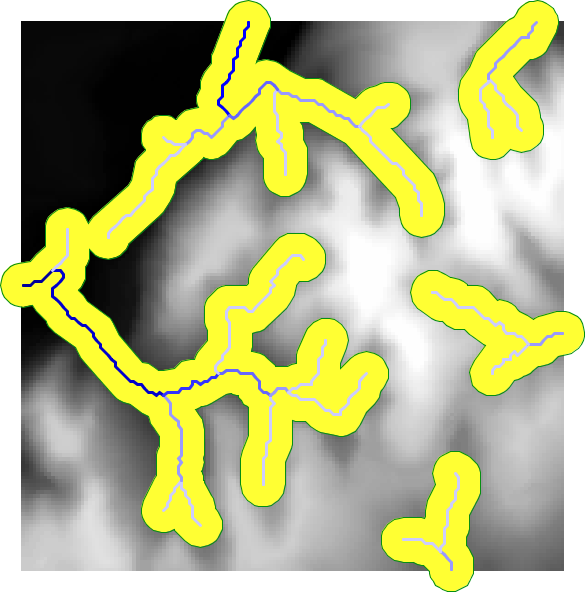
En la figura \ref{Fig:Zona_influencia_lineas} podemos ver cómo el trazado de un cauce se transforma en un área que engloba todos aquellos puntos que se sitúan a una distancia del cauce menor que el umbral establecido.
Podemos utilizar este tipo de zonas de influencia para, por ejemplo, estudiar qué industrias pueden afectar la calidad de las aguas de un río. Teniendo el trazado de este río y el emplazamiento de las industrias, podemos hacer una zona de influencia del cauce para una distancia máxima de influencia y ver cuáles de estas últimas se sitúan dentro de ella.
De igual modo que en el ejemplo anterior, el análisis se pueden plantear de forma contraria, calculando las zonas de influencia de cada industria y viendo si estas cortan al trazado del cauce. Aquí podemos ver que, aunque los procedimientos para puntos y líneas sean distintos, su significado es el mismo, y por ello pueden utilizarse las zonas de influencia creadas a partir tanto de unas como de otras geometrías, indistintamente.

En el caso de polígonos, y puesto que ya conforman regiones, las zonas de influencia pueden establecerse no solo hacia el exterior, sino también hacia el interior de la geometría (Figura \ref{Fig:Zona_influencia_poligonos}). En el caso de extender el área del polígono, la interpretación es la misma que en los ejemplos anteriores. Por ejemplo, para un polígono que delimita el perímetro de un núcleo urbano, su zona de influencia puede indicar la extensión de territorio al que los habitantes de ese núcleo podrían desplazarse en busca de algún servicio, o bien la de la región de procedencia de quienes pueden acudir a la ciudad en busca del mismo. Una zona de influencia hacia el interior, sin embargo, nos indicaría, por ejemplo, qué habitantes no es probable que salgan del núcleo urbano en busca de un servicio dado, ya que este desplazamiento es demasiado costoso.
Otro uso habitual de este tipo de zonas de influencia la encontramos en la gestión de costas. Si consideramos una zona de protección costera de una distancia dada, el polígono de influencia calculado hacia el interior con esa distancia representa las zonas a más de dicha distancia de la costa. Por tanto, representa a aquellas zonas fuera de la zona de protección, que serán aquellas sobre las que puedan establecerse actividades tales como la edificación o la implantación de infraestructuras.
Mientras que la zona de influencia exterior no tiene ningún límite, la trazada hacia el interior viene limitada por las propias dimensiones del polígono de origen.
Sobre la base anterior de zonas de influencia delimitadas a partir de las geometrías fundamentales, existen muchas variantes y formas de construirlas. Un proceso habitual es la creación no de una única zona de influencia para cada entidad base, sino de un conjunto de ellas equiespaciadas, de tal forma que puedan considerarse distintos grados de influencia. Este conjunto de zonas de tamaños sucesivos forman una serie de polígonos concéntricos que pueden, además, representarse de forma distinta para reflejar más explícitamente su significado.
Es fácil ver que si se trazan dos áreas de influencia de tamaño $r$ y $2r$ a partir de una geometría de un tipo cualquiera, esta última es equivalente al área de influencia creada a partir de la primera, con distancia $r$.
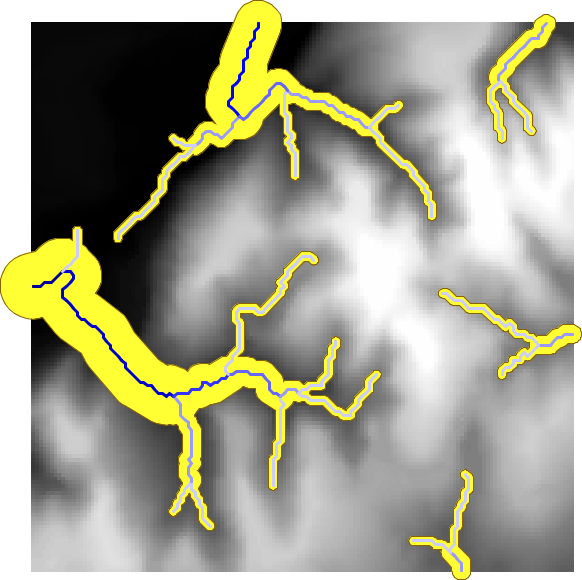
La dimensión de una zona de influencia no debe ser constante para todos los elementos que componen la capa de base. Considerando el caso de una capa de cauces, no parece lógico considerar que todos los cauces van a tener una zona de influencia idéntica. Los cauces con un mayor caudal deberían tener una zona de influencia mayor, mientras que los pequeños afluentes deberían estar asociados a zonas de influencia menores.
Trabajando con una capa de puntos en lugar de una de líneas, como la mencionada en el ejemplo de las antenas, pudiera darse una situación en la que no todas ellas tuvieran la misma potencia y el alcance de su señal fuera distinto en cada caso. En este supuesto debería establecerse un radio distinto para los círculos de influencia de cada antena.
Tanto el caudal del cauce como la potencia de la antena son atributos de la entidad que estarán en su correspondiente tabla de atributos. Utilizando estos, pueden crearse capas de influencia variables que tengan en cuenta las características puntuales de cada elemento geográfico. Es decir, se toma en cada caso la dimensión del área de influencia de la tabla de atributos, en lugar de ser un valor fijo.
La figura \ref{Fig:Zona_influencia_variable} muestra el aspecto de una zona de influencia calculada a partir de una red de drenaje, cuya dimensión se establece en función del orden jerárquico de cada tramo.
Otra de las modificaciones que se pueden plantear a la creación de zonas de influencia es la simplificación de estas cuando existen solapes. En el resultado del caso a) la figura \ref{Fig:Zona_influencia_circular} puede verse cómo las distintas zonas de influencia se solapan en algunos puntos. No obstante la zona global que se ve afectada por la presencia de los puntos (antenas según suponíamos para el ejemplo), puede recogerse de igual modo con un único polígono, ya que, puesto que existe contacto entre las zonas, puede simplemente considerarse el contorno del conjunto.
En general, todas las entidades geográficas se prestan a la creación de zonas de influencia sin ninguna consideración especial. No obstante, en el caso de curvas o polígonos muy convolucionados, pueden en ocasiones darse formas incoherentes.
Operaciones de solape
Las operaciones de solape son equivalentes a las expresadas en el álgebra de mapas mediante funciones locales con varias capas ráster. Estas operaciones permiten generar nuevas capas vectoriales a partir del cruce de dos de ellas, pudiendo dichas capas de origen contener distintos tipos de entidades, aunque principalmente regiones (polígonos).
La naturaleza de estas operaciones es bien distinta a la de sus equivalentes ráster. Por una parte, se basan en cálculos geométricos que utilizan las coordenadas de cada entidad para obtener nuevas entidades resultantes. Por otra, se aplican operaciones lógicas sobre las capas de entrada para generar los resultados. Estas operaciones de tipo lógico (verdadero/falso), que como vimos también pueden aplicarse celda a celda entre dos capas ráster, son las que definen cada una de las operaciones de solape.
En dichas operaciones se aplican los conceptos de relaciones espaciales vistos en Relaciones_espaciales , y es en función de ellos como, a partir de los resultados geométricos, se generan las nuevas capas.
Encontramos los siguientes tipos de operaciones de solape:
- Recorte
- Diferencia
- Intersección
- Unión
Recorte
Una de las aplicaciones que veíamos de las funciones locales para capas ráster era la combinación con objeto de restringir la extensión de una capa de entrada. Utilizábamos una capa con la información de interés y otra con una «máscara», la cual indicaba qué celdas resultaba de interés preservar en la capa resultante.
En el caso vectorial, la operación de recorte toma una capa con cualquier tipo de entidades donde se contienen la información a recortar, y otra capa de polígonos que contiene aquellas regiones que resultan de interés. La capa resultante mantiene el mismo tipo de información, pero solo mantiene aquellas entidades que se incluyen total o parcialmente dentro de alguno de los polígonos de recorte, modificando dichas entidades cuando corresponda.
Esta operación se conoce como clipping en inglés y es habitual verla así citada o implementada en los SIG.
En la figura \ref{Fig:Recorte_vectorial} podemos ver cómo la capa de entrada con polígonos, líneas y puntos se restringe a una extensión menor manteniendo dentro de dicha zona la misma información original. Se considera en este ejemplo un único polígono de recorte, pero pueden ser varios, e incluso polígonos con huecos interiores, sin que exista diferencia alguna en la operación.
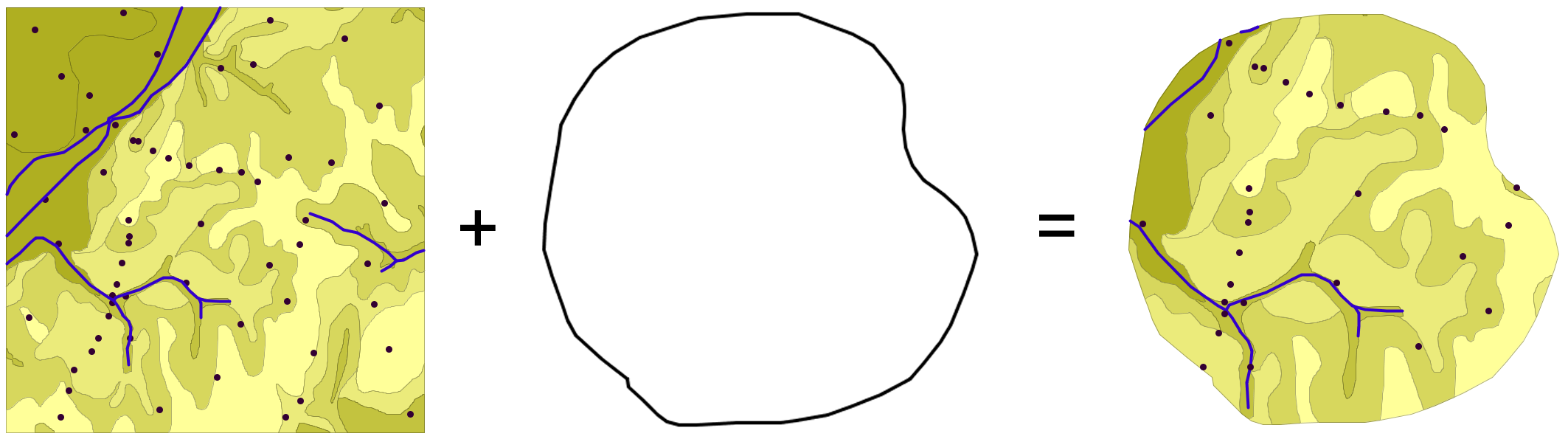
Para los puntos, solo se mantienen aquellos que se sitúan dentro del polígono de recorte. Para las líneas, se mantienen aquellas que entran dentro del polígono o lo cruzan, recortándose para que no salgan de este. Y en el caso de polígonos, estos se recortan para restringir su extensión a la del polígono de recorte.
Un aspecto muy importante en el recorte de capas vectoriales es el tratamiento de las tablas de atributos asociadas a cada elemento. Salvo en el caso de puntos, en el caso de recortar alguna capa de otro tipo, las geometrías de esta se modifican, y la capa resultante contiene la geometría modificada y el mismo registro original asociado a ella.
Cuando la capa recortada es de puntos, no existe problema en esto, ya que no se da modificación alguna de las geometrías. El recorte es en realidad una operación de consulta y selección. La información de la tabla sigue correspondiéndose con la entidad geométrica, ya que ninguna de las dos ha cambiado. Cuando se recortan líneas o polígonos, sin embargo, la situación es algo más compleja.
Supongamos que la capa recortada es de polígonos tales como unidades administrativas. Si el registro original contiene información tal como por ejemplo el nombre de la unidad o su código postal asociado, no existe ningún problema, ya que estos valores se aplican de igual modo para la parte de cada polígono que quede tras el recorte. Una situación muy distinta la tenemos, sin embargo, cuando la tabla de atributos contiene valores tales como el área, el perímetro o el número de habitantes de dicha unidad administrativa. En este último caso, dichos valores guardan una relación directa con la geometría, y al cambiar esta deberían modificarse igualmente.
La operación de recorte no actúa sobre las tablas de atributos, ya que no posee información suficiente para poder hacerlo. Tanto el área como el perímetro deben recalcularse para que la información de la tabla de atributos sea coherente con el nuevo polígono al que se encuentra asociada. Como ya sabemos, medir estas propiedades de un polígono es sencillo a partir de sus coordenadas, y debe simplemente tenerse esa precaución. Se tiene que el recorte de la capa no es únicamente una operación geométrica, sino que, según sean los valores de la tabla de atributos, debe operarse también con ellos para completar dicha operación.
El caso del número de habitantes es algo distinto al del perímetro o el área, ya que no es una propiedad puramente geométrica. Puede calcularse el número de habitantes del polígono recortado aplicando una mera proporción entre las superficies original y recortada, pero el valor resultante solo será correcto si la variable (es decir, el número de habitantes) es constante en el espacio. Entramos aquí en el problema de la falacia ecológica, el cual vimos en la sección MAUP , y que es de gran importancia a la hora de aplicar operaciones de solape.
Cuando la capa recortada es de líneas, debe considerarse de igual modo el hecho de que ciertas propiedades dependen directamente de la geometría, y por tanto definen la línea completa, no la parte de esta que queda tras el recorte. La longitud es un claro ejemplo de esto. Al no constituir regiones, el Problema de la Unidad de Área Modificable y otros problemas derivados no se han de considerar de la misma forma que en el caso de capas de polígonos, pero es necesario igualmente estudiar los valores de la tabla de atributos, para ver cómo el recorte de la capa afecta al significado de estos.
Diferencia
La diferencia es un operador contrario al recorte. En este último, como hemos visto, se mantienen en la capa resultante las geometrías de la capa recortada que entran dentro del área de recorte definida por otra capa adicional. En la diferencia, el proceso es semejante, pero en este caso las zonas que se mantienen son las que no entran dentro de la zona definida por la capa de recorte.
Puede entenderse como la realización de un recorte, pero en lugar de utilizando un conjunto de polígonos de recorte, empleando su complementario.
Mientras que el recorte era útil para restringir la información de una capa vectorial a un área dada, la diferencia es útil cuando deseamos excluir dicho área de la capa. Por ejemplo, dada una zona de influencia de un cauce, recogida esta en una capa vectorial de polígonos, puede interpretarse de cara a una planificación del terreno como una zona no apta para la edificación. A la hora de llevar a cabo un estudio relativo a dicha edificación, es interesante eliminar las zonas de influencia, ya que no van a tenerse en cuenta de ahí en adelante al no ser aptas para la actividad analizada.
Por su similar naturaleza, todas las consideraciones anteriormente hechas para el caso del recorte deben igualmente tenerse presentes al aplicar la operación diferencia.
Intersección
La intersección es equivalente a una operación booleana Y (AND), ya que la capa resultante mantiene solo aquellas zonas para las que se dispone de información en ambas capas de entrada. Es decir, aquellas zonas donde hay entidades en ambas capas. En particular, estas entidades han de ser de tipo polígono.
A diferencia del recorte, la información empleada para crear la tabla resultante no proviene únicamente de una capa (la capa recortada), sino de ambas capas de origen. Por ello, se producen modificaciones en las geometrías, que se dividen (se «trocean») según sea la intersección con las geometrías de la otra capa, y también en las tablas de atributos. Los atributos de cada una de las nuevas entidades son todos los asociados a las entidades que han dado lugar a dicha entidad intersección. Puesto que solo se mantienen en la capa resultante las entidades donde exista coincidencia, siempre habrá información en ellas sobre ambas capas. Es decir, la tabla de atributos resultante tiene tantos campos como el conjunto de las dos capas de partida.
Puede verse un sencillo ejemplo en la figura \ref{Fig:Interseccion_vectorial}.
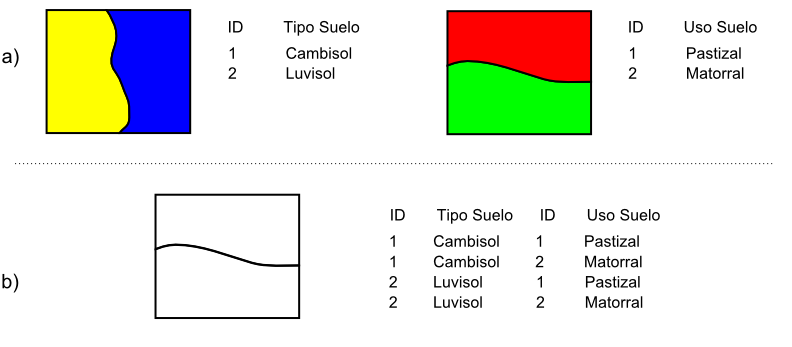
El hecho de que en la tabla aparezcan dos campos con el mismo nombre no implica que deban en modo alguno «mezclarse» los valores de estos. Simplemente existirán en la tabla resultante dos campos distintos con un nombre coincidente.
Al igual que en el caso anterior, de existir capas con valores que guarden relación con el área de cada polígono, los valores en las tablas pierden su significado al llevar a cabo la intersección. De hecho, podrían existir en ambas capas de origen sendos campos con un valor de área, que aparecerían ambos en la tabla de la capa resultante. Ninguno de ellos, no obstante, sería aplicable a la entidad a la que hacen referencia.
Este caso que acabamos de ver es idéntico en concepto al que veíamos en el apartado Funciones_locales sobre combinación de capas mediante el álgebra de mapas. Si se recuerda lo visto entonces, era necesario codificar de forma particular los valores en las capas de entrada para llevar a cabo correctamente la operación de combinación. Esto era así porque la capa resultante debía contener la información de las dos capas de entrada (tipo de suelo y uso de suelo, en aquel ejemplo), pero debía almacenar dicha información en un único valor, ya que una capa ráster tiene tan solo un valor asociado a cada celda.
Al trabajar con capas vectoriales, no existe esa limitación, y cada entidad puede llevar asociados tantos campos como se quiera. Por esta razón, no es necesario «preparar» las capas de entrada y modificar sus valores, ya que toda la información que contienen puede incorporarse a la capa resultante sin más que añadir los campos en los que se encuentra.
Unión
Si la intersección se puede asimilar a un operador lógico Y (AND), la unión es semejante al operador lógico O (OR). En la capa resultante del proceso aparecen todas las geometrías de la intersección y, junto a estas, también aquellas que corresponden a las zonas que aparecen únicamente en una de las capas de origen. Al cruzar estas capas, y al igual que en el caso de la intersección, sus geometrías se «trocean», pero en este caso todos esos «trozos» obtenidos aparecen en la capa resultante, y no solamente algunos de ellos.
De esta forma, y al unir dos capas de polígonos, encontraremos en la capa resultante zonas que están cubiertas por uno de ellos perteneciente a la primera capa, o bien por uno de la segunda capa, o bien por polígonos de ambas capas. Si, por ejemplo, esas capas representan zonas de influencia de dos procesos, podremos de este modo conocer cuáles afectan a cada una de las geometrías resultantes, y saber si, dentro del perímetro de dicha geometría, estamos dentro de la zona de influencia de ambos procesos, o bien solo en la de uno de ellos.
En general, la unión resulta de interés cuando estudiemos la existencia de dos fenómenos y queramos ver dónde tiene lugar al menos uno de dichos ellos. En la intersección buscábamos conocer en qué lugares tenían lugar los dos fenómenos simultáneamente.
La tabla de atributos correspondiente es igual a la de la intersección, con tantos campos como el conjunto de las dos capas de partida. En esta ocasión, no obstante, y por existir polígonos resultantes que no aparecerían en la intersección (zonas donde solo uno de los fenómenos representados se produce), aparecerán campos sin información, ya que no existen información suficiente para asignarse en esos casos.
La figura \ref{Fig:Union_vectorial} muestra un ejemplo de unión de capas vectoriales.
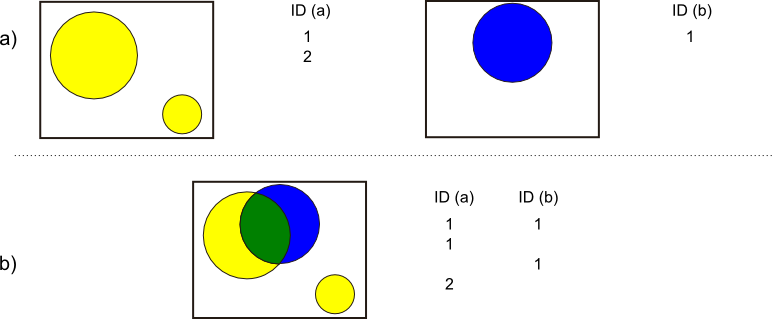
Polígonos espúreos
Las operaciones geométricas de solape cruzan las geometrías de dos capas y calculan los elementos resultantes de la combinación de estas. Al llevar esto a cabo, es probable que en ciertos lugares existan líneas de estas capas que debieran coincidir pero que, debido a imprecisiones en su digitalización o a la precisión particular de cada capa, no lo hagan exactamente. Es decir, una misma realidad queda registrada de formas distintas en las diferentes capas de origen.
A la hora de efectuar la combinación anterior, esa falta de coincidencia va a dar lugar a polígonos adicionales que no deberían estar ahí. Estos, además, serán de pequeño tamaño, ya que las imprecisiones son pequeñas en relación al tamaño de las geometrías intersecadas. Estos polígonos son artificios fruto de las imprecisiones existentes en las capas sobre las que se realiza la operación geométrica en cuestión, y su eliminación es un paso complementario a dicha operación, el cual debe llevarse a cabo igualmente.
La aparición de polígonos espúreos (también frecuentemente citados en su denominación inglesa, sliver polygons ) puede evitarse a la hora de realizar la intersección, incorporando en los algoritmos correspondientes una cierta tolerancia que permita que líneas distintas puedan tratarse como idénticas(como deberían ser en realidad), siempre que la diferencia entre ellas no supere dicha tolerancia.}
Otra solución es la eliminación a posteriori , tratando de localizar los polígonos espúreos diferenciándolos de aquellos que sí representen regiones reales que deben conservarse. Algunas de las características que suelen presentar habitualmente y que pueden emplearse para esa distinción son:
- Pequeño tamaño
- Forma alargada
- Bajo número de lados. Son polígonos simples con pocos segmentos.
La figura \ref{Fig:Poligonos_espureos} muestra un ejemplo de la aparición de este tipo de polígonos.
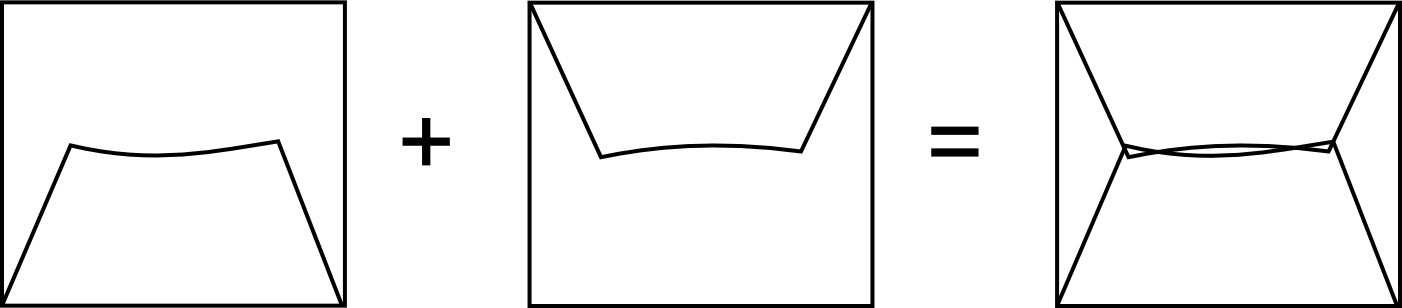
Juntar capas
Juntar capas no es una operación geométrica propiamente dicha, ya que ninguna de las geometrías de las capas de entrada se ve alterada en lo que a sus coordenadas respecta. Es, no obstante, una operación de combinación, ya que, al igual que las anteriores, genera una nueva capa de datos espaciales vectoriales a partir de dos capas de partida. En realidad puede aplicarse sobre un número $n$ de capas, aunque por simplicidad suponemos que estas son solo dos.
El resultado es una nueva capa que contiene la información de las dos capas de entrada, es decir todas las entidades que se encuentran en una u otra de estas. Sobre dichas entidades no se realiza ningún análisis geométrico, y el hecho de que estas intersequen o no carece de relevancia para el resultado. Las relaciones espaciales entre entidades de ambas capas no se tienen en cuenta.
Por ello, si dos entidades por ejemplo poligonales, una de cada una de las capas de partida, se intersecan, ambas aparecerán en la capa resultante como tales, sin verse afectadas. En la zona de intersección habrá dos polígonos distintos. Esto no sucedía en las operaciones de solape vistas anteriormente.
La parte principal de la operación no es, por tanto, la relativa a las geometrías, ya que estas simplemente se «reúnen» en una sola capa. La consideración más importante es la que respecta a la información asociada a la capa resultante, que proviene de las dos capas de origen y define realmente el significado de esta.
La tabla de la capa resultante contiene tantos elementos como existan en el conjunto de capas de partida. Si estas contienen respectivamente $n$ y $m$ elementos, la capa resultante tendrá $n + m$ entidades. Para cada elemento se recogen tantos campos como campos diferentes aparezcan entre las dos tablas. Las entidades de una de las capas, si no tienen valores para los campos provenientes de la otra —por no aparecer este campo en ambas— no tendrán valor alguno. Algunos SIG dan la opción de seleccionar qué capa es la capa principal, cuyos campos se emplearan para la capa definitiva. La información de las otras capas que se recoja en campos no existentes en dicha capa principal se perderá en la capa resultante. Con independencia de la implementación, el concepto es similar en todos los casos.
Para comprender mejor esta operación, puede verse un ejemplo en la figura \ref{Fig:Ejemplo_juntar_capas}.

Para aplicar esta operación de forma coherente y que la tabla generada según lo anterior tenga pleno sentido, ambas capas de origen tienen que contener no solo el mismo tipo de entidades, sino también información de índole similar. Salvo en contadas ocasiones, no tiene sentido unir, por ejemplo, una capa de polígonos y otra de líneas, y será mejor mantenerlas independientes a todos los efectos. De modo similar, tampoco tiene sentido unir una capa de polígonos con valores de uso de suelo y otra con límites administrativos, ya que las tablas de datos de estas serán bien distintas y el resultado será poco coherente. La similitud en cuanto al tipo de entidad no garantiza que la operación tenga sentido.
La operación de juntar capas es útil en muchas circunstancias en las cuales se dispone de datos geográficos de distintas procedencias o que, por su propio origen, vienen divididos en partes. Un caso frecuente es el de disponer de la información por hojas coincidentes con la cartografía clásica, tales como las hojas proporcionadas por los Institutos Geográficos o instituciones similares. Si la zona estudiada cubre varias de estas hojas, tendremos los datos divididos en tantas capas distintas como hojas cubiertas. Sin embargo, lo ideal sería tenerlas todas en una única capa.
Esta conveniencia no solo es relativa al manejo de la capa, sino también para otros aspectos tales como el análisis o incluso la visualización. A la hora de analizar los datos, muchas formulaciones utilizan no solo la geometría o los valores asociados a esta, sino también la relación con otros elementos de la misma capa. Tal es el caso en el análisis de redes, por ejemplo. Si la red de carreteras que recorre esas hojas en las que se sitúa la zona de estudia se encuentra en diversas capas, no se refleja la conectividad entre las carreteras de distintas hojas. Deben juntarse en una única antes de poder analizarlas conjuntamente.
Otras operaciones no requieren de esa conectividad, pero el aplicarlas sobre la información contenida en las capas implica hacerlo tantas veces como capas existan. En lugar de calcular, por ejemplo, un área de influencia de dichas capas, hay que calcular ese mismo área para cada capa. Después estas zonas de influencia podrían juntarse en una sola capa, pero resulta más lógico hacerlo a priori y después operar.
Juntando las capas, la visualización también se ve afectada. Además de no poder analizar conjuntamente ese conjunto de carreteras cuando están en capas separadas, tampoco pueden modificarse conjuntamente los atributos de representación. Cambiar el color o el grosor de las líneas que representan las carreteras implica cambiar ese color o grosor para cada una de las capas, para que el resultado sea visualmente homogéneo.
Si la paleta de colores no es de tipo absoluta y no utiliza una tabla de asignación, sino que adapta una rampa de colores entre los valores mínimos y máximos del campo utilizado para asignar los colores, es absolutamente necesario unir las capas que queramos para conseguir un resultado coherente. De otro modo, la misma rampa de colores no representará lo mismo en cada capa, ya que los máximos y mínimos entre los que se adapta serán distintos para cada parte (cada capa), y en el caso más habitual distintos asimismo de los correspondientes al total de los datos de la zona de estudio. Veremos un ejemplo de esto en el capítulo SIGs_escritorio .
Pueden juntarse capas no solo porque abarquen áreas distintas con una misma información, sino también si cubren el mismo área pero con informaciones distintas. Estas informaciones deben compartir, no obstante, algún rasgo común. Una capa de carreteras y otra con caminos pueden juntarse para formar una capa con las vías existentes en la zona de estudio.
Modificaciones basadas en atributos. Disolución
Las tablas de atributos pueden emplearse para definir la forma en que se realiza una operación geométrica. En lugar de ser elementos pasivos que no se ven modificados tras la operación, los atributos pueden ser quienes aporten la información necesaria para establecer la manera de modificar las entidades de entrada.
Una operación muy frecuente en este sentido es la llamada disolución . Esta operación recibe este nombre debido a que une polígonos con atributos comunes y «disuelve» las fronteras existentes entre ellos en una única entidad. No es necesario que exista una frontera entre los polígonos (es decir, que sean contiguos) ya que pueden almacenarse en una capa vectorial entidades compuestas por varios polígonos disjuntos. Tal es el caso, por ejemplo, de una entidad poligonal que represente a España, que contendrá no solo el polígono de la península, sino también los de las islas que pertenecen igualmente al país. Para todos ellos existe un único registro en la tabla de atributos asociada.
La aplicación de la operación disolver hace que todos aquellos polígonos que tengan asociado un determinado valor en uno de sus atributos pasen a constituir una nueva y única entidad, ya sea esta de un solo polígono o varios disjuntos.
Este es el caso que aplicábamos, por ejemplo, a la hora de simplificar las zonas de influencia. En dicho caso, se unen simplemente por contigüidad espacial todas las zonas generadas, asumiéndose por tanto que todas tienen algún valor común en sus atributos.
No obstante, pueden disolverse las entidades según distintos grupos, tantos como valores distintos de un atributo existan en la capa. Un ejemplo muy representativo en este sentido es obtener a partir de una capa con provincias una nueva con polígonos que representen comunidades autónomas. Es decir, agrupar un tipo de división en otra a una escala mayor. Para ello, por supuesto, debe existir información sobre a qué comunidad autónoma pertenece cada provincia, para poder aplicar la condición que permita seleccionar los polígonos a disolver.
En la figura \ref{Fig:Disolver} se muestra un ejemplo de lo anterior.
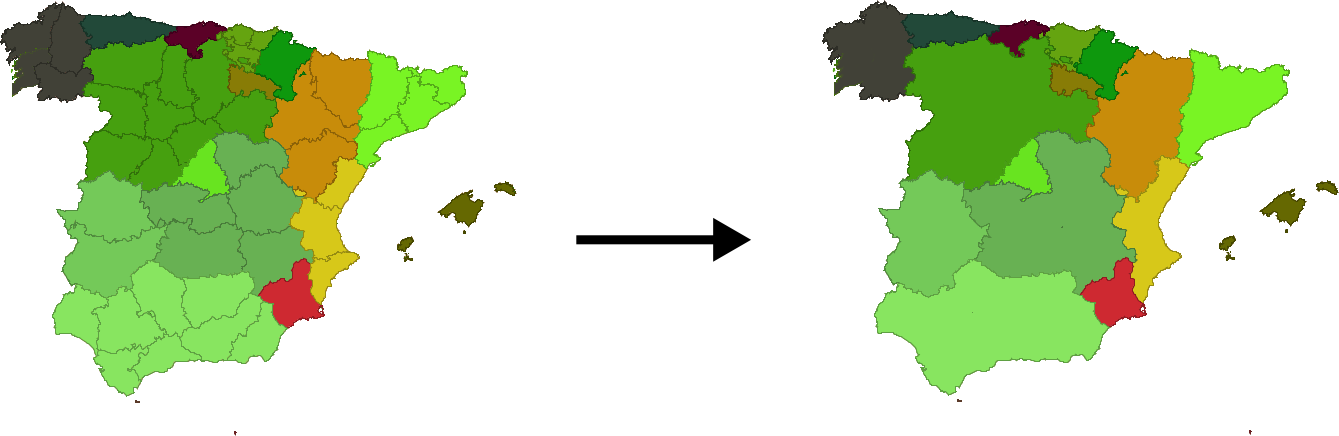
Al igual que en otras operaciones ya vistas, la tabla de atributos de la capa resultante merece atención aparte. En esta ocasión, existe un comportamiento diferente según si el atributo es numérico o no. Si el campo no es de tipo numérico, la unión de $n$ entidades en una única implica «juntar» la información $n$ valores no numéricos. Puesto que estos no permiten operaciones de tipo matemático, no es posible utilizar esos valores y obtener un valor para ese campo en la nueva capa. Por ello, estos campos no aparecerán en la tabla resultante.
En el caso de campos numéricos, pueden emplearse los datos de las capas de partida, aplicando operaciones diversas según sea la naturaleza de la variable. Por ejemplo, para un campo con el número de habitantes de cada término municipal, si aplicamos una operación de disolución y obtenemos una capa de comunidades autónomas, el valor de población de cada entidad resultante (cada comunidad autónoma), será la suma de los valores de los polígonos que han sido «disueltos» para obtener dicha entidad.
Si el campo en cuestión recoge la estatura media de la población, el valor resultante deberá ser una media ponderada de los valores de cada término, utilizando el número de habitantes como ponderación. Si en lugar de la media se recoge la estatura máxima, el máximo de todos los valores de los términos será el valor a incluir en la tabla de atributos de la capa resultante en ese campo.
Una vez más, es necesario considerar la naturaleza de la variable para establecer la forma de combinar los valores. Al hacerlo, y al igual que en otros casos, no deben perderse de vista los efectos derivados de la agregación que llevamos a cabo, los cuales ya conocemos.
Contornos mínimos
Dado un conjunto de puntos, una de las operaciones geométricas más comunes que pueden llevarse a cabo es la delimitación de un contorno mínimo que los englobe. Conocer el espacio ocupado por este contorno puede ser útil para evaluar diversos parámetros tales como la zona de cobertura del fenómeno representado por dichos puntos.
Existen diversas formas de contornos mínimos, entre las que cabe destacar.
- Envolvente convexa mínima
- Rectángulo mínimo
- Círculo mínimo
Envolvente convexa mínima (convex hull)
La envolvente convexa mínima (habitualmente citada como convex hull , su denominación en inglés) es la más común de las envolventes. Define el polígono convexo de menor área dentro del cual se contienen todos los puntos del conjunto, y su significado tanto geográfico como geométrico es de gran importancia.
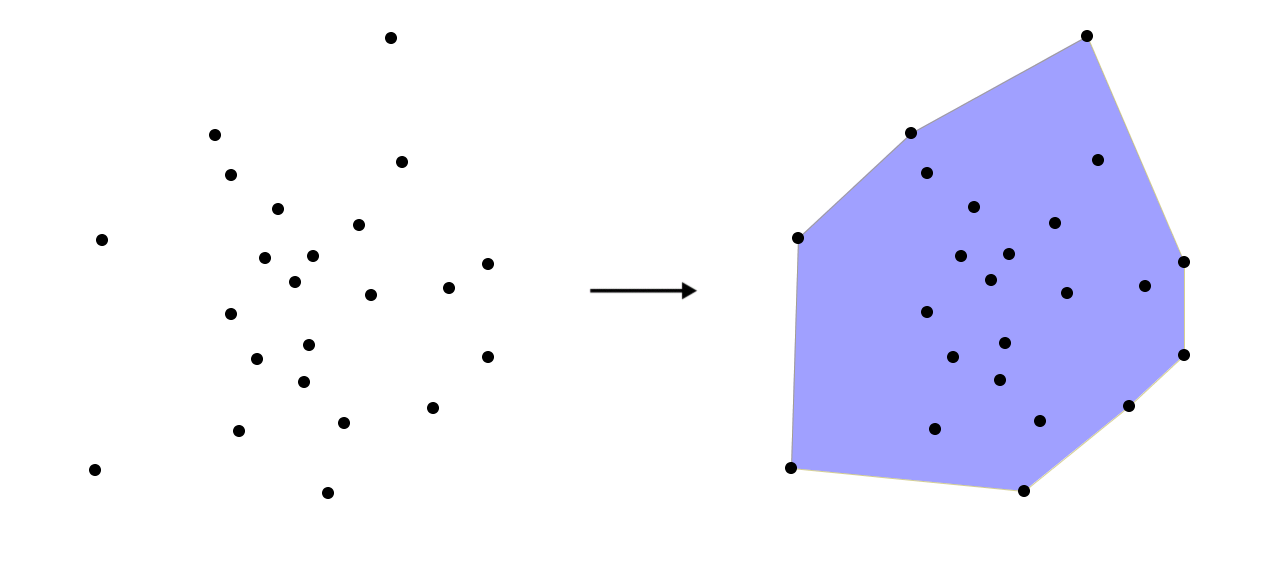
Resulta fácil visualizar el concepto de esta envolvente si suponemos que rodeamos los puntos con una banda elástica. La forma que define dicha banda es la envolvente mínima convexa. Como puede verse en la figura \ref{Fig:Convex_hull}, es sencillo trazar este polígono visualmente a partir de los puntos, pero su cálculo numérico es sumamente más complejo de implementar de lo que en apariencia puede pensarse. Los detalles acerca de algoritmos para el cálculo de esta envolvente pueden encontrarse, por ejemplo, en[ Rourke1998Cambridge ].
La envolvente convexa delimita el área dentro de la cual se puede inferir el comportamiento de una variable a partir de una serie de muestras. Por ejemplo, en el caso de interpolar un conjunto de valores tal y como vimos en el capítulo Creacion_capas_raster , los valores estimados dentro de la envolvente convexa mínima son producto de una interpolación, mientras que estimar valores fuera de dicha envolvente constituye en realidad un proceso de extrapolación.
El polígono que define a la envolvente mínima convexa puede ser empleado asimismo como dato de entrada para otras operaciones geométricas. Dados, por ejemplo, una serie de puntos en los que ha aparecido una enfermedad infecciosa,puede calcularse la envolvente mínima convexa y a partir de ella calcular una zona de influencia con una distancia definida en función de la capacidad de propagación de la enfermedad. El nuevo polígono resultante representa la región que puede verse afectada por dicha enfermedad.
Una serie de envolventes convexas sucesivas sobre un conjunto de puntos forma una teselación en capas en forma de cebolla, de utilidad para la realización de diversos análisis estadísticos sobre dichos puntos.
Círculo mínimo
El círculo mínimo es aquel circulo que contiene a todos los puntos de un conjunto dado con el menor radio posible.
El significado de este círculo mínimo es variado, ya que tanto el centro como el radio del mismo se prestan a diversas interpretaciones. Por ejemplo, si suponemos un terreno plano y una serie de núcleos de población (cada uno de ellos representado por un punto), y queremos situar una antena para dar cobertura a la región definida por esos puntos, el centro del círculo mínimo es una buena opción. Esto es así porque minimiza la distancia a la que se sitúa el punto más alejado, y por tanto minimizará la fuerza de la señal necesaria para ofrecer esa cobertura completa. La intensidad de la señal se puede calcular en función del radio del círculo.
Un análisis similar es frecuente en el terreno militar. Para un conjunto de $n$ puntos a atacar, el emplazamiento de una bomba en el centro del circulo mínimo permitirá que ese ataque afecte a todos los puntos con una cantidad mínima de explosivo. Dicha cantidad está en relación, al igual que en el caso anterior, con el radio del círculo.
La construcción de algún elemento de servicio compartido, tal como un colegio o un hospital también puede analizarse empleando el círculo mínimo. Si situamos dicho elemento en el centro, garantizamos que la distancia del usuario más lejano de dicho servicio es mínima. Cualquier otro emplazamiento implicaría que existe un usuario en peores condiciones, que tendrá que recorrer una distancia mayor para llegar a ese colegio u hospital.
Como vemos, el círculo mínimo es una herramienta útil para la localización y emplazamiento de distintos elementos. Estos problemas, no obstante, son más complejos en general, ya que implican la localización de varios elementos, o bien existen otros previos que han de considerarse, así como diversos factores externos.
Además de esta interpretación geográfica, el círculo mínimo aporta otro tipo de información. Es habitual, por ejemplo, que los puntos que se sitúan en el borde del mismo sean descartados, ya que constituyen los más alejados y en cierta medida son elementos extremos poco representativos del conjunto.
Existen muchos algoritmos para el cálculo del círculo mínimo, que escapan al ámbito de este texto. Para saber más al respecto, puede consultarse[ Megiddo1983SIAM ] o [ Skyum1991IPL ].
Es de reseñar que los punto situados en el borde del círculo mínimo siempre pertenecen a su vez a la envolvente mínima convexa. Por ello, el problema del cálculo del circulo mínimo para un conjunto de $n$ puntos puede reducirse al cálculo de dicho círculo para el subconjunto de puntos que componen la envolvente mínima convexa.
Rectángulo mínimo
El rectángulo mínimo es el rectángulo de menor área que cubre todos los puntos de un conjunto.
Pare el cálculo del rectángulo mínimo se aplica el hecho de que al menos un lado de este se sitúa sobre un lado de la envolvente mínima convexa. Por ello, basta comprobar los distintos rectángulos que pueden construirse sobre dicha envolvente, y tomar el de menor área.
Generalmente, el rectángulo de menor área coincide con el de menor perímetro, pero no siempre es así. De cualquier modo, este último también cumple la condición citada con respecto a la envolvente convexa, por lo que su cálculo puede hacerse por un procedimiento idéntico.
Generalización de líneas
Como ya sabemos, toda la información vectorial la almacenamos en ultima instancia como un conjunto de puntos, ya sean aislados o unidos mediante segmentos o curvas para conformar líneas o contornos de polígonos. Una transformación habitual en el caso de líneas o polígonos consiste en la modificación de ese conjunto de puntos de tal modo que se reduzca su número pero se preserve en la medida de lo posible la información que originalmente contenían.
Este proceso de simplificación es parte de la generalización de líneas, y es importante dentro de los Sistemas de Información Geográfica, tanto para la representación de datos como para su análisis o su simple almacenamiento, como ya vimos al inicio de este libro.
Las razones por las cuales puede resultar de interés llevar a cabo un proceso de generalización de líneas son diversas, y entre ellas cabe destacar las dos siguientes [ McMaster1992AAG ].
- Reducción del tamaño de los datos . Una reducción del número de puntos elimina puntos en muchos casos superfluos, de tal forma que la capa simplificada presenta la misma utilidad pero ocupa un espacio menor.
- Reducción del tiempo de proceso . La capa generalizada se maneja de forma más rápida en operaciones tales como la representación en pantalla, la impresión, o la realización de otros cálculos. En términos generales, todos los cálculos con la línea generalizada, como por ejemplo el trazado de una zona de influencia o de cualquier otro de los procesos vistos en este capítulo, se efectúan con un menor costo de proceso, ya que requieren el análisis de un menor número de puntos. Otros procesos tales como la conversión de esa capa en una capa ráster también experimentan una ganancia en rendimiento.
En ocasiones, la simplificación puede implicar la reducción de elementos más allá de puntos aislados, tal y como operan los algoritmos que a continuación veremos. Eliminando puntos a lo largo de una línea puede lograrse el resultado buscado, reduciendo el detalle longitudinalmente, pero un cambio de escala puede también implicar la necesidad de eliminar no únicamente puntos, sino líneas completas. Por ejemplo, si una capa de líneas recoge con detalle una vía mediante dos líneas, una para cada borde de la misma, no tiene sentido emplear una capa de tal detalle para un mapa a una escala tal como, por ejemplo, 1:200000. En este caso, puede sustituirse el par de líneas anteriores por una única, ya que la variación en el resultado no será perceptible. La simplificación de las líneas en este caso debe operar sustituyendo dos líneas por una única.
Si esa carretera queda recogida mediante un polígono, puede simplificarse mediante un proceso de «adelgazamiento» que convierta este en una línea central. La obtención de este eje del polígono se hace con un proceso que es similar a la zona de influencia hacia el interior de un polígono, la cual veíamos al principio de este mismo capítulo.
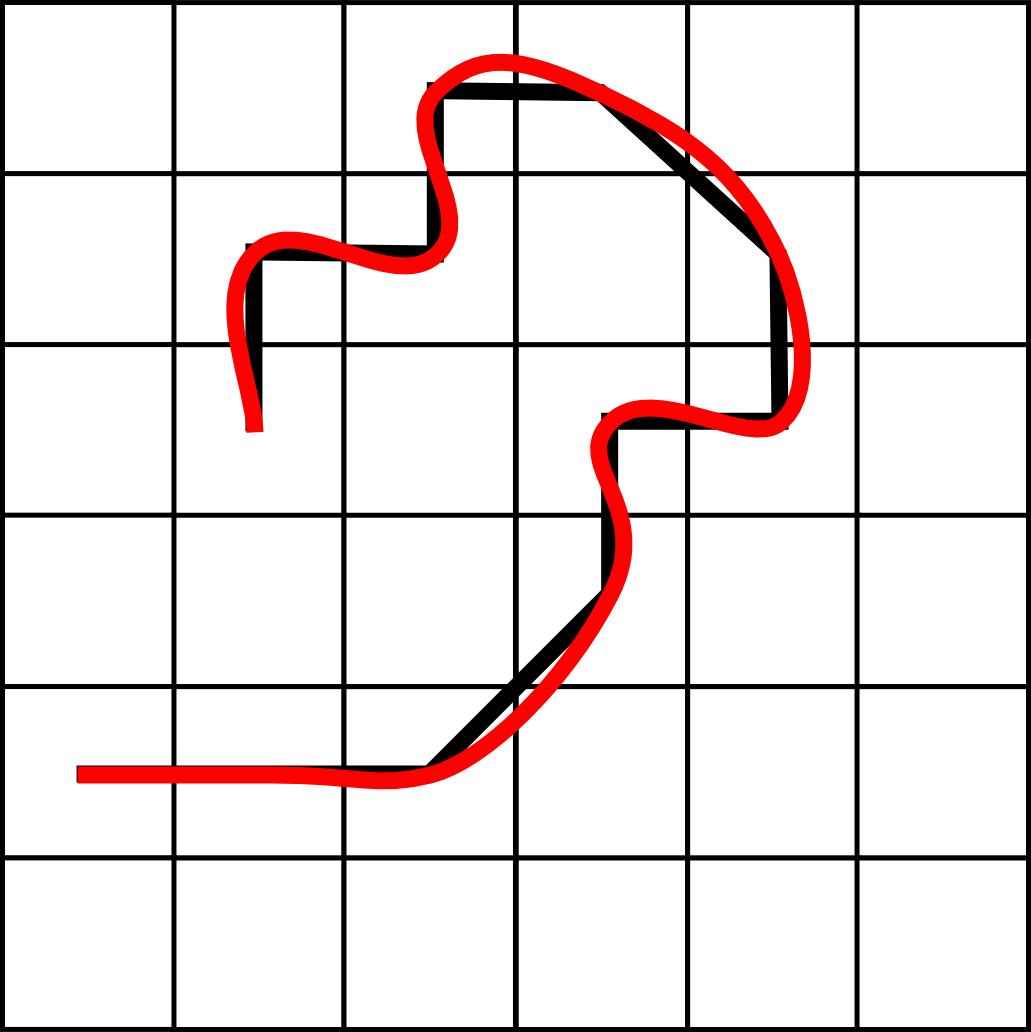
Una operación también relacionada con la generalización de líneas es el suavizado . En muchas ocasiones, las líneas de una capa vectorial son excesivamente angulosas y no presentan un aspecto natural, muy distinto del trazo suave con que un cartógrafo trazaría estas al realizar un mapa. Alterando el conjunto de puntos de la línea de forma similar a lo visto anteriormente, puede lograrse un redondeo en las curvas definidas por este. Dicho redondeo puede buscarse con meros fines estéticos, pero también para eliminar variaciones bruscas o desviaciones locales, manteniendo tan solo la forma general de la linea. Este es, por ejemplo, el proceso que debe realizarse si deseamos utilizar las líneas a una escala de menor detalle que la que originalmente se empleó en su creación.
El suavizado de líneas es también útil como preparación de datos de líneas procedentes de un proceso de digitalización. Aunque muchos elementos naturales tienen formas redondeadas, es habitual que la digitalización genere elementos más angulosos que el objeto real que se digitaliza.
Algo similar sucede cuando las operaciones de vectorización se realizan de forma automática, tales como las que vimos en en capítulo Creacion_capas_vectoriales . El suavizado de las líneas mejora en tal caso la calidad de estas, no solo en su aspecto estético, sino también en su similitud con el objeto modelizado, ya que se trata de formas más naturales(Figura \ref{Fig:Suavizar_digitalizado}).
Métodos
Los algoritmos para la generalización de líneas son muy diversos y tienen cada uno sus propias características de precisión y rendimiento. La forma más simple de generalización consiste sencillamente en eliminar puntos sin considerar la relevancia de estos dentro de la línea. Esta eliminación puede realizarse de forma sistemática (eliminar un punto de cada $n$), o bien aleatoria. La magnitud del proceso de generalización se mide por el número total de puntos eliminados.
No obstante, no todos los puntos de un línea tienen la misma importancia y aportan la misma cantidad de información. Algunos puntos pueden resultar redundantes, mientras que otros pueden ser cruciales para la forma del trazado. Como puede verse en la figura \ref{Fig:Simplificacion_importancia_ptos}, eliminar algunos puntos puede no tener apenas efectos sobre la línea original o bien resultar en una variación drástica de su forma. Un mismo número de puntos eliminados puede dar lugar a líneas muy similares o muy distintas a la original, según sea el caso, por lo que esta medida de la simplificación no es una medida de cuan fidedigna es la línea resultante.
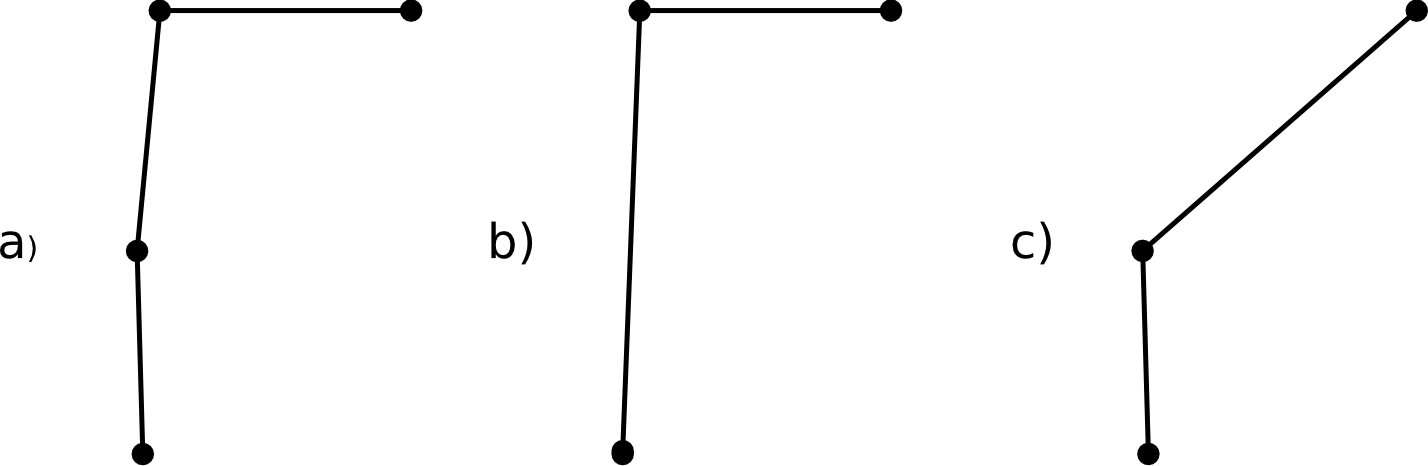
Puesto que no todos los puntos deben ser considerados de igual modo, existen métodos de simplificación que consideran la naturaleza propia del punto dentro de la línea y estudian esta como entidad en su conjunto. Esto garantiza resultados mejores que con la mera eliminación sistemática de puntos intermedios.
Podemos clasificar las rutinas de generalización de líneas en los siguientes bloques [ McMaster1987Cartographica ].
- Rutinas de vecindad inmediata . Analizan cada punto y los inmediatamente anteriores y posteriores, estudiando los ángulos formados o las distancias.
- Rutinas de vecindad acotada . Estudian una serie de puntos vecinos, no necesariamente restringida a los inmediatos pero sí con algún umbral máximo de alejamiento o número de puntos.
- Rutinas de vecindad no acotada . Estudian los puntos vecinos y la región analizada depende de diversos factores, aunque no existe una dimensión máxima.
- Rutinas globales . Analizan la línea de forma global.
- Rutinas que preservan la topología . Además de las propiedades geométricas, ya sea a nivel global o local, estudian la conectividad y topología del conjunto de líneas para garantizar que la línea simplificada preserva dichas propiedades.
Uno de los algoritmos más habitualmente utilizados es el propuesto por[ Douglas1973TAC ], que pertenece al grupo de los globales. La intensidad del proceso de generalización se establece mediante un valor de tolerancia que indica la máxima desviación que se permite entre la línea original y la simplificada.
En la figura \ref{Fig:Generalizacion} puede verse cómo una línea original se simplifica de diversas formas al aplicar tolerancias crecientes con este algoritmo.

Respecto a los algoritmos de suavizado, estos pueden dividirse en tres grupos principales [ McMaster1987Cartographica ]:
- Media entre puntos . Se consideran un número $n$ de puntos vecinos, y en base a ellos se calcula la nueva posición.
- Ajuste de funciones matemáticas . Ajustando a los puntos funciones que tengan un aspecto «suave», tales como splines o curvas Bézier.
- Tolerancias . Se establece una tolerancia y un umbral de precisión, y se ignoran los detalles a lo largo de la línea que salen de ese umbral.
En [ McMaster1989Cartographica ] pueden encontrarse detallados métodos de todas las familias anteriores.
Resumen
Las operaciones geométricas sobre entidades vectoriales constituyen en cierta forma el equivalente del álgebra de mapas ráster sobre las capas vectoriales.
Las operaciones más importantes son el cálculo de zonas de influencia y las denominadas operaciones de solape, que permiten combinar capas de diversas maneras. Entre estas encontramos las operaciones de intersección, unión, diferencia y recorte, así como el juntado de capas. Las tablas de valores asociadas a las capas resultantes de estos procesos deben considerarse y tratarse con precaución, ya que las transformaciones que se realizan sobre las geometrías pueden afectar a la validez de los datos que contienen.
Las tablas pueden también usarse para definir otro tipo de operaciones tales como la disolución, en la que se unen regiones que comparten algún atributo común.
Por último, las operaciones de generalización de líneas son útiles para disminuir el tamaño de los datos vectoriales, con las ventajas de manejo y proceso que ello conlleva.