Más estadística espacial

Introducción

Prácticamente todas las formulaciones estadísticas pueden aplicarse a datos geográficos de igual forma que se aplican a datos de otro tipo. No obstante, la particular naturaleza de la información geográfica hace que algunas de estas formulaciones puedan adaptarse de forma específica para obtener resultados más correctos. En particular, la inferencia estadística presenta, como ya vimos, una serie de peculiaridades que hacen conveniente su adaptación para considerar la especial naturaleza debida a la presencia de una componente espacial.

En este capítulo, intentaremos profundizar algo más sobre el empleo de estas herramientas estadísticas dentro del ámbito de un SIG, viendo, entre otros, los métodos de regresión que consideran explícitamente la componente espacial de los datos, así como las metodologías que constituyen la base para la creación de modelos predictivos, de gran aplicación dentro de los SIG.

Asimismo, existe una operación estadística con un particular peso dentro del ámbito del SIG: la clasificación, la cual constituye un elemento básico especialmente en el tratamiento de imágenes y la creación de datos espaciales de carácter temático a partir de estas. Dedicaremos gran parte del capítulo a detallar los pormenores del proceso de clasificación y algunas, las más populares, de sus muy diversas variantes.

Ya conocemos algunas formulaciones que nos permiten, a partir de una capa ráster (sea una imagen o no), obtener capas vectoriales o nuevas capas ráster de variable discreta, conteniendo una información adecuada para ser expresada en formato vectorial, de forma similar a las operaciones de clasificación. El capítulo dedicado al procesado de imágenes contenía algunas de estas formulaciones, basadas en aquel caso en operaciones con apenas componente estadística. Los procesos de clasificación de este capítulo abordan, como hemos dicho, una tarea similar, pero desde un enfoque principalmente estadístico.

El Análisis de Componentes Principales , otra técnica estadística habitual, también es de gran utilidad en el trabajo con imágenes, especialmente cuando estas contienen un gran número de bandas. La redundancia que aparece en estas imágenes al existir dependencia entre sus bandas puede eliminarse aplicando esta técnica, al igual que cuando se trabaja con cualquier otro conjunto de múltiples capas, cada una de ellas referida a una variable distinta.

Por último, cerraremos el capítulo presentando algunas metodologías que nos ayudaran a extender las capacidades de las operaciones locales del álgebra de mapas, es decir, aquellas que empleábamos para combinar una serie de capas ráster. Las operaciones algebraicas que utilizamos para efectuar dicha combinación de capas pueden mejorarse si se aplica un análisis estadístico de las distintas variables combinadas, dando esto lugar a metodologías más avanzadas.

Clasificación

La clasificación es una operación muy habitual dentro del análisis SIG, pues permite establecer una categorización de un área de estudio a partir de una serie de variables, con la utilidad que ello conlleva para otros análisis. Esencialmente, el proceso de clasificación convierte una serie de capas en otra única con información categórica. Las capas de origen suelen contener en general variables de tipo continuo, aunque no necesariamente. Se trata de, en función de la información disponible sobre un área geográfica, clasificar de acuerdo con algún criterio las distintas zonas de la misma.

Esta clasificación se desarrolla mediante procedimientos diversos que evalúan a cuál de las clases posibles es más similar un punto dado. En dicho punto, se toman los valores de todas las variables registradas y ese conjunto de valores es el utilizado para calcular el grado de similitud entre la clase presente en el punto (aún no determinada) y las distintas clases posibles.

Dos circunstancias son de reseñar en relación con la naturaleza de las capas de partida:

• Por tratarse de variables continuas en la mayoría de los casos, se suele trabajar principalmente con capas ráster como capas de origen.
• Por utilizarse en general más de una variable, se requieren varias capas para almacenar estas.

Como ya vimos, la estructura de las imágenes procedentes de teledetección, en formato ráster y con múltiples bandas, las hace ideales para ser utilizadas como datos de partida para obtener capas clasificadas. Por esta razón, es frecuente ver los algoritmos de clasificación tratados en textos dedicados al análisis de imágenes, o bien en las partes sobre imágenes de los textos genéricos sobre SIG. No obstante, no deben entenderse como limitados a este tipo de datos, ya que resultan igualmente de utilidad aplicados sobre cualquier conjunto de capas ráster, sin que estas sean bandas de una imagen o sin que las variables empleadas hayan sido recogidas por un mismo instrumento o sensor.

Un número dado de valores recogidos en otras tantas bandas de una imagen sirven para evaluar, por ejemplo, el tipo de material del que se compone un suelo, puesto que las distintas clases establecidas en función de esos materiales guardan relación con las intensidades a distintas longitudes de onda que dicho suelo refleja. Pero del mismo modo, y como ya se comentó en Caracterizacion_terreno , las formas del relieve también pueden dividirse en clases atendiendo a la pendiente, la curvatura o el índice de humedad topográfica, entre otros parámetros. Y de manera similar, establecer una caracterización de las distintas zonas puede llevarse a cabo a partir de valores de pH del suelo, pendiente o humedad, por nombrar algunos.

Incluso pueden combinarse bandas procedentes de imágenes y otro tipo de variables. Por ejemplo, al clasificar las distintas zonas de vegetación a partir de una imagen, pueden añadirse valores de pendiente o elevación, ya que estos parámetros del terreno tienen una obvia relación con la vegetación existente.

Como veíamos en el capítulo sobre imágenes, el conjunto de valores de las distintas bandas de una imagen en un punto constituía lo que denominábamos firma espectral . Al trabajar con otro tipo de variables, el conjunto de valores en un punto que empleamos para clasificarlo ya no recibe ese nombre, que es propio del análisis de imágenes, pero el concepto sigue siendo, sin embargo, el mismo.

En el caso de imágenes, la clasificación es, además de una técnica estadística, un proceso con una base física, pues pueden estudiarse directamente los valores de radiación reflejada a distintas longitudes de onda y adjudicarles un significado en función de lo que dichas longitudes de onda condiciones. En otros ejemplos, sin embargo, se trata de un proceso meramente estadístico. Esta componente estadística y su formulación será lo que veamos en este apartado.

La clasificación, pues, puede definirse como el proceso que, dados un conjunto de elementos (en este caso, localizaciones espaciales) las agrupa en una serie de clases de forma que estas sean homogéneas en cuanto a las características de los elementos que contienen.

Este proceso conlleva dos etapas:

• Definición de las clases
• Asignación de cada elemento a una de dichas clases

En función de cómo se lleve a cabo la definición de las clases, los métodos de clasificación pueden dividirse en dos grupos principales:

• Clasificación supervisada. Además de emplear las capas como entrada, debe añadirse información adicional que ayude en la definición de las distintas clases, definiendo el número de estas y sus características.
• Clasificación no supervisada. La única entrada son las capas y el número de clases a definir. Las características de dichas clases se establecen en función del conjunto de valores con los que se trabaja.

Clasificación supervisada

La clasificación supervisada es una forma de clasificación que requiere por parte del operador la definición explicita de las clases a definir. En la terminología empleada para las imágenes, podemos decir que el operador debe introducir la firma espectral característica de las clases, expresada esta como los valores más habituales que aparecen para dicha clase. El proceso de clasificación asigna a un punto aquella clase cuyo conjunto de valores «típicos» de las variables estudiadas (los que vienen definidos por esa firma espectral característica) son más similares a los presentes en dicho punto.

La figura \ref{Fig:Esquema_clasificacion_supervisada} muestra un esquema de este proceso.

$$\label{Fig:Esquema_clasificacion_supervisada}$$

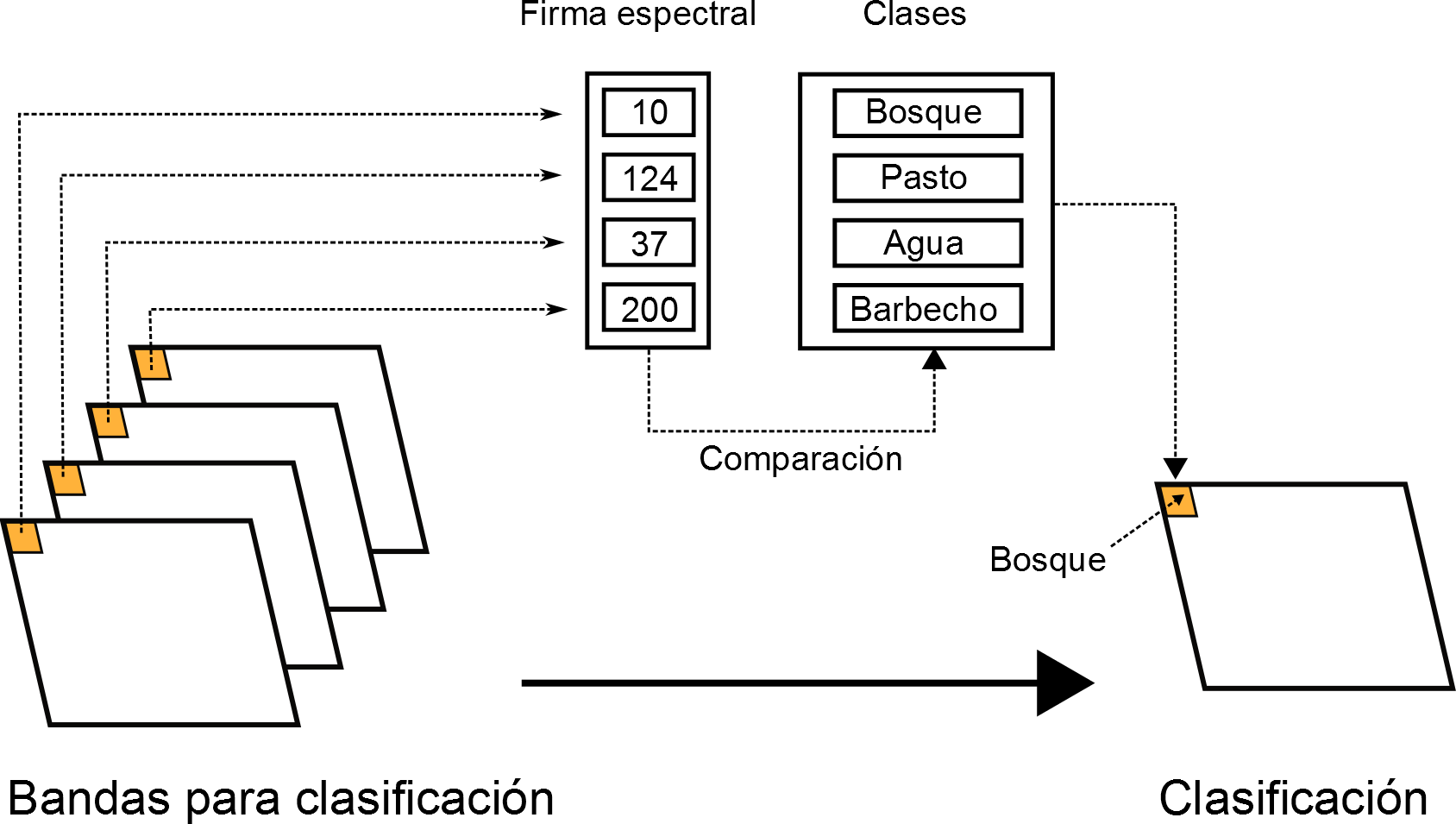
La forma en que pueden proporcionarse definiciones de clase a un método de clasificación supervisada son dos:

• Mediante zonas de entrenamiento
• Mediante valores directos

Al utilizar zonas de entrenamiento, el operador debe delimitar algunas zonas en las que se conozca a priori el tipo de clase existente. Esto puede hacerse con una capa de polígonos adicional que tenga asociado en un campo de su tabla de atributos el tipo de clase presente en dicho polígono. El algoritmo de clasificación, en su primera fase, estudiará las celdas de las capas de entrada que caen dentro de los polígonos de cada clase, y con sus valores tratará de definir los rasgos generales de esas clases que permitirán identificar clases similares en otros puntos.

A la hora de definir estas zonas de entrenamiento, debe procurarse que cubran toda la casuística de las clases que definen. Si, por ejemplo, queremos clasificar un área de estudio en tres simples clases como «bosque», «cultivo» y «carretera», y las zonas de bosque son heterogéneas (distintas especies, distinta densidad, etc.), será conveniente definir zonas de entrenamiento en distintos tipos de bosque, para que puedan extraerse las características comunes a todas las subtipologías que vamos a englobar en una única clase.

Por supuesto, si queremos definir una clase concreta, debemos establecer una o varias zonas de entrenamiento de esta. Es decir, el algoritmo solo clasifica en los grupos que el operador haya definido. Si en el área de estudio mencionada anteriormente existieran zonas en barbecho (que no pertenecen a ninguna de las tres clases señaladas), estas no van a asignarse a una clase nueva. En función de la metodología que posteriormente se use para dicha asignación, o bien quedarán sin clasificar (si son muy distintas sus características de las de todas las clases establecidas), o bien quedarán englobadas dentro de la clase con la cual presenten una mayor similitud (que probablemente, y pese a ser la más similar de las tres definidas, no sea muy parecida a la realidad).

Para obtener mejores resultados, las zonas de entrenamiento deben ser lo más representativas posibles, y deben establecerse siempre que se tenga la seguridad de que efectivamente pertenecen a la clase a definir. Un mayor número de zonas de entrenamiento implica mejor clasificación en líneas generales, pero solo si estas zonas constituyen una definición coherente de la clase, y no si se emplean zonas cuya tipología no se conozca con plena certeza.

Cuanto más grandes sean las zonas de entrenamiento, más celdas contendrán en las capas de variables analizadas, y más precisa sera la definición de las características de cada clase. [ Swain1978McGraw ] recomienda que se tomen para cada clase al menos un número de celdas diez veces superior al de variables consideradas, siendo más adecuado que este sea cien veces mayor.

Además de emplear zonas de entrenamiento, la otra forma de comunicarle al algoritmo de clasificación qué clases queremos definir y qué características tienen estas es mediante valores directos. En el análisis de las zonas de entrenamiento, las zonas se caracterizan según unos valores estadísticos tales como la media y la desviación típica de las distintas variables empleadas. Si ya hemos realizado ese proceso anteriormente, dichos valores ya han sido calculados, y podemos utilizarlos para alimentar un nuevo proceso de clasificación en otro área de estudio. Lógicamente, esto es posible solo si las clases a definir tienen características similares en este nuevo área y en la utilizada originalmente para la caracterización de clases.

La utilización de valores provenientes de bases de datos de firmas espectrales, las cuales se vieron en el capítulo Procesado_imagenes , constituye otro ejemplo del uso de valores directos en lugar de zonas de entrenamiento.

Una vez que las clases se han definido, el proceso de clasificación asocia cada punto de la zona de estudio a una de ellas en función de sus valores. Los métodos existentes para llevar a cabo esta fase del proceso son muy diversos, y la literatura estadística recoge decenas de ellos. Dentro del ámbito de los SIG, los más habituales son los siguientes:

• Clasificación por paralelepípedos.
• Clasificación por mínima distancia.
• Clasificación por máxima verosimilitud.

Se trata de métodos sencillos en su mayoría, existiendo formulaciones más complejas y avanzadas que, no obstante, resulta menos frecuente encontrar implementadas en un SIG. Algunos de estos métodos que merecen ser mencionados son los basados en redes neuronales, árboles de decisión o sistemas expertos. La ventaja frente a los anteriores es que no asumen una distribución estadística particular de los datos, y pueden aplicarse aun en el caso de que dicha distribución no se dé.

Para más información, pueden consultarse, entre otras referencias, [ Bendiktsson1990IEEE ], [ Bosch1999GeoComputation ], [ Hepner1990PERS ] y [ Paola1995IEEE ]. Métodos basados en lógica difusa se recogen, por ejemplo, en [ Foody1996IJRS ]. Todas estas metodologías se presentan generalmente aplicadas a la clasificación de imágenes, aunque una vez más su uso no se ha de restringir al caso particular de estas.

Antes de aplicar cualquiera de estos métodos o los que seguidamente veremos con detalle, puede resultar recomendable homogeneizar los rangos de las distintas variables. En el caso de emplear únicamente imágenes, los Niveles Digitales de estas se encuentran siempre en el mismo rango (0--255), pero este puede ser más heterogéneo si se usan capas con otro tipo de variables. Un proceso de normalización (lo vimos en Funciones_locales ) es una opción habitual en este caso, empleándose como preparación previa al análisis y la clasificación.

Paralelepípedos

El método de clasificación por paralelepípedos establece regiones, una por cada clase, con dicha forma de paralelepípedos dentro del espacio de atributos en el que se trabaja. La pertenencia de una localización a una de las clases se establece viendo si la posición que sus valores definen en el espacio de atributos está dentro de la región correspondiente a la clase.

Los distintos lados de los paralelepípedos vienen definidos por la media de cada variable en la clase y su desviación típica. La longitud de los lados es igual a dos veces la desviación típica, y se encuentran centrados en la media. Un esquema de esto puede verse en la figura \ref{Fig:Paralelepipedos}. Los puntos representados son elementos que se quieren clasificar, que en el caso de una capa ráster serán mucho más numerosos, uno por cada celda. Por simplicidad de representación y visualización, se supone en dicha figura, así como en las siguientes correspondientes a otros métodos, que se utilizan dos variables para efectuar la clasificación (por tanto, es un gráfico bidimensional), y se definen tres únicas clases. El mismo tipo de análisis puede, no obstante, aplicarse a cualquier numero $n$ de variables (resultaría un espacio de atributos n--dimensional) y, por supuesto, cualquier número de clases.

$$\label{Fig:Paralelepipedos}$$

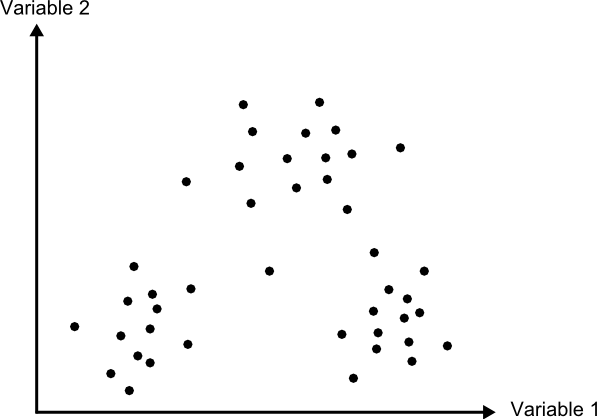
Una característica de este método es que pueden existir elementos que no puedan ser clasificados, al no caer dentro de ningún paralelepípedo. Del mismo modo, estos pueden solaparse y ciertos elementos pueden pertenecer simultáneamente a varias clases. En caso de darse esta circunstancia, puede resolverse aplicando alguno de los otros métodos, tal como el de máxima verosimilitud.

En general, la precisión de este método es baja, y el número de elementos sin clasificar o clasificados en varias categorías es alto. Su mayor ventaja reside no en su exactitud, sino en la velocidad de proceso, al no requerir operaciones complejas.

Mínima distancia

El método de mínima distancia se basa también en conceptos geométricos dentro del espacio de atributos. En este caso se emplea únicamente la media de cada clase, prescindiéndose de la desviación típica.

Para cada uno de los elementos a clasificar se calcula la distancia euclídea en el espacio de atributos entre la media de cada clase y dicho elemento. Esta distancia viene expresada por

\begin{equation} d_k = \sqrt{(x_i - \overline{x}_{ik})^2} \end{equation}

siendo $d_k$ la distancia del elemento al centro de la clase k-ésima, $x_i$ el valor asociado al elemento para la variable i-ésima, y $\overline{x}_{ik}$ la media de los valores de la clase k-ésima para la variable i-ésima.

Aquella clase hasta la que exista una menor distancia será a la que se asigne el elemento en cuestión.

En lugar de emplear distancia euclídea puede utilizarse la distancia de Manhattan, ya que disminuye el número de operaciones (lo cual implica más velocidad de proceso).

Puede verse que esta metodología guarda similitud conceptual con la interpolación por vecindad, en la que asignábamos el valor del punto más cercano. En la figura \ref{Fig:Minima_distancia} puede verse un gráfico explicativo de este método de clasificación.

$$\label{Fig:Minima_distancia}$$

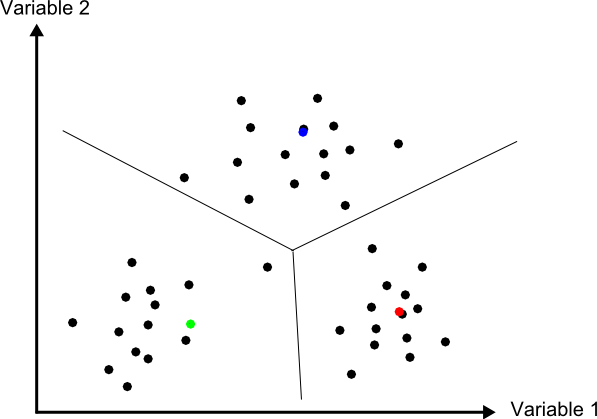
A diferencia del método anterior, todos los elementos pueden clasificarse, ya que siempre existe uno más cercano. Esto constituye una de las potenciales desventajas del método, ya que puede hacer asignaciones incorrectas en el caso de que un elemento sea muy distinto a todas las clases de partida. Se asignará a la clase más similar, lo cual no significa necesariamente que sea lo suficientemente similar a ella como para considerarlo parte de la misma.

Por ejemplo, y repitiendo un ejemplo ya citado, si tenemos las clases «bosque», «cultivo» y «carretera», y en nuestro área de estudio existe una zona en barbecho, esta será clasificada dentro de alguno de los grupos anteriores, que puede ser uno u otro en función de los datos que empleemos para la clasificación. Con independencia de cuál sea esa clase escogida, resulta claro que sera una asignación errónea, y que o bien debería haberse incorporado esta clase dentro de las zonas de entrenamiento, o bien toda esa zona de barbecho debería quedar sin clasificar.

Un método similar al de mínima distancia es el basado en distancia de Mahalanobis.

La distancia euclídea puede expresarse de forma matricial como

\begin{equation} d_k = \sqrt{(X-\overline{X}_k)^T(X-\overline{X}_k)} \end{equation}

donde $X$ y $\overline{X}_k$ son respectivamente los vectores de valores del elemento a clasificar y de valores medios de la clase k--ésima.

La distancia de Mahalanobis es una generalización de esta, y en su forma matricial tiene la siguiente expresión:

\begin{equation} d_k = \sqrt{(X-\overline{X}_k)^TC^{-1}(X-\overline{X}_k)} \end{equation}

donde $C$ es la matriz de covarianzas entre las variables estudiadas. Es decir, una matriz de la forma

\begin{equation} \label{Eq:Matriz_covarianzas} C = \left( \begin{array}{cccc} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1n} \\ \sigma_{21} & \sigma_{22} & \cdots & \sigma_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{n1} & \sigma_{n2} & \cdots & \sigma_{nn} \\ \end{array} \right) \end{equation}

donde $\sigma_{ij}$ es la covarianza entre las variables $i$ y $j$.

Máxima verosimilitud

A diferencia de los anteriores, el método de máxima verosimilitud no evalúa un parámetro geométrico dentro del espacio de atributos, sino que se basa en fundamentos estadísticos. Conociendo la media y desviación típica que caracteriza a una clase, podemos suponer una función de densidad de probabilidad, y con los valores de un elemento dado estimar la probabilidad de que estos correspondan a cada clase. La clase con una mayor probabilidad es aquella a la que se asigna el elemento.

Este método comparte con el de distancia mínima el hecho de que todos los elementos quedan clasificados. No obstante, resulta sencillo aplicar un umbral inferior a los valores de probabilidad, de tal forma que si la clase más probable tiene un valor por debajo del umbral no se asigne el elemento a dicha clase. En este caso el método es en cierta medida semejante al de paralelepípedos, pero en lugar de estos se tienen hiperelipses n-dimensionales. Puede darse igualmente el caso de que un elemento se encuentre dentro de varias de estas hiperelipses, el cual se resuelve directamente con los valores de probabilidad de estas.

Puede verse un gráfico relativo a este método en la figura \ref{Fig:Maxima_verosimilitud}, considerando la aplicación de un umbral inferior de probabilidad.

$$\label{Fig:Maxima_verosimilitud}$$

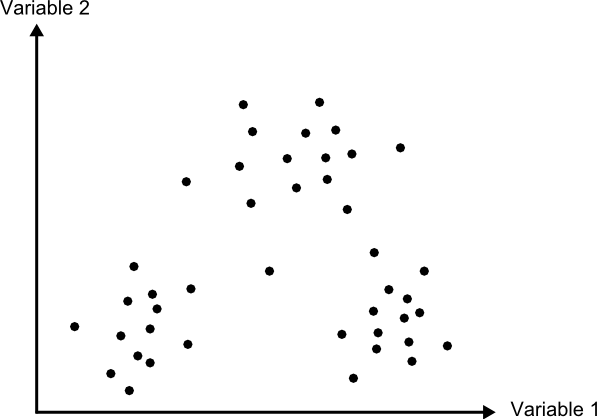
Es importante recalcar que al emplear este método se asume que los datos tienen una distribución normal, lo cual no ha de ser necesariamente cierto según qué tipo de variables manejemos. Es importante tener en cuenta este hecho antes de utilizar este clasificador sobre nuestros datos.

Clasificación no supervisada

Los métodos de clasificación no supervisada no requieren del operador la definición explícita de las clases. No es necesario ningún conocimiento a priori , ya que es el propio algoritmo quien las define de acuerdo a los datos. Para llevar esto a cabo, es necesario suministrar algunos valores tales como el número de clases que se desea crear, los tamaños mínimos y máximos de cada una, o ciertas tolerancias para la distinción entre clases. Estos parámetros «guían» al algoritmo en la definición de clases, que se produce en estos métodos de forma simultanea a la asignación de los elementos a una u otra de dichas clases.

En general, se trata de procedimientos iterativos en los que una clasificación inicial va convergiendo hacia una final en la cual se cumplen las características buscadas de homogeneidad, número de clases, etc.

Por su propia naturaleza, estos métodos no generan clases de las cuales se conoce su significado, y será necesario estudiarlas después para saber qué representa cada una de ellas. Si en un método de clasificación supervisada definimos zonas de entrenamiento con distintas clases de suelo, el resultado sera una capa dichas con clases de suelo. Si diferenciamos según otro criterio, será ese criterio el que quede reflejado en la capa resultante. En el caso de la clasificación no supervisada, no existe tal criterio, ya que simplemente se aplican meras operaciones estadísticas con los datos, pero no se trabaja con el significado de estos. Al utilizar una zona de entrenamiento sí estamos empleando este significado, ya que le estamos diciendo al algoritmo que los valores de dicha zona representan una clase dada, esto es, que «significan» dicha clase.

Junto a la capa de clases resultantes, los métodos de clasificación no supervisada proporcionan una definición de dichas clases a través de los valores estadísticos de las mismas. Estos valores se emplearán para asignar una interpretación a cada clase una vez estas hayan sido definidas. Junto a ellas, es habitual añadir la varianza de cada clase, como indicador de la homogeneidad lograda en la clasificación.

Aunque los métodos de clasificación no supervisada son validos de por sí para establecer una separación categórica dentro de un área de estudio, es habitual que se empleen como soporte a métodos de clasificación supervisada. Mediante estos métodos se obtiene una primera división, que puede utilizarse posteriormente bien sea para la definición de zonas de entrenamiento o bien para operaciones más complejas como la clasificación basada en objetos que veremos más adelante.

Al igual que sucedía en el caso supervisado, existen numerosos métodos de clasificación no supervisada. La literatura estadística es rica en este tipo de formulaciones, conocidos como métodos de clustering , siendo dos de los más habituales dentro del ámbito de los Sistemas de Información geográfica los siguientes:

• Distancia mínima iterativa
• ISODATA

Distancia mínima iterativa

El método de distancia mínima iterativa [ Forgy1965Biometrics ] se basa en un proceso iterativo en el cual, a partir de unas clases iniciales definidas arbitrariamente, se asignan los distintos elementos a estas mediante un método de los vistos en el apartado anterior, particularmente el de distancia mínima. El número de clases iniciales es definido por el operador, y será el que aparezca en la capa resultante. Para aplicar la clasificación por distancia mínima solo es necesario conocer los valores medios de las clases, siendo este el único estadístico de cada clase con el que se va a trabajar.

Una vez que se ha realizado la asignación de clases en la primera iteración, se estudian los puntos que están incluidos en cada clase y se calculan nuevamente los valores de las medias por clase. Es decir, las clases resultantes del proceso anterior son utilizadas en cierto modo como zonas de entrenamiento. Con estos nuevos valores calculados de las medias, se vuelve a repetir la fase de asignación por distancia mínima, y así sucesivamente hasta que se cumple un criterio de convergencia.

En cada iteración del proceso hay elementos (celdas en nuestro caso, puesto que trabajamos con capas ráster) que cambian de clase. El número de dichos elementos que varían su clase se emplea como criterio de convergencia, estableciéndose un umbral inferior. Si en una iteración el número de elementos que varían es menor que el umbral, se considera que el proceso ha convergido, y se detiene su ejecución. La varianza media de las clases puede utilizarse también como medida de la modificación que se produce entre el resultado de una iteración y el de la anterior. Si no se produce una disminución suficiente de la varianza, las iteraciones ya no mejoran la clasificación obtenida, con lo cual puede asumirse que el proceso ha convergido a un resultado óptimo.

El operador especifica dicho umbral de convergencia junto al número de clases deseadas, y habitualmente también un número máximo de iteraciones, con objeto de detener el proceso en caso de que no se alcance la convergencia especificada.

Este algoritmo, así como el que veremos seguidamente, clasifica todos los elementos en algún grupo, no existiendo la posibilidad de tener una capa resultante en la que existan celdas sin clasificar. De hecho, todas las celdas son utilizadas para la definición de las medias de clases sucesivas, por lo que puede decirse que todas influyen sobre la clasificación de las restantes y al final del proceso estarán asignadas siempre a alguna clase.

Como es fácil intuir, los valores iniciales de las medias de clase condicionan el proceso de clasificación, influyendo sobre la rapidez con que este converge y también sobre el resultado. Una solución habitual para establecer estos centros de clase es hacerlo equiespaciadamente en el rango que los valores a clasificar cubren dentro del espacio de atributos.

En la figura \ref{Fig:Clases_iniciales_isoclusters} puede verse gráficamente la forma de definir estas clases iniciales. Sobre la diagonal que atraviesa el espacio de atributos se establecen tantos puntos como clases quieran definirse. Estos serán los valores medios a los que se calculen las distancias desde cada elemento en la primera iteración.

$$\label{Fig:Clases_iniciales_isoclusters}$$

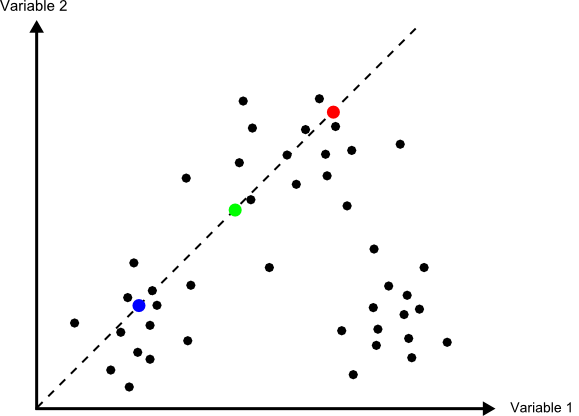
Como puede verse, los centros de las clases no se corresponden con los centros de los grupos que existen en el conjunto de elementos, pero al cubrir el espacio y repartirse a lo largo de este, garantizan que en las sucesivas iteraciones estos centros puedan desplazarse al lugar correcto donde las clases que definan presenten una mínima variabilidad.

En la figura \ref{Fig:Etapas_clustering} pueden verse algunas etapas de un proceso de clasificación no supervisada por el método de distancia mínima iterativa, en el que se aprecian los cambios que las clases van sufriendo a lo largo de las sucesivas iteraciones.

$$\label{Fig:Etapas_clustering}$$

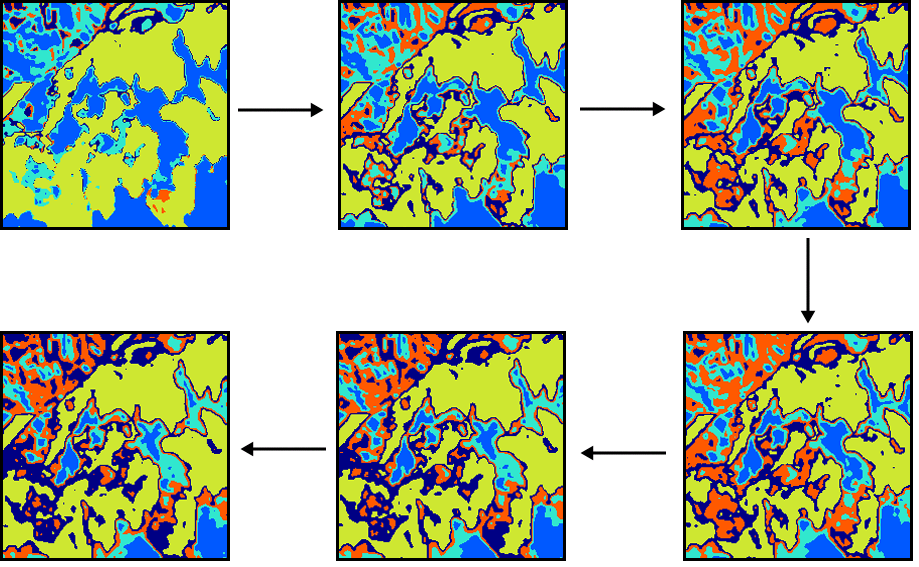
ISODATA

El método ISODATA (Iterative Self-Organizing Data Analysis Technique) comparte los mismos fundamentos que el anterior, pero le añade algunos elementos adicionales que permiten al operador tener algo más de control sobre el proceso, al tiempo que aportan una mayor flexibilidad a los resultados.

Por una parte, puede darse el caso en que algunas de las clases establecidas no tengan suficientes elementos asignados a ellas, y no sea relevante mantenerlas. Los elementos de estas clases pueden asignarse a la siguiente clase más cercana. El método ISODATA analiza la capa resultante en busca de clases con pocos elementos, y en caso de que no superen un umbral mínimo de número de estos, los reparte entre las restantes clases. Mediante esta operación, el número de clases totales disminuye en uno.

Otro caso similar se da cuando dos de las clases resultantes son muy similares, existiendo poca distancia entre sus medias respectivas. En este caso, resulta conveniente unir dichas clases. La definición de un umbral mínimo de distancia entre clases permite al algoritmo considerar esta circunstancia.

Un caso opuesto a los anteriores se da cuando una clase tiene una amplitud excesiva, de tal modo que la variabilidad en ella sea elevada. Puede establecerse un umbral de amplitud en función de la desviación típica, que permita localizar dichas clases, para posteriormente dividir estas en dos nuevas.

Con todo lo anterior, además de especificarse un número de clases a crear se establece un número máximo y otro mínimo de clases, para de este modo acotar el número de clases totales que resulta de los procesos de ajuste mencionados. Incluyendo estos procesos junto a la estructura del algoritmo de distancia mínima iterativa, se tiene el proceso global del método ISODATA.

Como conclusión de esta sección dedicada a la clasificación y los métodos existentes, en la figura \ref{Fig:Comparacion_metodos_clasificacion} se muestra un ejemplo de clasificación de usos de suelo en un área de estudio, en base a imágenes de satélite y parámetros fisiográficos, llevada a cabo por algunos de los métodos descritos anteriormente.

$$\label{Fig:Comparacion_metodos_clasificacion}$$

Clustering jerárquico

Un algoritmo habitual en clasificación de objetos es la utilización de árboles jerárquicos. El proceso se basa en la creación de un árbol en el cual se disponen en sus extremos todos los objetos a clasificar, y las ramas que estos conforman se van unificando, agrupándose por similitud hasta llegar a formar una única (Figura \ref{Fig:Clustering_jerarquico})

$$\label{Fig:Clustering_jerarquico}$$

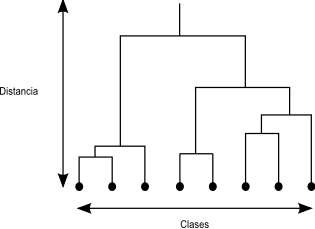
El dendrograma resultante de este proceso puede utilizarse después para clasificar los elementos, simplemente descendiendo en él hasta el nivel en el que el número de clases existentes sea lo más cercano posible al deseado. Este dendrograma es más rico en información que la mera clasificación, ya que presenta distintos niveles de agrupación en lugar de uno único.

El problema con este tipo de métodos para su uso en un SIG es que los elementos individuales que clasificamos —las celdas de las capas—, se presentan en números muy elevados, del orden de millones. Manejar una estructura de este tipo correspondiente a tal cantidad de elementos es impracticable, por lo que directamente no puede utilizarse. Es posible aplicarla, sin embargo, sobre una clasificación ya previa que reduzca el número de elementos.

Así, dadas una serie de clases, estas a su vez pueden estudiarse mediante un proceso de clustering jerárquico para disponer de información acerca de cuáles de ellas son similares y pueden unirse para simplificar la clasificación. La combinación de ambos tipos de metodologías es una práctica que permite sacar más partido a los datos de partida, analizándolos en varias etapas.

Incorporación del criterio espacial

Hasta este punto hemos clasificado cada elemento en función únicamente de sus propios valores. Al igual que sucede en todos los casos del análisis espacial, los distintos valores con los que trabajan tienen una referencia geográfica y existe además interacción con los valores circundantes. Cada celda de las capas ráster que clasificamos se encuentra rodeada de otras celdas, y la información de estas celdas puede ser valiosa para su clasificación debido a dicha interacción.

La información que puede utilizarse puede ser tanto la correspondiente a los datos de partida (es decir, las valores de las variables estudiadas en dichas celdas circundantes) como la resultante de la propia clasificación, ya que las clases resultantes también se presentan en un contexto espacial.

Si suponemos el sencillo caso comentado anteriormente de clasificar un área de estudio en las categorías «bosque», «cultivo» y «carretera», una celda de carretera rodeada por completo de celdas de bosque no parece lógico. Este hecho puede utilizarse como ayuda a la clasificación. Con un razonamiento similar, aquellos métodos con los que es posible que existan elementos sin clasificar pueden tomar esta información contextual como apoyo. Una celda sin clasificar rodeada por celdas de bosque, lo más probable es que también ella pertenezca a esta tipología, a pesar de que a partir de sus valores el método de clasificación no haya sido capaz de establecer dicho resultado.

La incorporación de esta relación entre celdas vecinas puede llevarse a cabo a través de la utilización de filtros sobre la capa resultante. Un filtro de mayoría es una opción adecuada para homogeneizar la capa resultante y eliminar celdas aisladas cuya clase asignada no esté en consonancia con las de su alrededor.

La relación espacial entre las celdas que se clasifican puede incorporarse también antes de efectuar la clasificación, utilizando no solo la información puntual de las celdas sino también la información textural . Por «textura» entendemos la caracterización de las celdas en función de su entorno, lo cual, como puede intuirse, implica la utilización de funciones focales del álgebra de mapas. De modo similar al filtro de mayoría antes mencionado (también una función de tipo focal), la aplicación de toda la serie de filtros que vimos en el capítulo dedicado al procesado de imágenes da lugar a nuevas imágenes que pueden incorporarse al proceso de clasificación.

Para el caso de capas genéricas, no necesariamente imágenes, pueden emplearse de igual modo las distintas funciones focales tales como la media, el rango, o el valor máximo de la ventana de análisis, a seleccionar en función del significado de la variable sobre la que se aplican.

Otra forma de incorporar la relación espacial entre las celdas es la utilizada en los denominados métodos basados en objetos . Según estos métodos, no se clasifican las capas clasificando cada una de sus celdas, sino bloques de estas con características comunes. Estos bloques son los objetos , que en la fase inicial del método se estructuran de forma jerárquica a partir de esa estructura y se clasifican posteriormente.

La creación de dichos objetos a partir de las capas implica un proceso de segmentación de estas, y es ahí donde se incorpora el criterio espacial, ya que se utilizan, además de estadísticos básicos, la forma, el tamaño o los distintos descriptores de la textura de las imágenes.

Más información sobre métodos de clasificación basados en objetos dentro de un ámbito SIG puede encontrarse por ejemplo en [ Roth2003Archives ] o en [ Castilla2003PhD ], este último con un tratamiento en detalle de los métodos de clasificación, así como de los de segmentación necesarios para su empleo.

Clasificación débil ( soft classification )

En contraste con los métodos de clasificación anteriores, en particular los de clasificación supervisada, que pueden englobarse dentro de los denominados métodos de clasificación fuerte , encontramos otra filosofía distinta en los conocidos como métodos de clasificación débil . En estos, el método de clasificación no ofrece como resultado una nueva capa cuyas celdas contienen la clase a la que pertenecen, sino que la elección de dicha clase recae sobre el operador en base a los resultados que el método de clasificación produce.

Estos resultados son de forma general una serie de capas —tantas como clases a las que asignar las distintas celdas existan—, en los cuales el valor de cada celda indica la probabilidad de que dicha celda pertenezca a la clase en cuestión. De este modo, los clasificadores de tipo suave representan una etapa intermedia dentro del proceso de clasificación, ya que recogen los valores que se calculan a lo largo de este, pero no dan un veredicto posterior en base a ellos.

Si se toma el conjunto de las capas y se aplica un operador local de tipo «capa de máximo valor», el resultado que se obtendrá será una única capa, que coincidirá con la que se obtiene directamente al aplicar el método de clasificación supervisada de la forma habitual (es decir, como clasificación fuerte).

¿Cuál es la ventaja que se obtiene entonces al aplicar un método de clasificación débil y obtener las capas intermedias? En general, la información que estas capas intermedias contienen es más detallada, y además de poder emplearse para la obtención directa de la capa clasificada —el producto más habitual—, pueden utilizarse para dar una interpretación adicional a la pertenencia de cada celda a una u otra de las clases definidas.

Por ejemplo, resulta de interés conocer no solo cuál es la clase con mayor probabilidad sino también aquella que se sitúa inmediatamente después. Si clasificamos un píxel como «bosque caducifolio» y la segunda clase más probable es «bosque de coníferas», esa asignación de clase no tiene el mismo significado que si dicha segunda clase más probable es «barbecho».

De igual modo, la diferencia entre la probabilidad de la primera y la segunda clase nos dan una idea de la fiabilidad con que podemos afirmar que una celda dada pertenece a la clase a la que es asignada. En relación con este hecho se define el concepto de incertidumbre de clasificación , el cual para una celda dada se expresa mediante la siguiente fórmula:

\begin{equation} IC = 1- \frac{\mathrm{max} - \frac{S}{n}}{1-\frac{1}{n}} \end{equation}

donde $max$ es la probabilidad máxima de entre todas las correspondientes a las distintas clases, $S$ la suma de todas las probabilidades para la celda en cuestión, y $n$ el numero de clases posibles.

Otra de las posibilidades que los métodos de clasificación suave aportan es la clasificación a nivel de detalle mayor que el propio píxel. El hecho de disponer de varios valores para cada píxel hace que se pueda inferir información acerca de la variabilidad que se da en el mismo, y pueden así definirse píxeles mixtos, es decir, que no pertenecen puramente a una clase, sino a varias.

Por ejemplo, si en un píxel dado tiene una probabilidad de 0,69 de pertenecer a la clase «bosque de coníferas» y un 0,31 de pertenecer a la clase «bosque caducifolio», puede entenderse que la masa boscosa del píxel esta formada por ambos tipos de especies, caducifolias y coniferas, en las proporciones que indican sus probabilidades asociadas.

Esta interpretación viene condicionada, no obstante, al cumplimiento de ciertas condiciones tales como la pureza de las zonas de entrenamiento (que no existan píxeles mixtos en los empleados para extraer las características de cada clase), circunstancia que en muchos casos es difícil de encontrar. Aun así, los valores de probabilidad de las clases, correctamente interpretados, ofrecen mayor detalle que un simple valor de clase.

Validación

Del mismo modo que en el capítulo Creacion_capas_raster veíamos la manera de verificar la bondad de un método de interpolación a través del uso de puntos muestrales de comprobación, a la hora de clasificar un conjunto de capas en clases podemos contrastar el resultado obtenido si disponemos de zonas conocidas de antemano. Estas zonas se definen del mismo modo que las zonas de entrenamiento, pero no se utilizan para la clasificación, del mismo modo que no empleábamos los puntos de comprobación en el proceso de interpolación. Comparando los valores de clase de estas zonas de comprobación y los obtenidos mediante la clasificación podemos obtener índices de concordancia que permitan juzgar la corrección de dicha clasificación.

Los métodos que se emplean para esta tarea no son exclusivos de la clasificación de imágenes, sino que se adaptan de forma genérica a cualquier proceso que requiera la comparación de dos capas con información categórica. Al validar una clasificación, comparamos la capa resultante de dicha clasificación con una segunda con valores correctos de clases.

Otra circunstancia habitual en la que suelen utilizarse estos métodos es para comprobar la variación de clases a lo largo de un periodo. Comparando mediante estas técnicas la capa correspondiente al inicio del periodo con la del final de este, puede describirse y cuantificarse el cambio sufrido por las clases. Este planteamiento es muy útil, por ejemplo, para analizar el cambio en los usos de suelo de una zona.

El parámetro más sencillo que describe la similitud entre dos capas categóricas es el porcentaje de celdas coincidentes:

\begin{equation} c = \frac{N_c}{N} \end{equation}

donde $c$ es la concordancia global entre las dos capas, $N_c$ el número de celdas que presentan el mismo valor en ambas capas y $N$ el número total de celdas existentes.

Autores como [ Anderson1976USGS ] recomiendan al menos valores de 0.85 para considerar que la capa clasificada es operativa a efectos prácticos.

Este parámetro es sumamente sencillo y no refleja la naturaleza de la modificación que se produce entre las capas (o en el caso de utilizarse para validar una clasificación, la naturaleza del error cometido), por lo que pueden encontrarse alternativas más elaboradas.

Uno de los elementos habituales en estudio de las diferencias entre dos capas categóricas es la denominada matriz de confusión o matriz de contingencias , que ya mencionamos en el capítulo dedicado a la calidad de los datos espaciales. Se trata de una matriz de dimensiones $n\times n$, siendo $n$ el número de clases diferentes que existen en el conjunto de las capas. El elemento $(i,j)$ de la matriz representa el número de celdas que pertenecen a la clase $i$ en la primera capa y sin embargo están dentro de la clase $j$ en la segunda.

La tabla \ref{Tabla:Matriz_contingencias} muestra una posible matriz de contingencias para el caso de dos capas con un total de 4 clases.

Clase	A	B	C	D
A	20135	15	20	0
B	22	18756	133	512
C	19	70	30452	345
D	3	457	272	7018

$$\label{Tabla:Matriz_contingencias}$$

Con los valores anteriores puede comprobarse entre qué clases se dan los mayores cambios (los mayores errores de clasificación) o cuáles son las que presentan una clasificación más robusta. Por ejemplo, las clases D y B parecen ser difíciles de clasificar, ya que el numero de celdas de la primera asignados a la segunda es elevado, y también al contrario. Por el contrario, la clase A parece no presentar problemas, ya que tanto su fila como su columna correspondiente presentan ambas valores bajos fuera de la celda $(1,1)$, que es la que representa las celdas correctamente clasificados.

Este último resultado de robustez de clasificación por clases puede calcularse con la proporción de celdas correctamente clasificadas respecto a todas las clasificadas en dicha clase. La suma total de la fila k-esima dividida entre el valor de la celda $(k,k)$ representa la anterior proporción. Es decir,

\begin{equation} r = \frac{\sum_{i=1}^{n}{x_ik}}{x_{kk}} \end{equation}

Si esta misma expresión se calcula por columnas, se obtiene la proporción de celdas que, aun perteneciendo a dicha clase, han sido adjudicadas a otra distinta. Es decir,

\begin{equation} r = \frac{\sum_{i=1}^{n}{x_ki}}{x_{kk}} \end{equation}

Además de estas sencillas proporciones, existen índices más complejos que pueden también calcularse a partir de los valores de la matriz de contingencias. El más habitual es el denominado Índice Kappa de concordancia, cuya expresión es

\begin{equation} K = \frac{P_0-P_e}{1-P_e} \end{equation}

siendo $P_0$ la proporción total de celdas que coinciden en ambas capas, es decir,

\begin{equation} P_0 = \frac{\sum_{i=1}^n{x_{ii}}}{\sum_{i=1}^n\sum_{j=1}^n{x_{ij}}} \end{equation}

y $P_e$ calculado según la expresión

\begin{equation} P_0 = \sum_{i=1}^n{\frac{\sum_{j=1}^n{x_{ij}} \sum_{j=1}^n{x_{ki}} }{(\sum_{j=1}^n\sum_{k=1}^n{x_{jk}})^2}} \end{equation}

Por su expresión, el índice Kappa no presenta sesgo por una posible coincidencia casual de clases, ya que tiene en cuenta la posibilidad de que exista concordancia por azar.

A diferencia de la proporción de celdas correctamente clasificadas, cuyo rango de valores se sitúa entre 0 y 1, el índice Kappa puede tomar valores desde -1 a 1. El valor 1 indica una concordancia completa, mientras que el -1 define una correlación de signo negativa. Valores alrededor de 0 indican que no existe correlación entre las capas. Valores por encima de 0.75 indican en general una muy buena correlación.

Al igual que para la proporción de celdas concordantes, el índice Kappa puede calcularse no solo para la capa total, sino de forma individual para cada clase.

Es de reseñar que el uso de la matriz de confusión y parámetros calculados a partir de ella como el índice Kappa no es tampoco una herramienta completa a la hora de recoger la naturaleza del error que se comete en la clasificación. Por una parte, se recoge este error en toda la extensión de la capa, mientras que puede darse de forma más notable en determinadas áreas de esta [ Goodchild1994JVS ]. El error de clasificación no es constante a lo largo de toda la zona estudiada.

Por otra parte, la comprobación puede no ser espacialmente representativa. Si comparamos dos capas correspondientes a dos instantes distintos para ver la forma en que entre esos instantes han variado las clases presentes en la zona de estudio, utilizamos toda las celdas de la capa para la verificación. Sin embargo, al comprobar la clasificación de una serie de capas, se compara el resultado tan solo en unas zonas determinadas conocidas (si estas zonas conocidas que no empleamos en la clasificación cubrieran toda la extensión, no sería necesaria la clasificación). El hecho de utilizar zonas que conforman habitualmente bloques y son relativamente homogéneas introduce un sesgo que en general hace que la matriz de confusión presente una mayor precisión que la que realmente existe [ Plourde2003PHE ].

Además de las consideraciones espaciales anteriores, también deben considerarse las relaciones en el espacio de atributos. Es decir, las relaciones entre las clases. La matriz de confusión no considera estas relaciones, que sin embargo deberían tenerse en cuenta para evaluar el verdadero significado de sus valores.

Supongamos que se clasifica un área de estudio en tres clases de usos de suelo como «bosque caducifolio», «bosque de coníferas» y «lago». Si en un emplazamiento encontramos un bosque caducifolio, es un error tanto clasificarlo como bosque de coníferas como asignarlo a la clase de lago, pero no cabe duda que esta segunda posibilidad supone un mayor error. Al no existir ponderación de las celdas de la matriz de confusión a la hora de calcular índices de concordancia, este hecho no se tiene en cuenta.

El hecho de que los bosques de coníferas y caducifolios sean clases similares entre sí y los lagos sean una clase bien distinta, hace aparecer un nuevo elemento descriptor de las circunstancias que se dan en la clasificación: la separabilidad . El concepto es sencillo: resulta más fácil distinguir un bosque de coníferas de un lago, que hacerlo de un bosque caducifolio. Esta mayor facilidad o dificultad también se traduce a los algoritmos de clasificación como los que hemos visto.

La separabilidad mide la posibilidad de discriminar de forma efectiva entre clases distintas, y puede estudiarse mediante métodos visuales o bien numéricamente. El empleo de diagramas [ Jensen1996Prentice ] o la utilización de parámetros como la distancia de Jeffries--Matushita o el índice de Fisher son algunas de las alternativas para evaluar la separabilidad.

Puede encontrarse más al respecto en [ Mather1990PRS ], [ Mather1999Wiley ] o [ Thomas1987Adam ]

Regresión espacial

Ya hemos tratado anteriormente algunos conceptos estadísticos, y hemos comentado cómo la aplicación de estos dentro de un contexto espacial puede no ser del todo correcta, al asumirse ciertas condiciones que no se han de cumplir necesariamente (véanse los capítulos Estadistica_espacial y Analisis_espacial )

Uno de los análisis estadísticos con una presencia muy habitual en el ámbito SIG es el uso de regresiones, sean estas simples o múltiples. Como vimos en Ajuste_de_polinomios , a partir de los valores de una serie de predictores en un punto se puede estimar el valor en dicho punto de otra variable dada, conociendo la relación que existe entre ellas, de la forma

\begin{equation} \label{Eq:Regresion_multiple} \widehat{z} = h_0 + h_1x_1 + …, h_nx_n + e \end{equation}

siendo $h_1, h_2 … h_n$ los predictores y $z$ la variable estimada. El parámetro $e$ representa el error, que se supone distribuido normalmente.

Llevando a cabo este tipo de regresión, se asume que las observaciones son independientes entre sí, algo que no es en absoluto cierto en gran parte de los casos en los que se emplean datos geográficos.

El modelo anterior supone igualmente que a lo largo de la zona estudiada no existen variaciones de los parámetros estimados, es decir, que estos son constantes con independencia de la localización. Esta segunda suposición tampoco ha de ser necesariamente correcta, ya que en el contexto espacial en el que se disponen las observaciones sobre las que se basa la regresión, pueden existir variaciones locales de los parámetros de ajuste.

De existir esta variación, debe entenderse como parte del error. Adaptar las formulaciones habituales para el cálculo de regresiones al ámbito espacial en el que trabajamos requiere superar de uno u otro modo las anteriores circunstancias, y buscar la manera en que la variación no forme parte del residuo. De las soluciones existentes, una de ellas, construida sobre las anteriores ideas, es la conocida como Geographically Weighted Regression (GWR)[ Fotheringam2002Wiley ]. En este modelo de regresión, la ecuación \ref{Eq:Regresion_multiple} se expresa de modo más genérico como

\begin{eqnarray} \label{Eq:GWR} \widehat{z}(u,v) &=& h_0(u,v) + h_1(u,v)x_1 \nonumber\\&&+ …, h_n(u,v)x_n\nonumber \\&& + e(u,v) \end{eqnarray}

En este caso, también los parámetros estimados dependen la localización, que viene expresada a través de las coordenadas $u$ y $v$

La estimación de estos parámetros exige también adaptar el método de Mínimos Cuadrados Ordinarios, utilizado habitualmente para la estimar los de la ecuación \ref{Eq:Regresion_multiple}. Los parámetros para un modelo de regresión lineal se obtienen según la expresión matricial

\begin{equation} h = (X^TX)^{-1}X^TY \end{equation}

Añadiendo una ponderación que dependa a su vez de la localización, tenemos la siguiente expresión, que permite calcular los parámetros de la ecuación \ref{Eq:GWR}.

\begin{equation} h = (X^TW(u,v)X)^{-1}X^TW(u,v)Y \end{equation}

siendo $W$ los pesos a utilizar.

Estos pesos se toman de tal forma que las observaciones situadas más cerca del punto donde desean estimarse los parámetros tienen mayor influencia. Este tipo de formulaciones de ponderación en función de la distancia ya las hemos visto en el capítulo Creacion_capas_raster , tanto para la interpolación como para el cálculo de densidades. En el caso del GWR, una función habitual es la siguiente:

\begin{equation} w_i(u,v)= e^{\left({\frac{-d}{h}}\right)^2} \end{equation}

donde $d$ es la distancia entre las coordenadas de la observación y $(u,v)$, y $h$ es la anchura . Este parámetro es el equivalente al radio máximo de influencia que veíamos para el cálculo de densidad empleando un núcleo gaussiano.

Evaluación multicriterio y combinación de capas

La combinación de capas es una operación muy habitual. Diferentes variables, cada una de ellas recogida en una capa, se combinan para obtener algún tipo de resultado en base a la información que representan. Dentro de un SIG, conocemos ya operaciones de combinación de capas tanto en formato ráster (mediante el álgebra de mapas y sus funciones focales) como en formato vectorial (mediante operaciones de solape). Es, no obstante, con las primeras con las que podemos plantear expresiones complejas que incorporen esas variables, tal como, por ejemplo, la Ecuación Universal de Pérdidas de Suelo (USLE) que vimos en su momento en el apartado Introduccion_algebra_de_mapas .

En algunos casos, como el de la USLE, partimos de una formula definida en la que no cabe modificación alguna (este es el caso habitual con fórmulas empíricas o de base física). La formula contiene una serie de variables y cada una de estas se encuentra recogida en una capa. Basta aplicar dicha fórmula mediante una operación local del álgebra de mapas, y el resultado es una capa con la variable resultante de dicha fórmula.

En otras ocasiones, la fórmula no viene definida de antemano, sino que disponemos de una serie de variables que tienen influencia sobre un determinado fenómeno y necesitamos combinarlas para obtener una nueva variable que nos aporte información sobre ese fenómeno. El objetivo es agregar las variables de las que disponemos, como factores implicados en el proceso que analizamos.

Esta última situación es muy habitual dentro de un SIG, en los denominados procesos de evaluación multicriterio . En estos, se dispone de una serie de parámetros que afectan a un determinado fenómeno, y se pretende evaluar la medida en que afectan y condicionan al mismo, para de este modo estudiarlo y, en la mayoría de los casos, tomar decisiones en función de los resultados obtenidos. Cada una de las variables que influyen se recoge de forma habitual como una variable en una capa independiente, y se debe en primer lugar juzgar cómo los valores de cada variable afectan al fenómeno, y después combinar todas esas afecciones en una única variable que sea la que ayude en la toma de decisiones.

La evaluación multicriterio es la base de, por ejemplo, el análisis de idoneidad, un análisis muy frecuente en el ámbito SIG, y en el cual se pretende localizar dentro de una zona de estudio los mejores emplazamientos para una determinada actividad. Cada uno de los factores que influyen en el desarrollo de dicha actividad son valorados de forma independiente, y después conjugados mediante una expresión matemática.

Estas formulaciones incorporan elementos probabilísticos diversos, y existe un gran número de metodologías para formular los modelos que nos llevan a evaluar la idoneidad de cada localización. Será en estos elementos en los que nos centremos en este apartado del capítulo, con objeto de extender la potencialidad del álgebra de mapas para la realización de este tipo de operaciones. Aunque una aplicación fundamental de todos ellos es la evaluación multicriterio (y por ello están incorporados en este apartado), tienen utilidad también en otro tipo de modelos, tales como, por ejemplo, modelos de predicción de cambios en el uso de suelo, también frecuentes en el campo de los SIG.

En líneas generales, presentaremos formulaciones que nos permitan combinar las variables de forma más elaborada, para poder crear modelos geográficos de cualquier índole (como por ejemplo los modelos de idoneidad mencionados) y más precisos que los que pueden obtenerse con los elementos que hemos visto hasta el momento.

Dos son los apartados en los que ampliaremos nuestros conocimientos sobre la elaboración de modelos como los anteriores:

• La creación y preparación de las capas que reflejan los distintos criterios a aplicar
• La forma de combinar esos criterios en una expresión matemática.

Creación de capas a combinar

A la hora de plantear un modelo con diferentes variables y criterios, necesitamos expresar de forma numérica el valor de esos criterios que posteriormente agregaremos. En el caso de un modelo de idoneidad, por ejemplo, necesitamos crear una capa que nos diga si la actividad puede o no llevarse a cabo en función de cada criterio.

Como vimos en el capitulo dedicado al álgebra de mapas, además de las operaciones aritméticas podemos aplicar de igual modo operaciones lógicas a la hora de combinar varias capas. Este tipo de conceptos lógicos también estaban implícitos en las operaciones de solape entre capas vectoriales, según también vimos en su momento. Nos servían, por ejemplo, para eliminar de una capa todas las zonas a menos distancia de un cauce que el Dominio Publico Hidráulico (DPH) de este, de tal modo que restringíamos las zonas donde podíamos establecer una edificación a aquellos puntos fuera de dicho DPH. Esa distancia la calculábamos realizando un área de influencia, proceso que podríamos de igual modo llevar a cabo con capas ráster.

Ese era un modelo de idoneidad muy sencillo, con un único criterio: la distancia al cauce. Esta distancia daba lugar a dos posibles estados: o bien un punto está dentro del DPH (no se puede construir en él), o bien está fuera (se puede construir en él). Las operaciones lógicas nos sirven para expresar esto, y mediante ellas podemos desarrollar nuestro modelo.

No obstante, y sin necesidad de añadir más criterios que compliquen el modelo (es decir, sin necesidad de que la evaluación sea multicriterio, sino por el momento monocriterio), podemos encontrar situaciones en las que la lógica booleana no refleja con suficiente precisión un criterio dado. Sigamos utilizando el criterio de distancia, pero en este caso supongamos el siguiente caso: buscamos un lugar donde emplazar una fabrica y conocemos el emplazamiento del principal núcleo urbano. En este caso debemos igualmente mantenernos alejados de la ciudad para evitar las afecciones que la fábrica puede causar sobre ella. Por otra parte, sin embargo, no interesa situarla a demasiada distancia, ya que entonces será muy costoso acceder a los servicios de las ciudades.

Igual que en el caso anterior, podemos definir una distancia fija por debajo de la cual no debemos construir, y añadir además una distancia límite por encima de la cual tampoco resulta rentable económicamente hacerlo. De esta forma, planteamos nuestro sencillo modelo aunque, como veremos, es fácilmente mejorable.

Supongamos que establecemos esa distancia mínima en 4000 metros y la máxima en 15000. Un punto situado a 4001 metros es perfectamente viable, mientras que uno a 3999 no lo es. De igual modo, ese punto situado a 3999 metros es igual de inviable que uno situado a tan solo 2 metros, y puntos a 4001 metros y 14999 metros son igualmente viables, sin que exista distinción entre ambos. Estos casos no parecen muy lógicos a primera vista, y esto es debido a que, en realidad, no existen solo dos posibles clases como estamos planteando en el modelo. Un punto puede ser no solo adecuado o no adecuado , sino que existe toda una gama de posibles categorías tales como muy adecuado , poco adecuado , completamente inviable o adecuado pero casi inviable .

En el caso del DPH, este criterio plantea una restricción . A efectos de este criterio no importa el valor de la distancia, sino tan solo si es mayor o menor que el umbral, que es lo que, en base a la legalidad vigente, nos permitirá construir o no. En el ejemplo que ahora proponemos, sin embargo, no tenemos una restricción, sino una variable que condiciona, y este condicionamiento puede darse a diferentes niveles, presentando más de dos alternativas posibles.

Un caso similar lo podemos encontrar si tenemos un MDE y conocemos la altitud a la que aparece una determinada especie de planta. Esta altitud vendrá definida por un limite inferior y uno superior, pero ello no quiere decir, lógicamente, que un metro por debajo de la cota inferior o un metro por encima de la superior sea imposible encontrar dicha especie, ni que dentro de ese rango óptimo sea igual de probable encontrarla con independencia de si nos situamos cerca o no de los límites establecidos. Para reflejar este hecho necesitamos, igual que en el caso anterior, poder expresar que no solo existen zonas óptimas o inviables para una especie, sino que pueden existir otras zonas adecuadas o zonas poco adecuadas pero no completamente inviables .

Como vemos, el lenguaje natural nos ofrece una variedad de posibilidades que la lógica booleana, con su binomio verdadero/falso no nos ofrece. El objetivo es, pues, trasladar toda esa gama de posibilidades a una forma compatible con el manejo de capas dentro de un SIG y con la realización de operaciones entre conjuntos, del mismo modo en que lo hacíamos al aplicar el álgebra booleana. La solución a esto es la denominada lógica difusa .

La lógica difusa pretende acomodar las ideas anteriores al ámbito matemático, y que las operaciones lógicas no solo se basen en sí (verdadero) y no (falso), sino también en opciones intermedias ( quizás ) Esto nos va a permitir desarrollar modelos más precisos, y nos dará la posibilidad de aplicar las herramientas algebraicas que ya conocemos, más potentes en este sentido que las operaciones lógicas. Además, podremos aplicar los elementos que veremos en la siguiente sección, para combinar las capas que gracias a la lógica difusa obtendremos.

Básicamente, la idea es que, si antes expresábamos esa naturaleza verdadera o falsa de un elemento con total probabilidad (cuando era verdadero existía una probabilidad del 100% de que la planta se diera a esa altitud, y cuando era falso esa probabilidad era del 0%), ahora queremos que los valores de probabilidad no sean un conjunto finito de dos elementos, sino que puedan situarse en todo el rango de valores posibles.

La idea de esa variable «difusa» que queremos obtener es similar a la de probabilidad, y ambas se expresan como un valor entre 0 y 1, aunque conceptualmente presenten diferencias. La probabilidad nos expresa en qué grado resulta factible que se produzca un fenómeno (por ejemplo, qué probabilidad hay de que aparezca una especie de planta en función de la altitud), mientras que la variable difusa nos expresa una incertidumbre acerca de la pertenencia de un elemento a una clase (por ejemplo, en qué medida un punto, en función de su distancia a una ciudad, puede incluirse dentro de los puntos viables para establecer una fábrica). Este tipo de variables resultan, por tanto, de utilidad siempre que las clases con las que trabajamos no tengan una frontera bien definida, sino que exista una transición continua entre ellas.

Este análisis resulta similar en cierta medida a lo que veíamos en el apartado dedicado a los clasificadores suaves, donde teníamos distintas capas que nos indicaban la pertenencia de un elemento a cada una de las clases definidas. La clasificación suave nos muestra los pasos intermedios de un proceso completo, el de clasificación, en el cual a partir de las variables de partida, se obtiene una capa resultante.

Como indica [ Maguire2005ESRI ], existen dos formas de plantear estos modelos: por un lado, tratar las variables por separado y después agregarlas, o bien establecer un planteamiento holístico que trate todas estas variables como un conjunto. La clasificación está en este último grupo. Las operaciones que vemos dentro de este apartado se encuentran, sin embargo, dentro del primero.

Un elemento clave en la lógica difusa son las funciones que nos permiten calcular los valores de la variables difusa (es decir, aplicar el criterio concreto sobre cada variable). Puesto que el valor de esta nos indica la certidumbre con la que podemos afirmar que un elemento es miembro de una clase dada, las anteriores funciones se conocen como funciones de miembro . A partir de un valor dado asignan uno nuevo entre 0 (se sabe con certeza que el elemento no pertenece a la clase) y 1 (se sabe con certeza que sí pertenece a la clase).

Por ejemplo, para el supuesto de utilizar la distancia a una ciudad como variable base, una posible función de miembro es la mostrada en la figura \ref{Fig:Funcion_de_miembro}.

. $$\label{Fig:Funcion_de_miembro}$$

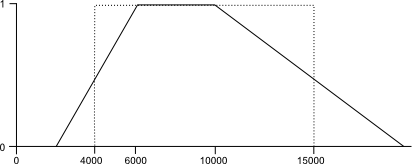
Para definir esta función de miembro, se han establecido, además de los valores límite, un rango de valores óptimos (entre 6000 y 10000 metros de distancia), que son los que delimitan las zonas idóneas para situar nuestra fábrica. En este rango, se tiene un valor 1. Desde los valores óptimos, los valores descienden, haciéndolo de tal modo que toman un valor igual a 0,5 en el punto en el que situábamos los valores límite. Esto es lógico si pensamos que hay que definir un punto umbral a partir del cual considerar si el elemento está dentro o fuera de la clase (para así tener la clasificación dicotómica de verdadero y falso), y ese punto resulta natural establecerlo en la mitad del intervalo.

Junto con la gráfica de la función de miembro anterior, se muestra la forma que tendría una función de miembro que se comportase igual que si operáramos con los elementos del álgebra booleana, restringiendo los valores posibles a dos: verdadero y falso . Esta función presenta un salto brusco del 0 al 1, de tal modo que no es posible asignar ninguno de los valores intermedios. Para cualquier valor dado, el nuevo valor que se obtiene al aplicar esta función es, o bien 0, o bien 1. El salto de la función se produce exactamente en los valores límite, justamente donde la verdadera función de miembro toma el valor 0,5.

La diferencia entre los resultados que se obtienen al aplicar una función de miembro como la anterior y aplicando una mera clasificación en dos clases de distancia pueden apreciarse en las capas de la figura \ref{Fig:Capas_logica_difusa}. Junto con una capa de distancia a un punto dado, se muestran las resultantes de, en base a dicha capa, aplicar un criterio en forma de restricción con dos clases posible (zonas dentro del intervalo óptimo vs. zonas fuera del intervalo) o bien creando una variable que refleje la certidumbre de pertenencia a cada una de las clases anteriores.

. $$\label{Fig:Capas_logica_difusa}$$

La función de miembro puede ser cualquier función, y no necesariamente similar a la que se muestra en la figura \ref{Fig:Funcion_de_miembro}. Basta con que cumpla las siguiente condiciones:

• Estar acotada entre 0 y 1
• Asignar valor 1 a los elementos que indudablemente pertenecen al conjunto o clase
• Presentar un descenso «suave» desde los elementos con valor 1 hasta los restantes.

Es habitual, no obstante, encontrarnos con situaciones como las anteriores, en las que tengamos dos rangos, uno para el óptimo dentro del cual tendremos valor 1 (sea este rango acotado por los valores $b$ y $c$, $b < c$), y otro más amplio que abarca todos los valores distintos de 0 (entre los valores $a$ y $d$, $a < d$). En esta situación, lo único necesario es definir las transiciones desde el óptimo hasta los límites exteriores, es decir, los descensos suaves anteriormente citados.

En el ejemplo de la figura esta transición es lineal, y la función de miembro se puede definir de la siguiente manera:

\begin{eqnarray} f(x) = \left\{ \begin{array}{ll} 0 & \textrm{si $x < a$}\\ \frac{x-a}{b-a} & \textrm{si $a \leq x \leq b$}\\ 1 & \textrm{si $b < x < c$}\\ \frac{d-x}{d-c} & \textrm{si $c \leq x \leq d$}\\ 0 & \textrm{si $x > d$} \end{array} \right. \end{eqnarray}

Pueden elegirse cualesquiera valores para los parámetros $a, b, c$ y $d$, obteniéndose toda una familia de curvas distintas. Por ejemplo, el intervalo óptimo puede reducirse a un único punto ($b=c$), en cuyo caso tendríamos una función triangular.

Otra solución habitual es emplear una función sigmoidal para las transiciones, quedando la definición global de la función de miembro como sigue:

\begin{eqnarray} f(x) = \left\{ \begin{array}{ll} 0 & \textrm{si $x < a$}\\ \frac{1}{2} \left(1 + \cos \left(\pi \frac{x-a}{b-a}\right)\right) & \textrm{si $a \leq x \leq b$}\\ 1 & \textrm{si $b < x < c$}\\ \frac{1}{2} \left(1 + \cos \left(\pi \frac{d-x}{d-c}\right)\right) & \textrm{si $c \leq x \leq d$}\\ 0 & \textrm{si $x > d$} \end{array} \right.\nonumber \end{eqnarray}

Una función de distribución de probabilidad gaussiana (esto es, una campana de Gauss), también puede utilizarse como función de miembro. En este caso, el óptimo sería el punto que coincide con la media de dicha distribución.

Métodos de combinación de capas

A la hora de plantear un modelo, utilizaremos habitualmente no una única capa como en los ejemplos anteriores, sino un conjunto de ellas, pues serán con seguridad varios los factores que influyen en el fenómeno que estudiamos. Si pretendemos buscar el emplazamiento de una fábrica, la distancia a la ciudad más próxima condiciona la idoneidad de cada localización, pero también lo harán el tipo de suelo, el uso de suelo, la pendiente, y otra serie de factores.

De igual modo, la probabilidad de que una especie aparezca en un determinado punto depende de la altitud, pero también de la insolación o las características del suelo, entre otros factores. Cada uno de ellos se pueden tratar por separado, y obtenerse capas como las que hemos obtenido en el apartado anterior, con valores entre 0 y 1, que indiquen un valor de probabilidad o bien la pertenencia a un conjunto difuso. Con todas estas capas es con las que debemos plantear el modelo, agregando la información que nos suministran en una nueva variable.

Las operaciones algebraicas más sencillas nos dan una primera herramienta para esa agregación. Estadísticos como la media aritmética, la media armónica, o los valores máximo o mínimos del conjunto pueden servir para combinar en un único valor los valores de los distintos criterios [ Ayyub2001CRC ].

La mera suma de los distintos valores es empleada también con frecuencia. Si los valores representan probabilidades, esta suma corresponde al operador O. Si en lugar de la suma empleamos el producto, esto es equivalente a la operación Y, es decir, la intersección de los conjuntos (estas operaciones tienen el mismo significado si las aplicamos sobre elementos verdadero/falso codificados con valores 0/1, es decir, si la combinación es en esencia booleana).

Una opción más elaborada es una media ponderada de los distintos factores, de la forma

\begin{equation} \label{Eq:Media_ponderada} y = \frac{\sum_{i=n}{N}a_ix_i}{\sum_{i=n}{N}a_i} \end{equation}

Esta es una solución habitual en la evaluación multicriterio [ Maguire2005ESRI ].

Además de estos métodos, existen otros que, según las circunstancias, pueden resultar más adecuados para una correcta combinación de los factores considerados. Entre ellos, encontramos la denominada regla de Dempster . En el caso de aplicar una media ponderada como la de la ecuación \ref{Eq:Media_ponderada}, la elección de los pesos $a_i$ no es trivial, especialmente cuando el número de factores es elevado. La metodología de Jerarquías Analíticas , que también veremos, nos ayudará a establecer dichos pesos de forma coherente con la importancia de cada factor.

Regla de Dempster

La regla de Dempster esta basada en la denominada Teoría de la Evidencia , una extensión de la teoría bayesiana de la probabilidad [ Shafer1976Princeton ].

El elemento básico para agregar las distintas evidencias dentro de esta teoría es la regla de Dempster. La característica principal de esta regla es que, al contrario que el producto de las probabilidades, no disminuye a medida que se agregan más y más factores (en el producto, por ser la probabilidad siempre menor que 1, sí sucede así). En particular, si se agregan dos valores mayores que 0,5 el resultado es mayor que ambos. Si se agregan dos valores menores que 0,5 el resultado es menor que ambos. Si uno es mayor y otro menor, el resultado es intermedio entre ambos.

Las probabilidades se denotan con la letra $m$ (de masa ) y se conocen como Asignación de Probabilidad Básica .

El lector interesado en profundizar en el tema puede encontrar en [ Shafer1976Princeton ][ Gordon1985AI ] exposiciones más detalladas al respecto. Más ejemplos de la regla de Dempster y de numerosas variantes de la misma pueden encontrarse en [ Sentz2002Sandia ].

Jerarquías Analíticas

Una suma ponderada de los distintos factores es uno de los métodos más habituales de combinar estos. Si los factores son solo dos, o incluso tres, no resulta difícil asignar los pesos a cada uno de ellos conociendo la importancia relativa que tienen. Sin embargo, cuando son más numerosos (lo cual sucede muy habitualmente), asignar pesos de forma consistente no resulta sencillo, ya que las relaciones uno a uno entre los distintos factores son demasiadas como para poder tener una visión global de ellas. Es necesario para ello recurrir a alguna metodología con cierta sistematicidad.

La más popular de estas metodologías es la de las denominadas Jerarquías Analíticas [ Saaty1977JMP ]. En esta metodología, no han de asignarse pesos directamente a todos los factores, sino tan solo hacerlo para cada una de las posibles combinaciones entre dos de dichos factores. Puesto que se reduce la ponderación de todos los factores simultáneamente a una serie de sencillas ponderaciones entre dos elementos, resulta mucho más sencillo establecer la importancia relativa de cada factor, a la par que mucho más preciso.

Los pesos de las distintas parejas de factores se colocan en una matriz de dimensiones $n\times n$, siendo $n$ el número de factores que se quieren ponderar. El valor en la posición $(i,j)$ representa la ponderación entre el factor $i$ y el factor $j$, esto es, la importancia relativa de este primero frente al segundo. En esta matriz (sea $M$), se cumple siempre que $M_{ij}=\frac{1}{M_{ji}}$, y $M_{ii} = 1$.

Existen estudios psicológicos que muestran que no se puede comparar simultáneamente más de $7\pm2$ elementos, y en base a este hecho los autores de esta metodología recomiendan utilizar valores entre 1 y 9, según lo mostrado en el cuadro \ref{Tabla:AHP}.

Valor	Descripción
1	Misma importancia
3	Predominancia moderada de un factor sobre otro
5	Predominancia fuerte
7	Predominancia muy fuerte
9	Predominancia extrema
2, 4, 6, 8	Valores intermedios
Valores recíprocos	Valores para comparación inversa

$$\label{Tabla:AHP}$$

Una vez creada la matriz de comparaciones, el autovector principal de la misma contiene los distintos pesos a asignar a cada uno de los factores.

Factores y restricciones

A la hora de combinar una serie de capas, el papel que estas juegan en el modelo puede ser bien distinto en función de la variable que contengan. Por ejemplo, existiendo una limitación legal a la construcción cerca de un cauce, trabajar con una capa de distancia al cauce con las herramientas que acabamos de ver para preparar y combinar capas no aporta ninguna ventaja adicional. La distancia no es en este caso un factor cuya influencia pueda graduarse, sino una restricción que simplemente nos servirá para saber si es posible o no construir en un emplazamiento dado.

En el caso de las restricciones, las operaciones lógicas con las que trabajábamos son suficientes para excluir aquellas zonas en las cuales no va a ser viable desarrollar una actividad, con independencia del resto de variables. En el ejemplo de la distancia al cauce para establecer una edificación, no importa que el resto de factores sean apropiados y el lugar sea idóneo para edificar. Si la distancia al cauce es menor que la establecida por el Dominio Público Hidráulico, no resulta viable como emplazamiento.

Frente a aquellos parámetros que representan restricciones, existen otros que afectan a la actividad que evaluamos en el modelo, pero su influencia puede tratarse como una variable continua, tal y como hemos visto. La combinación de estos mediante operaciones lógicas no es suficiente para reflejar este hecho, y deben por ello aplicarse operaciones aritméticas o algunas de las metodologías alternativas que hemos visto.

Esta distinción entre factores y restricciones es importante para una correcta integración de todas las capas con las que vamos a trabajar, dándole a cada una el papel que le corresponde en el modelo. Se pueden tratar las capas de factores por separado y después aplicarles las restricciones, conjugando así los dos tipos de parámetros que se consideran en el modelo.

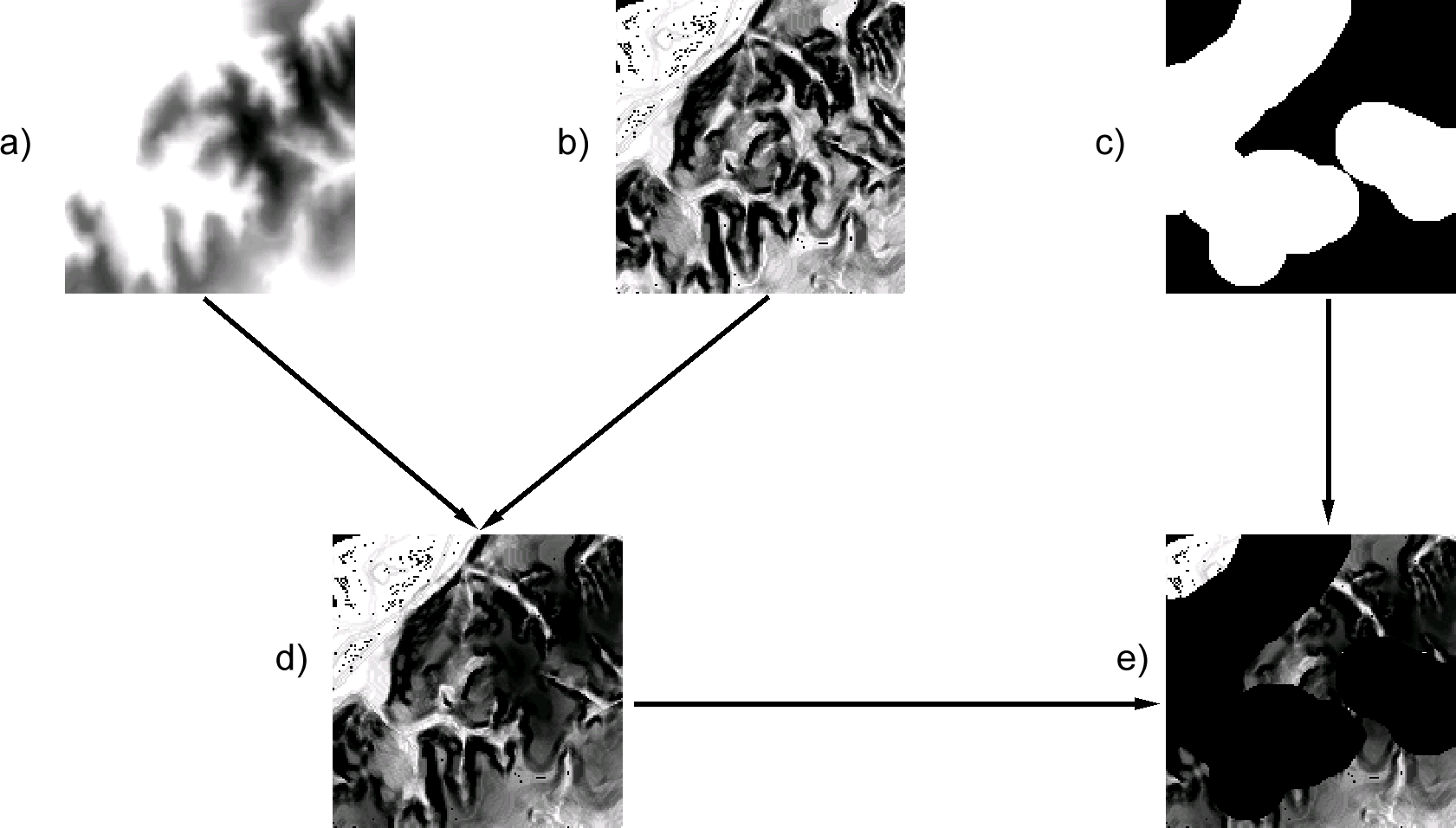
Las operaciones lógicas pueden evaluarse como operaciones aritméticas, aplicando el operador multiplicación y codificando con valores 0 y 1 los valores lógicos verdadero y falso . El ejemplo de la figura \ref{Fig:Factores_restricciones} muestra un supuesto de combinación de dos factores y una restricción en un modelo sencillo.

. $$\label{Fig:Factores_restricciones}$$

Análisis de Componentes Principales

El Análisis de Componentes Principales (ACP, también conocido como transformación de Kahunen-Loeve o de Hotelling es otra técnica estadística con gran importancia dentro de los SIG, en especial, y de modo similar a la clasificación (aunque al igual que entonces, no exclusivamente), en el trabajo con imágenes.

El ACP es una transformación que pretende disminuir la dimensionalidad de un conjunto de variables, reduciendo este a uno más pequeño de forma que se pierda la menor información posible. Se trata de «resumir» la información que esas variables contienen, pero eliminando partes redundantes como por ejemplo las derivadas de la dependencia que pueda existir entre las variables. Se busca, pues, eliminar datos sin eliminar información.

Esta trasformación es útil ya que disminuye el volumen de datos total, facilitando las operaciones de análisis e interpretación de las variables, así como su propio manejo.

En el ámbito del SIG, trabajamos con frecuencia con muchas capas, y una reducción en el número de estas facilita el planteamiento de modelos tales como los que veíamos en el apartado anterior. No solo disminuyen los cálculos a efectuar y la complejidad de las operaciones, sino que resulta más sencillo interpretar las relaciones entre variables cuando estas no se presentan en gran número (recuérdese, por ejemplo, lo que se comentó en el apartado AHP en relación a la metodología de Jerarquías Analíticas)

En el caso de imágenes con elevado número de bandas (multiespectrales e hiperespectrales), vimos en el capítulo Procesado_imagenes que la representación de estas no puede hacerse empleando todas las bandas, sino que deben prepararse composiciones con, a lo sumo, tres bandas. Reducir un conjunto de muchas bandas a uno de tres con la máxima información posible, de forma que ya pueda ser representado y analizado visualmente, resulta una metodología más adecuada que elegir tres bandas cualesquiera de ese mismo conjunto. Por su propia naturaleza, es probable además que esas bandas estén altamente correlacionadas y contengan información redundante, o al menos con cierta redundancia de cara al trabajo concreto que vayamos a llevar a cabo con la imagen en cuestión.

Por las razones anteriores, las imágenes son un tipo de dato que se presta en gran medida a la aplicación de este tipo de transformación, aunque cualquier conjunto de capas puede trasformarse de manera similar.

El planteamiento conceptual de la transformación puede resumirse de la forma siguiente. Sea un conjunto de $n$ variables. Estas definen un espacio vectorial n-dimensional, de tal forma que las características de un elemento dado (en caso de una capa ráster será una celda dada) se expresan mediante un vector de $n$ elementos de la forma ($x_1, x_2, …, x_n$). El ACP busca definir un cambio de base en ese espacio n--dimensional, de modo que los vectores de la nueva base guarden una relación directa con las direcciones de variabilidad del conjunto de datos. El primer vector de la base señala la dirección de máxima variabilidad, el segundo la segunda dirección de máxima variabilidad, y así sucesivamente. Eso quiere decir que, en esta nueva base, la mayor parte de la información se va a encontrar en la dirección del primer vector, y que esta cantidad de información va a decrecer paulatinamente según tomamos cada uno de los sucesivos vectores de la base.

Al aplicar el cambio de base a un vector ($x_1, x_2, …, x_n$), se obtiene un nuevo vector ($x'_1, x'_2, …, x'_n$), expresado en las coordenadas de la nueva base. Puesto que las primeras coordenadas de este nuevo vector se corresponden con las direcciones de máxima variabilidad, podemos tomar solo las primeras $p$ coordenadas (siendo $p < n$) y tener un vector de la forma ($x_1, x_2, …, x_p$), sabiendo que haciendo esto estamos perdiendo poca información a pesar de reducir la dimensión del vector original. Estas $p$ coordenadas son los $p$ componentes principales.

Es importante reseñar que las variables resultantes no tienen significado físico alguno aun en el caso de que las variables originales sí lo tuvieran, no pudiendo utilizarse en ese sentido del mismo modo que dichas variables originales.

Aunque resulta de interés tomar las componentes principales y descartar los vectores finales de la base, estos también pueden aportar información relevante según qué análisis se quiera realizar. La información sobre los ejes principales define aquella información que aparece en todas las variables utilizadas. La información restante es la que aparece solo en alguna de ellas. Esto puede utilizarse, por ejemplo, para estudiar los cambios producidos a lo largo del tiempo.

Si tomamos como $n$ variables un conjunto de $n$ medidas de una única variable en $n$ instantes, el análisis de componentes nos permite separar la información común a todos ellos de aquella que solo corresponde a algunos. De este modo, podemos analizar una u otra parte de la información según sean los resultados que busquemos.

En [ Fung1987PERS ] y [ Byne1980RSE ] pueden encontrarse dos ejemplos del uso de transformaciones de componentes principales en la detección de cambios de uso de suelo a partir de series de imágenes.

Para calcular la matriz del cambio de base que define la transformación, se puede partir de la matriz de covarianzas $C$ (ver ecuación \ref{Eq:Matriz_covarianzas}) o bien de la matriz de correlación $\rho$, en la cual los elementos son los coeficientes de correlación de Pearson. Es decir,

\begin{equation} \rho = \left( \begin{array}{cccc} \rho_{11} & \rho_{12} & \cdots & \rho_{1n} \\ \rho_{21} & \rho_{22} & \cdots & \rho_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{n1} & \rho_{n2} & \cdots & \rho_{nn} \\ \end{array} \right) \end{equation}

donde $\rho_{ij}$ se calcula según

\begin{equation} \rho_{ij}=\frac{\sigma_{ij}}{\sigma_{ii}\sigma_{jj}} \end{equation}

Esta ultima matriz se emplea en lugar de la de covarianzas en caso de que las unidades en que se miden las variables no guarden relación entre sí, con lo cual no es posible compararlas.

El siguiente paso una vez que se tiene la matriz es la obtención de sus autovalores y autovectores. Estos autovectores son los vectores de la nueva base, y sus autovalores asociados nos sirven para establecer el orden en que han de considerarse. Así, el mayor autovalor indica que su vector propio asociado es aquel cuya dirección es la de la máxima variabilidad, y el de mínimo valor se asocia, de modo similar, al vector en la dirección de mínima variabilidad.

Para más detalles, [ Chuvieco1996Rialp ] ofrece información detallada sobre el análisis de componentes principales y su uso en el campo de la teledetección.

Resumen

En este capítulo hemos visto algunas formulaciones estadísticas más complejas y su aplicación particular sobre datos espaciales.

La clasificación es uno de los procesos de mayor importancia y, pese a estudiarse de forma habitual aplicado sobre imágenes, es de gran utilidad sobre cualquier tipo de datos. Tomando una serie de $n$ capas ráster, la clasificación asocia cada celda a una clase dada, en función de los valores de dicha celda en esas capas.

Si en el proceso de clasificación se aporta algún tipo de información adicional sobre las características de las distintas clases, el proceso se conoce como clasificación supervisada . Si, por el contrario, se generan estas clases sin información adicional y simplemente buscando la mayor homogeneidad, el proceso se denomina clasificación no supervisada .

Otras formulaciones vistas son las relativas a la combinación de capas. A la hora de combinar varias de ellas, podemos realizar operaciones aritméticas sencillas (mediante operaciones locales del álgebra de mapas) o aplicar otra serie de formulaciones más elaboradas. Metodologías como las jerarquías analíticas permiten establecer ponderaciones más correctas cuando el número de capas a combinar es elevado y resulta difícil asignarles pesos relativos. El significado de una capa en una operación de combinación puede ser distinto en función de si representa un factor más a considerar en la ecuación, o una restricción en el modelo.

Por último, hemos visto cómo el método de análisis de componentes principales permite reducir el número de variables con los que se trabaja en un modelo, reduciendo un conjunto de $n$ capas a uno menor, tomando aquellas que explican la mayor variabilidad. Esto es de utilidad para establecer modelos de combinación entre capas, así como para reducir el volumen de datos en imágenes.