El mapa y la comunicación cartográfica

Introducción

Los mapas se han empleados desde la antigüedad para recoger la información geográfica y transmitirla. Como ya dijimos en el capítulo anterior, podemos entender un mapa como un medio de comunicación visual que constituye un lenguaje con un objetivo particular: la descripción de relaciones espaciales. Una mapa es, pues, una abstracción simbólica de algún fenómeno real, lo cual significa que presenta un cierto grado de simplificación y generalización.

El diseño, producción y uso de un mapa como forma de comunicación conforma lo que se conoce como proceso cartográfico . Más concretamente, el proceso cartográfico conlleva cuatro etapas o subprocesos, a saber:

• Recogida de los datos.
• Manipulación y generalización de los datos para diseñar y construir el mapa.
• Visualización del mapa.
• Interpretación de la información.

La labor del cartógrafo se centra en el segundo de estos puntos, mientras que el usuario del mapa lleva a cabo los dos últimos. Será en esa construcción de los mapas en lo que nos fijemos a lo largo de este capítulo, para conocer los conceptos y reglas que rigen la comunicación cartográfica a través del uso de mapas.

El lenguaje visual que estudiábamos en el capítulo Conceptos_basicos_visualizacion se convierte ahora en un lenguaje cartográfico al adaptarlo al caso particular de la creación de mapas, y estas reglas (equivalentes a la gramática y la sintaxis de un lenguaje hablado) son imprescindibles para poder crear cartografía que facilite las citadas labores del usuario posterior de esta. Este conjunto de ideas relativas a la producción de mapas dan forma a lo que conocemos como diseño cartográfico .

El diseño cartográfico implica la toma de decisiones por parte del cartógrafo. Algunas de estas decisiones pueden ser la cantidad de simplificación que debe realizarse o los símbolos que han de emplearse para plasmar la información a transmitir. Las ideas desarrolladas en los próximos apartados conforman una base de conocimientos que facilita la toma de decisiones correctas en este sentido.

El propósito del mapa

Como elemento de comunicación, un mapa tiene siempre un propósito. De la misma forma que al hablar pretendemos transmitir algo y para ello usamos el lenguaje como herramienta, en el caso de crear un mapa empleamos el lenguaje gráfico para transmitir una determinada información geográfica. También de igual modo que en el caso de la comunicación verbal, y en el de cualquier otra forma de comunicación, existe un receptor de nuestro mensaje. Es decir, un usuario (o varios) de ese mapa, que serán quienes lo interpreten y aprovechen.

Esto que parece obvio es un hecho que se ignora muchas veces a la hora de elaborar un mapa, y con ello se pierde gran parte de la capacidad del mapa como elemento de comunicación. Aplicar los conceptos de visualización correctamente, así como aquellos que veremos en este capítulo relativos a la simbolización, no garantiza que el mapa que generemos sea útil, del mismo modo que aplicar adecuadamente la gramática del chino para elaborar una frase no sirve de nada si nuestro interlocutor solo habla castellano. No será capaz de interpretar nuestro mensaje por muy correcto que este sea. Resulta incluso mejor elaborar un mensaje con errores gramaticales en castellano, ya que al hacerlo así estamos teniendo en cuenta las circunstancias en que se produce la comunicación.

Al crear un mapa nunca debemos olvidar quién y para qué va a usar ese mapa, y en función de ello elegir los elementos correctos y la forma de presentar la información más acorde con esos destinatarios y sus objetivos particulares. Sólo entonces es cuando aplicaremos los conceptos del diseño cartográfico para que el mensaje que elaboramos sea el mejor posible.

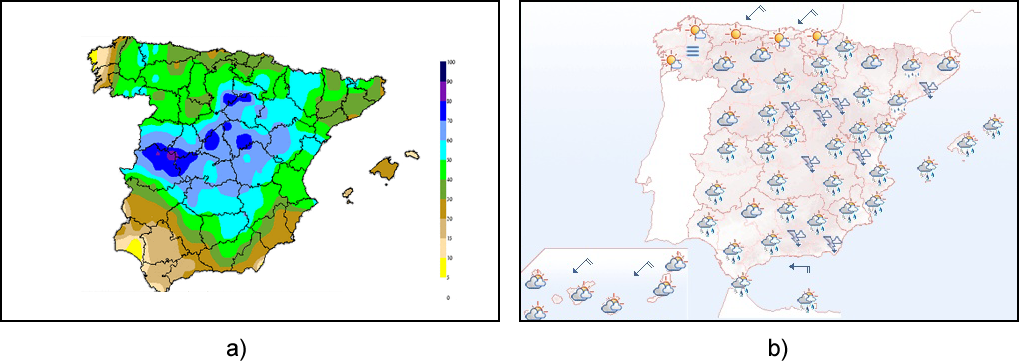
La figura \ref{Fig:PropositoMapa} muestra un ejemplo claro de lo anterior a través de dos mapas con predicciones meteorológicas, proporcionados por la Agencia Estatal de Meteorología de España. El primero es un mapa de probabilidad de precipitación, mostrada esta mediante isolíneas. El segundo es un clásico mapa del tiempo (conocido como mapa significativo ) en el que sobre el mismo territorio se sitúan símbolos indicando el tiempo previsto (soleado, chubascos, lluvias, tormentas, etc.).

Ambos mapas son correctos desde el punto de vista de la labor cartográfica y se han creado a partir de una misma información, pero la forma de mostrar esta es bien distinta. Para un uso científico, este último mapa resulta claramente insuficiente, mientras que el primero es adecuado. Sin embargo, si la audiencia es no especializada, tal como los lectores de un periódico que deseen saber si mañana podrán o no salir al campo a disfrutar de un día soleado, el segundo mapa es mucho mejor, ya que el primero, aunque también proporciona esa información e incluso lo hace con más detalle, puede resultar excesivamente complejo y difícil de entender si no se tienen ciertos conocimientos. Es decir, el usuario es en última instancia, y por encima del propio diseño cartográfico, quien hace que el mapa sea o no un elemento útil.

$$\label{Fig:PropositoMapa}$$

Entre los elementos fundamentales que se han de elegir en función del propósito del mapa se encuentran los correspondientes a la base matemática del mapa: escala y proyección. La escala condicionará el tipo de estudios que será posible llevar a cabo con el mapa, y establecerá el nivel de detalle que se desea comunicar a través de este (siempre, obviamente, dentro de los limites de la escala a la que se hayan recogido los datos). Por su parte, la proyección debe considerarse en función de sus propiedades. Como ya vimos en el apartado TiposProyecciones , toda proyección implica algún tipo de distorsión. Existen así proyecciones que mantienen las áreas, las distancias o los ángulos. Según qué trabajo se espere con el mapa, será más indicado hacer uso de una u otra de ellas, ya que no es lo mismo un mapa catastral que una carta de navegación, y la elección de una proyección inadecuada puede convertir un mapa en una herramienta inútil para la tarea que se pretende realizar.

El otro aspecto importante a considerar es la forma en que transmitimos la información a través del mapa, es decir, el tipo de mapa, como hemos visto en el ejemplo propuesto. Dentro de este capítulo estudiaremos los tipos de mapas más habituales y las características que los definen, así como la forma de crearlos correctamente.

Cartografía temática y cartografía base

Existen muchos tipos de mapas y muchas formas de clasificarlos. Una clasificación especialmente relevante es la que divide a estos en dos grupos cartográficos principales en función del tipo de información que aporten: cartografía base , también denominada fundamental o topográfica , y cartografía temática .

La cartografía base representa el tipo de mapa que originalmente era el objeto principal de la cartografía, cuando lo primordial era recoger con precisión qué había sobre la Tierra, documentando a través del documento cartográfico las características físicas de esta. Este tipo de cartografía requiere de medidas precisas y se basa fundamentalmente en el trabajo de la topografía para obtener la información necesaria que posteriormente se plasma sobre el mapa.

La cartografía base tiene carácter general, y ello explica que inicialmente fuera el único tipo de mapa de interés para el cartógrafo, ya que existía una indudable necesidad de ese tipo de información de referencia acerca del entorno físico. Una vez que se ha desarrollado una colección suficiente de mapas topográficos y se conoce bien la Tierra a través de ellos, los cartógrafos comienzan a recoger en otro tipo de mapas otras variables espaciales también susceptibles de ser representadas de ese modo. Esto tiene lugar alrededor del siglo XVIII, y aparece entonces la cartografía temática.

La cartografía temática se centra en la representación de un tema concreto (una variable espacial dada), pudiendo ser esta de cualquier índole: física, social, política, cultural, etc. Se excluyen de la lista de esos temas posibles a los puramente topográficos, que constituyen el objeto de la cartografía base.

La cartografía temática se apoya en la cartografía base, ya que esta se incluye también en los mapas temáticos para facilitar la comprensión del comportamiento espacial de la variable representada y ubicar esta en un contexto geográfico dentro del propio mapa. Un mapa temático se compone, así pues, de dos partes bien diferenciadas:

• Una capa específica con la información temática. Contiene la información principal del mapa, que representa la variable espacial sobre la que se construye este.
• Un mapa base. El mapa base provee una localización geográfica a la que se referencia la información temática. Debe contener los elementos propios de la cartografía base, aunque siempre ha de tenerse en cuenta que estos han de coexistir con los correspondientes a la parte temática. Por ello, frecuentemente es necesario incluir en este mapa base menos detalle que si se diseñara para ser un mapa independiente, limitándose a los elementos necesarios que definan un contexto geográfico básico. La labor de este mapa base no es ser utilizado como tal como si se tratara de cartografía base aislada, sino ayudar a los elementos de la componente temática a transmitir mejor la información que contienen.

  Aunque en ocasiones puede utilizarse un mapa topográfico estándar como mapa base, habitualmente este contiene demasiada información e interfiere con la capa temática, siendo más adecuado crear el mapa base a partir de elementos individuales. Algunos de los más importantes son el canevás (rejilla de coordenadas, especialmente necesaria a escalas pequeñas), la red fluvial, el relieve, la vías de comunicación, las poblaciones y los nombres geográficos. Todos ellos son buenos elementos de referencia para permitir situar en base a ellos cualquier tipo de información temática.

La mayoría de las ideas de este y el próximo capítulo se aplican fundamentalmente a la cartografía temática, siendo esta además la que con mayor frecuencia se genera mediante el uso de un SIG. Una buena parte de lo visto en relación con las variables visuales y sus propiedades tiene mayor relevancia a la hora de tratar con cartografía temática, ya que esos conceptos se aplican a la representación de variables y fenómenos de tipo cuantitativo, y es la cartografía temática la que trabaja con ellos.

En la cartografía topográfica, los elementos geométricos que representamos son en sí la información que pretendemos comunicar con el mapa, mientras que en la cartografía temática esa geometría es solo parte de la información, siendo la otra parte la que se transmite a través del uso de variables visuales como, por ejemplo, el color. De otro modo, la cartografía topográfica representa «cosas» que encontramos en el terreno (un accidente geográfico, el curso de un río, el perfil de una costa), mientras que la cartografía temática se centra más en la representación de valores y atributos. La línea que representa una carretera en un mapa existe realmente en el terreno, mientras que la que representa una curva de nivel no existe físicamente. Podemos decir también que en lugar de en el qué , la cartografía temática se centra en el cómo .

Según el tipo de información que contenga, la cartografía temática se divide en cuantitativa y cualitativa. Como veremos a continuación, el tipo de información tiene gran repercusión a la hora de generar un mapa, ya que condiciona los elementos que podemos usar para simbolizar dicha información.

Los tipos de información y su representación

$$\label{Fig:LeerVer}$$

Como vimos en el apartado ComponenteInformacionGeografica , la componente temática de la información geográfica puede ser de tipo numérico o alfanumérico, y la primera se divide en los tipos nominal, ordinal, intervalos y razones. Nominal y alfanumérico representan información cualitativa, mientras que los restantes representan información cuantitativa. Esta división tiene una enorme importancia a la hora de visualizar la información temática, ya que simbolizar esta es distinto en función de sus propias características, y el uso de un esquema erróneo dará como resultado un mapa en el que no se produce una adecuada transmisión de la información. Escoger la forma adecuada de efectuar esa simbolización garantizará que los elementos visuales comunican de la mejor forma posible toda la información a la que hacen referencia. Esto puede verse claramente en el ejemplo mostrado en la figura \ref{Fig:LeerVer}.

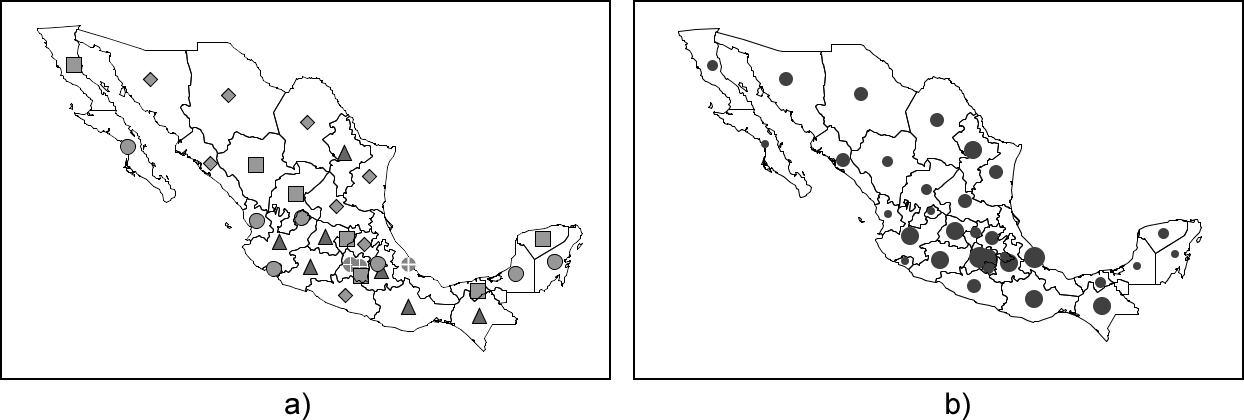
Los mapas de la figura representan en ambos casos la población de los distintos estados de México, pero en cada uno de ellos se emplea una forma distinta de simbolizar los valores de población. En el primero de ellos (caso a) se ha dividido la población en cinco clases, cada una de las cuales se identifica mediante un símbolo. Los símbolos han sido escogidos de forma arbitraria, y no existe una relación entre ellos. Por su parte, el ejemplo b) también emplea símbolos y presenta igualmente cinco clases, pero en este caso tienen todos las misma forma, y lo que varía es el tamaño. Se puede establecer una relación entre los símbolos, ya que estos pueden ordenarse en función de su tamaño.

Siendo la población una variable que también puede ordenarse, el caso b) es claramente más adecuado, ya que nos proporciona la información visual de forma más rápida e inmediata. No solo responde a la pregunta ¿qué población tiene esta provincia? , sino también a otras como ¿dónde está la provincia más poblada? En el caso a) podemos conocer también la población de una provincia y si esta es mayor que la de otra, pero necesitamos para ello acudir a la leyenda, ya que no resulta obvio que el símbolo cuadrado indique más población que el símbolo círculo. Por su parte, el uso de un único símbolo y la variable visual tamaño es mucho más intuitivo, y nos transmite esa información sin necesidad de consultar la leyenda del mapa. Este hecho está directamente relacionado con las propiedades de las variables visuales, que ya estudiamos en el capítulo Conceptos_basicos_visualizacion .

Como argumenta [ Bertin1987Pompidou ], el primer mapa es una mapa que debemos leer , mientras que el segundo es un mapa que podemos ver . Puesto que un mapa es un elemento visual, es preferible que transmita de forma visual su información, y un mapa a leer supone un desperdicio tanto de tiempo como de información misma.

$$\label{Fig:RepresentacionInfoNominal}$$

Así pues, la selección de una forma de simbolización adecuada en función de la naturaleza de la información es clave para lograr un mapa efectivo. En particular, debe emplearse una variable visual que presente la propiedad (nivel de organización) adecuado. Las propiedades asociativa y selectiva solo son de interés para información cualitativa, mientras que, por ejemplo, el tamaño es la única variable visual con la propiedad cuantitativa, y por tanto la única adecuada para representar razones.

Las siguientes son algunas ideas básicas a este respecto referidas a los distintos tipos antes citados.

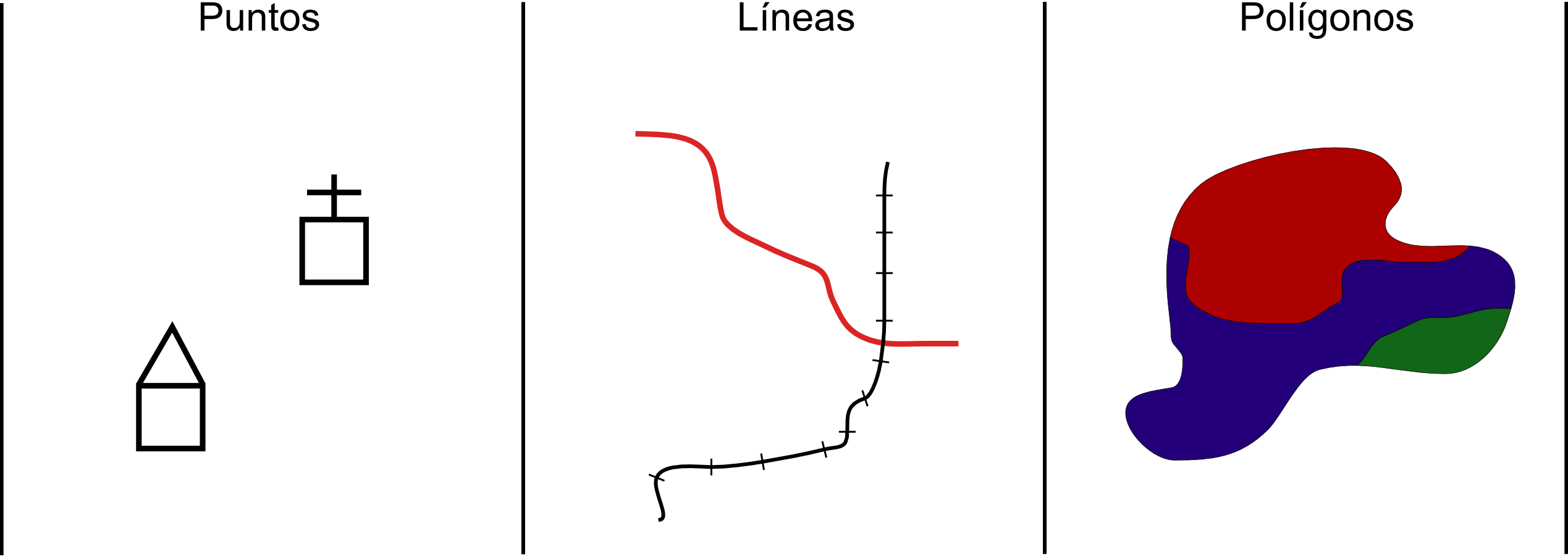
• Nominal . La información de tipo nominal se representa adecuadamente utilizando la variable visual forma. Lo que representamos responde principalmente a la pregunta qué en lugar de a la pregunta cuánto , y está más relacionado en cierto modo con la cartografía base que con la cartografía temática. El uso de símbolos, es decir, de la variable visual forma, para elementos puntuales o lineales es una solución muy eficaz y habitual en este caso. Para el caso de representar áreas puede emplearse la variable visual color y emplear distintos tonos, o bien la textura (Figura \ref{Fig:RepresentacionInfoNominal}). Como dijimos en su momento, los tonos no presentan un orden (aunque citamos que pueden hacerlo si existe alguna lógica en la sucesión de estos), pero este no es necesario para este tipo de variables. La única propiedad que es de interés en este caso es la selectiva. La información alfanumérica se trata a efectos de representación del mismo modo que la de tipo nominal.

• Ordinal . A diferencia de la información nominal, en la información ordinal los valores definen un orden, por lo que la propiedad ordenada es necesaria para poder aplicarla a este caso.
• Intervalos y razones . Tanto intervalos como razones son tipos de información con más posibilidades que las anteriores, y en las que el número de valores que encontramos a la hora de representar un fenómeno es habitualmente más elevado. Frecuentemente, estos valores son de tipo real (no enteros), por lo que es además necesario agruparlos en clases, como veremos en un próximo apartado. Como en el caso anterior, pueden emplearse todas las variables visuales que presenten la propiedad ordenada. No debe olvidarse, no obstante, que la propiedad de mostrar el orden en términos de cantidades o proporciones, que denominábamos cuantitativa, es exclusiva del tamaño, siendo este la variable visual más adecuada para representar correctamente este tipo de información y que al visualizar el símbolo correspondiente pueda estimarse el valor representado de forma intuitiva.

$$\label{Fig:ResumenRepresentacionTiposInformacion}$$

En resumen, podemos condensar este apartado con una rápida «receta» de aplicación general (aunque siempre con excepciones, ya que la representación y simbolización contiene, no olvidemos, elementos subjetivos), según los siguientes puntos:

• Para las variables cualitativas se emplean las variables visuales color, forma y textura, en la medida que sea posible según el tipo de objeto geométrico a simbolizar.
• Para las variables cuantitativas, el valor del color y el tamaño son las más adecuadas, siendo esta última la única que permite transmitir toda la información en el caso de variables de tipo razones. El tono de color puede emplearse, pero debe escogerse una gama de tonos que presente algún tipo de lógica que permita establecer un orden.

En la figura \ref{Fig:ResumenRepresentacionTiposInformacion} se muestra un cuadro con estas breves ideas.

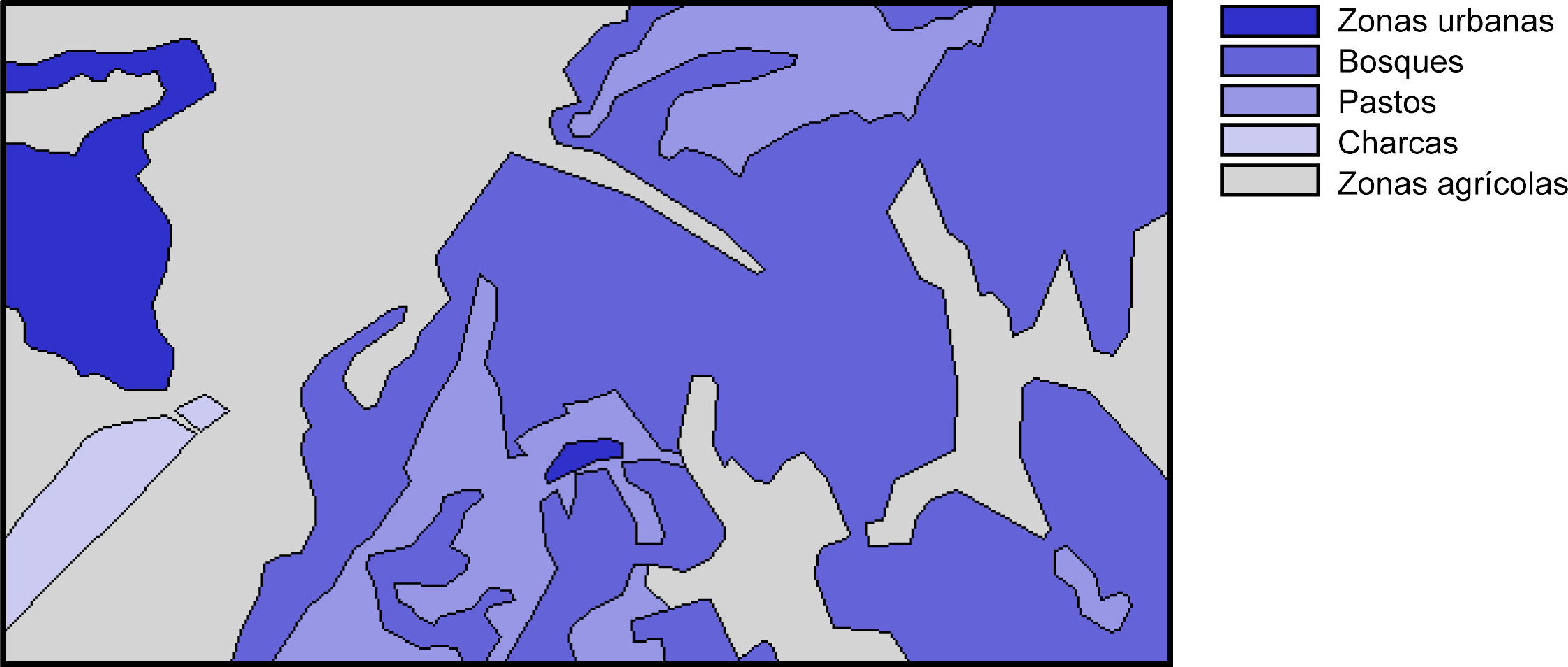
Por último, es de interés señalar que, aunque los niveles de organización de las variables visuales expresan a su vez unas posibilidades crecientes (es decir, con una variable como el valor o el tamaño podemos expresar todo lo que el tono puede transmitir, ya que están en un nivel superior), ello no implica necesariamente que el uso de una variable de un nivel superior es mejor que otra de uno inferior. Podemos ver esto claramente en la figura \ref{Fig:MalUsoValor}. En ella se ha utilizado la variable valor para representar un mapa con información cualitativa. Puesto que el valor tiene la propiedad ordenada, esto puede inducir a pensar que existe algún orden en la variable representada (tipos de suelo en este caso). Además, y debido a que el valor es disociativo, algunos elementos son más llamativos, lo que puede asociar una falsa preponderancia a la clase a la que representan.

Razonamientos similares se pueden aplicar para el caso particular de capas con variables de tipo verdadero/falso. En estas, deben emplearse colores de similares características, de forma que no exista posibilidad de interpretarlos erróneamente y asociar a alguna de las opciones la idea de ser «mejor» que la contraria. Transmitir la información no es lo único que se busca, sino también hacerlo sin que aparezcan posibles sesgos a la hora de interpretarla.

$$\label{Fig:MalUsoValor}$$

Creación y asignación de clases

En el caso de trabajar con información de tipo intervalos o razones, simbolizar cada uno de los valores de una forma distinta supone la necesidad de emplear un número muy elevado de simbologías distintas. Esto puede complicar la interpretación del mapa, especialmente si se lee este junto a su leyenda correspondiente, ya que identificar una simbología concreta en esta es complejo y resulta fácil equivocarse. Asimismo, con un número elevado de simbologías, las diferencias entre estas son pequeñas, por lo que también es complicado separar unas de otras y percibir si dos de ellas son distintas o son la misma. Por esta razón, lo habitual es agrupar todo el conjunto de valores disponibles en una serie de categorías, clasificándolos y estableciendo la simbología no en función del valor en sí, sino de la clase a la que pertenece.

La creación de clases para una serie de valores es un problema en el que han de considerarse dos parámetros principales: el número de clases a crear y el criterio a aplicar para establecer los límites de cada una.

Respecto al numero de clases, este debe ser lo suficientemente grande como para no resumir en exceso la información y poder mostrar con un cierto detalle el comportamiento de la variable, pero no demasiado alto para evitar los problemas que aparecían en el caso de no dividir los valores en clases. El número de clases es también función de la variable visual utilizada, ya que algunas resultan más fáciles de diferenciar. En general, el máximo de clases que se distinguen es del orden de 7 u 8, no siendo recomendable establecer un número mayor, con independencia de qué variable empleemos. Esto no quiere decir que deban crearse sistemáticamente 8 clases para cualquier variable y situación, ya que, en función de otros factores, puede resultar de interés elegir un número distinto. De nuevo, no debe perderse de vista la finalidad que va a tener el mapa que estamos diseñando.

Una vez que hemos decidido el número de clases, debemos definir el rango de valores que cubrirá cada una de ellas. Esto debe llevarse a cabo tratando de maximizar la información que se transmite y de aprovechar lo mejor posible la variable visual empleada. Por ejemplo, si esta variable es el valor de un color, debemos tratar que aparezca bien distribuida y que todas las clases tengan un número similar de elementos, para que todos esos valores aparezcan representados en una cantidad similar a lo largo del mapa dedicado a la expansión de contraste en imágenes, encontrarás una idea similar a esta.}.

La conveniencia de usar una u otra definición de clases está, como resulta fácil deducir, ligada a la propia distribución de los valores de la variable, por lo que estudiar estos es fundamental. Un histograma es una herramienta muy útil para llevar esto a cabo.

De entre los métodos que se emplean frecuentemente para la creación de clases de forma sistemática, cabe destacar los siguientes:

• Intervalos iguales . Simplemente se divide el rango cubierto por los valores en $n$ clases de la misma amplitud, siendo esta igual a $\frac{\mathrm{max} - \mathrm{min}}{n}$. Su principal inconveniente es que puede resultar en clases con muchos elementos y otras prácticamente vacías, en especial si la variable tiene una distribución normal o aparecen elementos con valores atípicos ( outliers ), que desvirtúan el significado del máximo y el mínimo a la hora de calcular la amplitud de cada clase.
• Intervalos naturales . Basados en la propuesta de saltos naturales de Jenks [ Jensk1967IYC ], trata de establecer clases lo más homogéneas posibles, disminuyendo la varianza de cada clase. De este modo, se obtienen clases que presentan la máxima variabilidad entre ellas, constituyendo categorías bien diferenciadas unas de otras.
• Intervalos normales . De especial interés para el caso en que la variable presenta una distribución normal. Se toma la media de los valores y se crean los límites de cada clase sumando o restando a esta la desviación típica o un múltiplo de esta.
• Intervalos por percentiles . Utilizando percentiles pueden crearse clases de tal modo que todas ellas contengan el mismo número de elementos. Por ejemplo, los cuartiles dividirán el rango de valores en cuatro clases, cada una de ella con igual numero de elementos. En este caso, los límites de separación de clases se encontraran en los percentiles del 25, 50 y 75 por cien, respectivamente. Pueden aplicarse también los percentiles no sobre la variable que se representa, sino sobre la superficie que ocupan sus distintos valores. Se tiene de este modo los percentiles de superficie , que crean $n$ clases, todas ellas representadas en el mapa por una misma superficie.
• Intervalos en progresión . Pueden emplearse progresiones como la aritmética o la geométrica para crear las clases, en caso de que los valores de la variable a representar muestren un comportamiento según alguna de estas progresiones.

Una comparación visual del resultado de aplicar algunos de los métodos anteriores se muestra en la figura \ref{Fig:TiposIntervalosClases}

$$\label{Fig:TiposIntervalosClases}$$

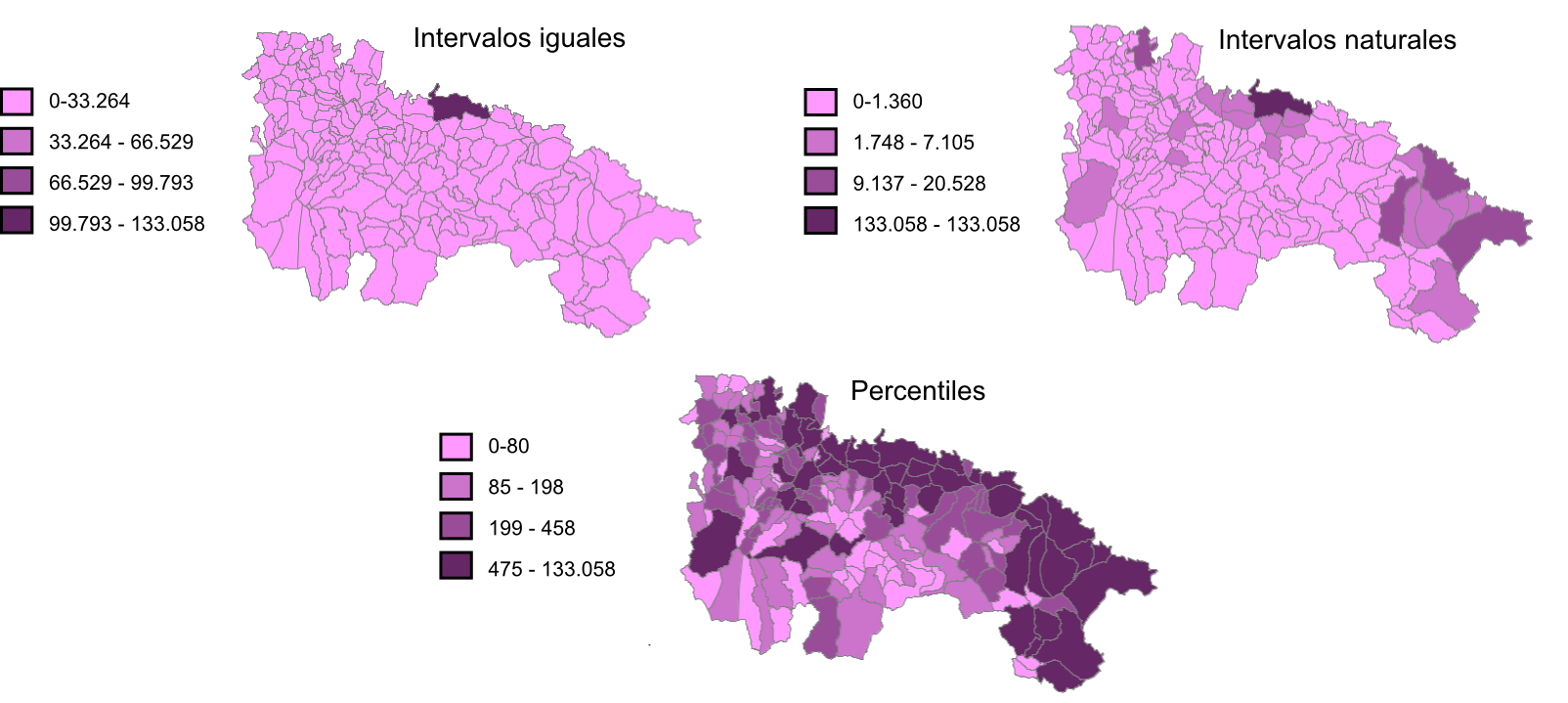
Junto a lo anterior, pueden utilizarse transformaciones de los valores previas a su asignación a una clase, para después clasificar el valor transformado. Una transformación logarítmica es habitual para el caso de valores distribuidos irregularmente, con muchos de ellos en un rango dado y unos pocos en un rango alejado de este. Aplicando un logaritmo (generalmente de base 10), los valores transformados pueden mostrar, por ejemplo, una distribución normal, siendo entonces posible aplicarles una simbolización mediante intervalos normales.

Aunque resulta práctico definir las clases utilizando alguna de las metodologías anteriores, pueden igualmente establecerse límites de clase arbitrariamente según se considere oportuno en función de la distribución de los valores. Por ejemplo, si existen saltos importantes en esta y quiere reseñarse este hecho, pueden incluirse explícitamente como límites de los intervalos. Asimismo, pueden incorporarse valores particulares que sean de importancia para la variable representada. Esto puede verse claramente en el ejemplo de la figura \ref{Fig:TintasElevacion}

$$\label{Fig:TintasElevacion}$$

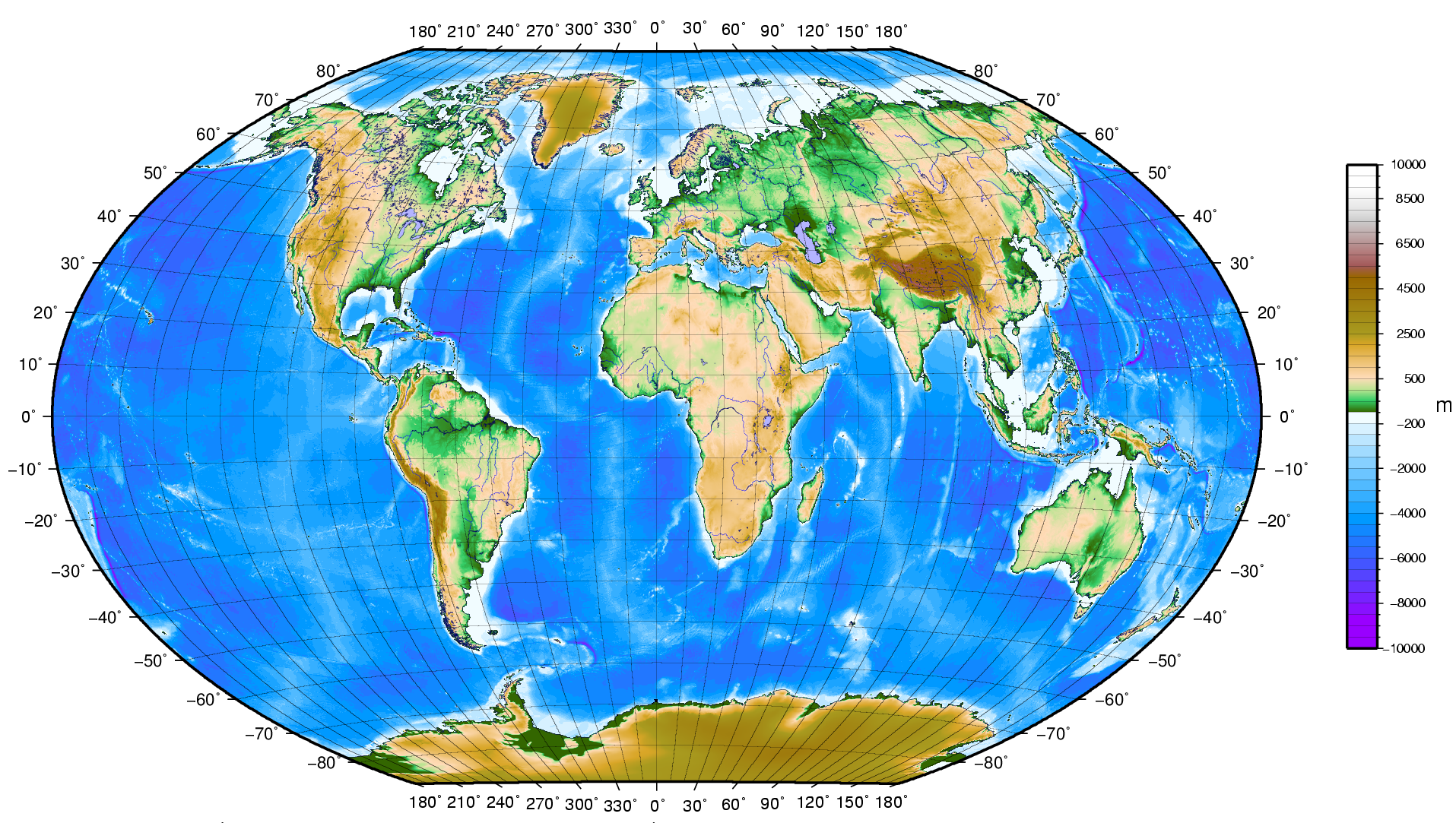
Para el caso mostrado, en el cual se representa la elevación, es interesante diferenciar los valores positivos (sobre el nivel del mar) de los negativos (zonas por debajo del nivel del mar y, especialmente, batimetría del fondo marino). El cero es un valor que puede o no aparecer de modo natural como límite de clase al analizar los datos de elevación, pero que se incorpora por su importancia.

El mapa de la figura presenta además un caso particular por otras razones, ya que utiliza el color como variable ordenada, pese a que dijimos que normalmente no posee tal propiedad. No obstante, este es uno de esos casos en que sí existe un orden fácil de percibir, ya que los colores escogidos están pensados para ser identificados con distintas zonas altitudinales. Las zonas de batimetría se representan en tonos de azul, por lo que en ese tramo se está empleando realmente la componente del color que denominábamos valor. Para las restantes, se comienza en el verde (zonas bajas donde crece vegetación que es de ese color), seguido del marrón (zonas altas sin vegetación) y después el blanco (zonas elevadas que se pueden asociar a nieve). La división en esos tramos se hace empleando el valor igualmente. Esta asociación de conceptos tan básica (y no necesariamente muy real, pero sí conocida y compartida por todo el mundo) permite crear un orden y capacitar a la variable visual color para emplearse a la hora de representar una variable de tipo intervalo como es la elevación.

La presencia del valor cero como punto que define dos mitades (elevaciones sobre el nivel del mar o por debajo de este) hace que los datos de elevación tengan, en lo que a su simbolización respecta, un esquema de tipo divergente . Este tipo de esquemas aparecen cuando la variable presenta algún valor crítico con un significado particular, dividiendo el conjunto de valores en grupos que pueden considerarse independientes. Es habitual emplear un color de valor bajo (esto es, un color claro) en las cercanías del punto crítico, y aumentar el valor a medida que nos acercamos a los extremos tanto por encima como por debajo de este punto. Cada mitad, a su vez, suele representarse con colores que presentan un fuerte contraste entre sí, para de este modo indicar que cada una de ellas representa una realidad bien distinta de la otra.

Los esquemas no divergentes para variables cualitativas se dice que son de tipo secuencial .

Debe reseñarse que, en el caso de establecer las clases en función de los datos, tal y como sucede al aplicar los métodos que hemos descrito, la simbolización no será adecuada para realizar comparaciones con otros mapas. Un mismo valor puede simbolizarse con colores distintos en dos mapas dados, ya que la clase a la que pertenece depende del resto de valores en su conjunto, por lo que no tiene sentido una comparación visual. Por el contrario, si el intervalo se define sin considerar los valores particulares del conjunto representado (como en el mapa de elevaciones anterior), el mismo color en dos mapas sí que implica un mismo rango de valores, con lo que pueden efectuarse comparaciones.

Si quieres experimentar con la definición de clases y la asignación de colores a estas, una herramienta de enorme valor es la que encontrarás en la pagina Web http://www.colorbrewer.org . Úsala no solo para probar ahora todo lo explicado en este capítulo, sino también cuando tengas que crear tus propios mapas. Elegir un conjunto adecuado de colores y clases no es una tarea sencilla, y una herramienta así puede aportar mucho valor a tus mapas si la empleas correctamente junto a las propias funcionalidades del SIG que estés utilizando.

Elementos del mapa. Composición

Un mapa no es solo una colección de gráficos que representan objetos o valores del mundo real a una escala dada, sino que para ser verdaderamente completo requiere completarse con otra serie de elementos adicionales. Es decir, el mapa en sí no es solo lo que se deriva de la representación de la información geográfica y su simbolización, sino un conjunto de elementos dispuestos de forma óptima, entre los cuales, eso sí, resulta de particular relevancia aquel que contiene la información geográfica como tal.

Igual de importante que simbolizar de manera correcta la información geográfica es situar adecuadamente los distintos elementos del mapa, ya que estos están pensados también, al igual que la propia simbología, para facilitar la interpretación de la información y hacer esta más comprensible.

Los siguientes son los elementos fundamentales que podemos emplear para componer un mapa (Figura \ref{Fig:ElementosMapa}):

$$\label{Fig:ElementosMapa}$$

• Nombre o título . Imprescindible para conocer qué información muestra el mapa.
• Autor . La persona u organismo que ha creado el mapa debe aparecer indicada en algún punto de este.
• Otra información sobre el mapa . Por ejemplo, la relativa al sistema de referencia empleado o la fecha de su creación, entre otras.
• Canevás . El canevás nos indica dónde dentro de la superficie terrestre se encuentra aquello que el mapa representa, y provee la referencia geográfica para sus elementos. Asimismo, complementa a la escala para la estimación visual de distancias y medidas. Es más necesario en caso de escalas bajas, aunque se añade con independencia de la escala.
• Leyenda . Aunque se ha de tratar de utilizar una simbología lo más expresiva posible, no toda la información puede incorporarse en el mapa, y es necesario acompañarlo de una leyenda. Esta ha de ser también fácil de interpretar y lo más clara posible. Una leyenda demasiado extensa o de difícil comprensión probablemente nos indica que la simbología escogida es mejorable. La leyenda y el mapa en sí forman un todo, por lo que no deben separarse mediante un cuadro, salvo en el caso en que el mapa cubra todo el área del lienzo y no sea fácil separar visualmente de forma clara ambos elementos.
• Norte . Aunque habitualmente se presupone la orientación Norte-Sur, no siempre ha de ocurrir así, y una aguja apuntando al norte o una rosa de los vientos sirve para aclarar la orientación del mapa. Es de reseñar que la orientación no ha de ser constante para todos los puntos de un mapa, estando esto en relación con el tipo de sistema de coordenadas y la proyección empleada. Por ejemplo, en el mapa mundial de la figura \ref{Fig:TintasElevacion}, el Norte se sitúa hacia arriba de la hoja solo en el centro. Si nos encontramos en la parte izquierda del mapa la dirección del Norte no es la misma. El canevás, que contiene los paralelos y meridianos, será en este caso la referencia fiable en lo que a orientación respecta.
• Escala . La escala debe indicarse tanto de forma numérica como gráfica, de modo que puedan realizarse cálculos y estimar visualmente distancias entre puntos dados del mapa.
• Localizador . Un localizador provee un elemento visual para situar el mapa en un contexto geográfico más amplio, de modo similar al canevás. Es de especial interés en el caso de series de mapas, para establecer la relación entre el presente y los restantes dentro de la misma serie. En este caso, el localizador sirve como mapa índice.
• Mapas de detalle . Cuando resulta necesario mostrar una cierta zona del mapa con mayor detalle y a una escala mayor, se puede incluir un mapa correspondiente a esa zona como un enclavado dentro del mapa principal. Se debe señalar asimismo sobre este último la zona a la que corresponde el mapa de detalle.

Aunque en un mapa en sentido clásico deben incorporarse todos o la gran mayoría de los anteriores elementos, cuando trabajamos con representaciones dentro de un SIG la situación es distinta y se puede prescindir de una buena parte de ellos. Por ejemplo, y dado el carácter menos persistente de la representación en pantalla, añadir el nombre del autor carece la mayoría de las veces de sentido. Información tal como la procedencia de los datos que estamos visualizando resulta de más interés que el autor del mapa, pero lo correcto es consultar esta en los propios datos, que deberían contenerla de algún modo (vimos esto en el capítulo Metadatos ).

La escala es adecuado mostrarla de forma numérica, pero no tanto en su versión gráfica, ya que dentro de un SIG encontramos herramientas que nos permiten medir con total precisión distancias y áreas, y una escala gráfica carece de utilidad en este contexto. Por su parte, el localizador es mejor que el canevás para definir el contexto, ya que muchas aplicaciones SIG incorporan incluso un localizador interactivo sobre el que puede operarse para cambiar el encuadre del mapa.

En lo que respecta a la forma de disponer los elementos sobre el lienzo que un mapa conforma, la premisa fundamental es maximizar la claridad y aprovechar de la mejor forma posible el espacio disponible. La figura \ref{Fig:AprovechamientoEspacioMapa} muestra un claro ejemplo de cómo un adecuado uso del espacio en el mapa, evitando que existan zonas en blanco que no comunican ninguna información, mejora notablemente la calidad del mapa.

$$\label{Fig:AprovechamientoEspacioMapa}$$

Asimismo, es importante que el diseño del mapa recalque su propósito, haciendo énfasis en los aspectos más relevantes para cumplir este.

Aunque el objetivo principal del diseño cartográfico es crear un mapa útil y no un mapa bonito, no cabe duda que una cierta preocupación por el aspecto estético es recomendable, ya que también contribuirá a una mejor interpretación de la información del mapa. Este es un aspecto subjetivo y con una componente principalmente artística, aunque también pueden aportarse algunos elementos metodológicos de carácter más sistemático. Uno de ellos utilizado frecuentemente es el empleo de la proporción áurea para dimensionar los elementos del mapa. Comenzando por las dimensiones del propio lienzo, puede aplicarse a las de los restantes componentes, tales como la leyenda en caso de estar situada en un cuadro aparte, o el cuadro que contiene el nombre del mapa y otra información adicional.

Los conceptos que deben manejarse a la hora de elegir las características de los elementos del mapa y su emplazamiento derivan de la percepción visual, disciplina que ya vimos en el capítulo anterior. A continuación tienes algunas ideas adicionales sobre percepción visual que deben aplicarse a la composición de mapas. Si deseas ampliar estos conceptos, una buena referencia sobre percepción visual desde el punto de vista del arte es [ Arnheim1986Paidos ].

• El documento cartográfico tiene dos centros. Un centro geométrico y uno óptico. Este último se sitúa por encima del geométrico, aproximadamente a un 5% de la altura total del documento. Los elementos del mapa se deben disponer alrededor del centro óptico.

• Los elementos en la parte superior del mapa tienen una mayor importancia, así como los situados en la parte izquierda. Es en estas zonas donde deben situarse los elementos más importantes sobre los que se quiera centrar la atención.

• La atención del lector del mapa va desde la esquina superior izquierda hasta la inferior derecha, pasando por el centro óptico. Los elementos importantes deben situarse en esta línea, para que su posición se corresponda con los movimientos naturales de la vista.

• Debe tratarse de crear un mapa que sea visualmente equilibrado. El equilibrio visual es el resultado del peso que cada elemento tiene y su posición, así como su orientación. Estos pesos deben repartirse adecuadamente por todo el lienzo del mapa. El peso de un elemento depende de múltiples factores, entre ellos los siguientes:
  • Posición. Los elementos tiene más peso en la derecha que en la izquierda, y más en la parte superior que en la inferior. El peso aumenta al aumentar la distancia al centro del documento.
  • Tamaño. Mayor tamaño implica más peso.
  • Color. Los colores brillantes tienen más peso que los oscuros. El tono rojo tiene más peso que el azul.
  • Aislamiento. Los elementos aislados tienen más peso que aquellos rodeados por otros.
  • Forma. Las formas regulares tienen más peso que las irregulares. Cuanto más compacta sea la forma, también tendrá más peso.
  • Dirección. Algunos elementos pueden tener una dirección que «dirija» la atención hacia otros, concediéndoles peso (por ejemplo, una flecha que señale a un elemento, haciendo que llame más la atención),

Las ideas acerca de la composición y el equilibrio del mapa se han de aplicar a todo el documento cartográfico (es decir, al que contiene todos los elementos citados anteriormente), así como a la parte de este que representa la información geográfica. Es importante seleccionar adecuadamente el área geográfica cubierta para que la información relevante que se muestra acerca de esta conforme un conjunto equilibrado y siga a su vez las indicaciones mencionadas.

Recordar, por último, que la composición del mapa implica una organización horizontal (plana) de sus elementos, pero existe asimismo una organización vertical. Esta viene definida por la jerarquía existente, sobre la cual ya se comentaron algunas ideas en el apartado AyudasPercepcion . Estas ideas deben aplicarse igualmente en la composición del mapa, para conjuntamente lograr un documento equilibrado en el que quede claro qué elementos son los de mayor importancia, y en el que pueda accederse con facilidad a la información que contienen.

Tipos de mapas temáticos

Los mapas temáticos representan la mayor parte de los creados en un SIG, por lo que resulta necesario ver en detalle las formas en las que pueden presentarse. Existen diversas alternativas en función del tipo de elemento que se pretenda simbolizar o las características de la variable tratada, y la elección de una u otra supondrá una diferencia importante en el mapa obtenido y en su uso posterior. En un mismo mapa pueden combinarse varias de estas formas, especialmente si se pretende representar más de una variable, en cuyo caso la combinación debe buscar la máxima claridad en la representación de todas ellas.

En este apartado detallaremos los siguientes tipos de mapas temáticos: mapas de símbolos proporcionales, mapas de densidad de puntos, mapas de coropletas, y mapas de isolíneas. Todos ellos se utilizan para la representación de variables cuantitativas.

Mapas de símbolos proporcionales

Un mapa de símbolos proporcionales representa variables cuantitativas a través de símbolos cuyo tamaño esta en relación con el valor a representar de dicha variable. Es decir, emplea la variable visual tamaño, que como ya hemos visto es la única que presenta la propiedad cuantitativa. La forma de los distintos símbolos es siempre la misma, y por simplicidad lo más frecuente es utilizar como símbolo base el círculo, aunque puede utilizarse cualquier otro, e incluso símbolos de tipo lineal (barras).

Puesto que el tamaño es el elemento que diferencia a los distintos símbolos y el que transmite la información cuantitativa, su elección es crucial para la creación de un buen mapa de este tipo. La elección de un tamaño implica elegir uno mínimo y uno máximo, correspondientes a los valores mínimo y máximo de la variable en el mapa. Entre estos se situarán los distintos tamaños correspondientes al resto de posible valores que toma la variable.

Existe, claramente, una relación entre el tamaño máximo y el mínimo, ya que se define una relación de escalado de los distintos valores. Este escalado es distinto para símbolos lineales que para símbolos de área, ya que la percepción de la relación entre ellos es distinto según el tipo de símbolo empleado. En ambos casos, el escalado debe ser coherente con el valor que se representa, de tal modo que si el usuario del mapa percibe que el tamaño de un símbolo es el doble que el de otro, los valores de ambos símbolos estén igualmente en esa proporción.

Para conseguir esto se ha de seleccionar el tamaño asociado al valor de uno de los extremos. Esto se hará con un criterio puramente gráfico, de tal modo que, si por ejemplo establecemos el tamaño máximo, este no sea excesivo y a la hora de representar el símbolo correspondiente en el mapa ocupe demasiado espacio y existan solapes. Debe evitarse asimismo que el tamaño mínimo sea demasiado pequeño y no se aprecie el símbolo con claridad. Una vez hecho esto, se establece una relación lineal, de tal forma que podemos calcular el tamaño correspondiente a todo valor. Si un valor de 100 se corresponde con una barra de una altura de 10 mm, entonces un valor de 200 se representara mediante una barra de 20 mm, y así sucesivamente.

Para el caso de símbolos superficiales, no obstante, el escalado no debe hacerse en función de un parámetro lineal (por ejemplo, el radio en el caso de emplear círculos), sino respecto a la propia superficie. Es decir, si un valor de 100 se representa con un circulo de radio $r$, el valor 200 no se representará mediante un círculo de radio $r'=2r$, sino con una de tal radio que la superficie sea el doble del primero. En este caso, el radio buscado sería $r' = \sqrt{2}r$.

El escalado de símbolos se puede dar de forma continua, de tal modo que cada valor se representa con un símbolo de un tamaño calculado según la idea anterior, empleando el valor exacto para el escalado. No obstante, la capacidad de diferenciar visualmente tamaños distintos e interpretar la relación entre ellos es limitada, por lo que suele resultar más conveniente efectuar un escalado discreto. Es decir, crear clases y asignar a un valor no un símbolo del tamaño exacto que le correspondería, sino el asignado al valor que define a la clase, habitualmente el centro de esta.

Tanto las barras como los círculos pueden sectorizarse, mostrando una división en subclases del valor total que representan. Para el caso de la población, podrían mostrarse las proporciones que corresponden a hombres y mujeres. Este tipo de representaciones, no obstante, son a veces difíciles de interpretar en su conjunto, por lo que resulta más adecuado crear varios mapas que muestren esa misma información por separado, en lugar de conjuntamente en uno único.

Aunque la variable visual tamaño presenta la propiedad cuantitativa, la percepción de la relación de tamaño no es perfecta y existe una cierta imprecisión. Esta se debe a muchos factores, como por ejemplo el hecho de que los símbolos situados alrededor de uno dado pueden afectar a la percepción de su tamaño. Por esta razón, es importante para facilitar la correcta interpretación de un mapa de símbolos graduados el mostrar en la leyenda la relación entre los distintos tamaños de los símbolos y sus valores. Para el caso habitual de emplear círculos, esto puede llevarse a cabo mediante elementos gráficos como los mostrados en la figura \ref{Fig:EjemplosLeyendaSimbolosProporcionales}

$$\label{Fig:EjemplosLeyendaSimbolosProporcionales}$$

El uso de un escalado lineal en el que se conserve la propiedad cuantitativa resulta en ocasiones inapropiado debido a la distribución de los valores. Por ejemplo, para representar el mapa de la figura \ref{Fig:TiposIntervalosClases}, este esquema no es adecuado, ya que una de las zonas presenta un valor de la variable muy superior a la del resto (puede verse esto claramente en la representación por intervalos iguales), lo cual requeriría el uso de un símbolo desproporcionadamente grande. Si se usan clases iguales, la mayoría de los valores entrarían en una de ellas, por lo que no se transmitiría bien la distribución de estos. En este caso, se debe emplear un esquema de clases distinto, aunque así la proporción de tamaños no permita visualmente estimar las cantidades. Es decir, los tamaños de los símbolos nos indican que hay más cantidad en una zona que en otra, pero no podemos solo con ellos saber cuánto más hay. Los mapas elaborados de esta forma se conocen como mapa de símbolos graduados . En estos mapas, la importancia de la leyenda es aún mayor si cabe, ya que es la encargada de explicar el significado de cada tamaño, y sin ella la información de la que disponemos es mucho menor.

El mapa de la figura \ref{Fig:ElementosMapa}, que mostramos al presentar los distintos elementos del mapa, es un ejemplo mapa de símbolos graduados.

Mapas de puntos

Los mapas de puntos se emplean especialmente para la representación de variables que representen algún tipo de cantidad, tales como la población, el gasto medio por persona o la producción de un determinado cultivo. Estas cantidades se representan mediante la repetición de puntos, en numero proporcional a su magnitud. Cada uno de esos puntos representa un valor unitario, y el conjunto de ellos sobre la zona en cuestión suma la cantidad total a representar. Los puntos tienen todos la misma forma y tamaño, a diferencia de lo que vimos en el caso de los símbolos proporcionales.

Los mapas de puntos transmiten de forma muy eficaz los valores que representan, obteniéndose estos por el mero recuento, aunque visualmente permiten una estimación inmediata y pueden compararse entre las distintas zonas del mapa. Por esta razón, son especialmente adecuados para variables discretas más que para continuas, aunque también pueden emplearse para estas últimas.

Aunque podrían crearse con cualquier otro símbolo, ya que es la repetición de este la que transmite la información, lo más habitual es el empleo de puntos, de ahí el nombre genérico que se les da.

Tres son los aspectos que deben tenerse en cuenta a la hora de elaborar un mapa de puntos: el valor de cada punto (es decir, cuántas unidades de la variable representa cada punto), su tamaño y su posición.

Si los valores de la variable que se manejan son bajos, se puede establecer como valor del punto la unidad. Es decir, un punto representa sobre el mapa un habitante en el caso de un mapa de población. No obstante, con valores altos (como en el caso de la población) esto da lugar a un número demasiado elevado de puntos que saturan el espacio del mapa y no transmiten adecuadamente la información. Por ello, cada punto debe representar un número mayor de elementos de la variable representada, de tal modo que no aparezcan en demasía en el mapa, solapándose unos con otros.

Si el valor escogido es demasiado alto, aparecerán pocos puntos en el mapa, y este puede quedar poco expresivo y no transmitir la distribución de la variable. Debe, por tanto, escogerse un valor adecuado que equilibre la presentación de los puntos sobre el mapa. Este valor se representará en la leyenda para su interpretación, habitualmente en forma de texto, escribiendo por ejemplo, que «un punto equivale a 1000 habitantes».

La elección del tamaño del punto debe garantizar la buena visibilidad de este, al tiempo que no debe ser excesivamente grande para que no ocupe demasiado espacio y dificulte la visión de otros. Obviamente, el tamaño óptimo está en relación con el valor unitario escogido, y ambos parámetros deben establecerse conjuntamente para lograr la combinación más adecuada.

Por último, la posición del punto es de gran importancia para transmitir la información correcta y no dar lugar ambigüedades o incorporar errores conceptuales. Si no disponemos de información adicional y solo tenemos el valor correspondiente a una zona dada, los puntos se han de disponer de forma regular ocupando toda la superficie de la zona. Si, por el contrario, sabemos algo más acerca de la distribución de la variable, debemos emplear esa información para emplazarlos de forma más realista. Si, por ejemplo, la zona corresponde a una provincia y sabemos la localización de la principal ciudad dentro de ella, es más lógico situar más puntos cerca del emplazamiento de esa ciudad que en otras partes de la provincia, ya que una mayor parte de la población estará allí.

Otro aspecto a considerar es el significado de la variable que se representa y la posibilidad o no de que aparezca en las distintas localizaciones de los puntos. Si la variable es, por ejemplo, el numero de ejemplares avistados de un determinado ave acuática, situar los puntos sobre zonas urbanas o de bosque no tiene sentido, ya que dan a entender que ahí hay presencia de esa especie (tantos ejemplares como los puntos en cuestión indiquen), algo que es falso.

En los dos casos anteriores va a resultar necesario «mover» los puntos a su localización más correcta, algo que, habitualmente, no resulta posible con los mecanismos automatizados de que dispone un SIG. El chequeo del mapa creado resulta, por tanto, imprescindible para comprobar que existen puntos en posiciones erróneas. El uso de herramientas externas tales como programas de diseño gráfico, según vimos en el capítulo Introduccion_visualizacion , es una solución para retocar los mapas creados y obtener una distribución de los puntos más correcta.

La imagen \ref{Fig:MapaPuntos} muestra un ejemplo de un mapa de puntos.

$$\label{Fig:MapaPuntos}$$

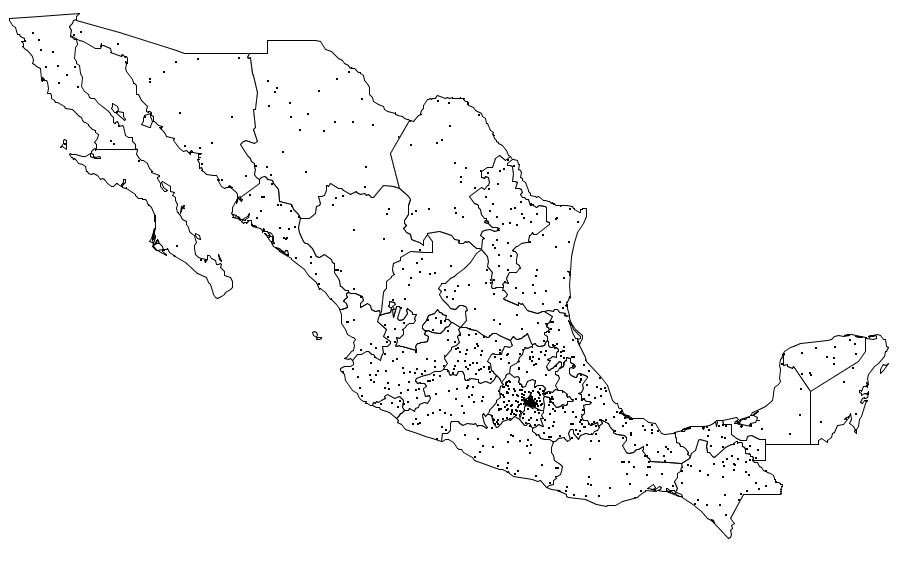
Mapas de isolíneas

Los mapas de isolíneas están entre lo más usados para la representación de información cuantitativa, en particular cuando se trata de variables continuas. Se utilizan habitualmente para representar campos escalares, y constituyen una forma muy efectiva de incorporar esta información en un mapa, ya que pueden combinarse con otros tipos de mapas y de información, debido a que, al representarse únicamente mediante líneas, permite la presencia de otros elementos dentro del mapa sin resultar estas obstrusivas.

Un mapa de isolíneas está formado por un conjunto de líneas, cada una de las cuales une puntos que presentan el mismo valor de la variable. Estas líneas no pueden cruzarse, ya que ello significaría que en un punto se presentan dos valores. El caso más típico de mapa de isolíneas son las curvas de nivel que aparecen el un mapa topográfico, indicando la elevación del terreno. Otras variables que habitualmente se representan mediante curvas de nivel son la temperatura (en cuyo caso, las líneas se denominan isotermas ), la presión ( isobaras ) o el tiempo ( isocronas ). En el caso de las curvas de elevación, estas se conocen como isohipsas , aunque resulta mucho más habitual denominarlas simplemente curvas de nivel, nombre que se emplea también por extensión como sinónimo general de isolíneas.

Para una variable continua, los valores que esta puede tomar son infinitos, por lo que el número de isolíneas que pueden trazarse también lo es. Por ello, es necesario seleccionar qué isolíneas se desea representar, estableciendo clases y representando tan solo los límites de estas. A pesar de esta división, no resulta habitual un análisis complejo a la hora de establecer la distintas clases, tal y como se detalló en el apartado CreacionClases . En su lugar, se emplean en la gran mayoría de casos intervalos iguales, siendo el tamaño de cada clase (el rango de valores que cubre) el único parámetro a definir. Este parámetro es lo que se conoce como equidistancia en un mapa de curvas de nivel.

La construcción de un mapa de curvas de nivel implica estimar el trazado de estas a partir de valores puntuales, lo cual coincide con lo que vimos en el capítulo Creacion_capas_raster acerca de los distintos métodos de interpolación. Dentro de un SIG, el procedimiento a seguir será calcular una capa ráster a partir de valores puntuales, y después crear las isolíneas a partir de esta capa según lo visto en el apartado Isolineas , para una equidistancia dada.

A la hora de simbolizar las isolíneas, y con independencia de su tipo, la variable visual tamaño es la única que suele emplearse, en particular para señalar aquellas líneas que representan un valor múltiplo de una determinada cantidad y hacer así más fácil la lectura del mapa. Estas líneas son lo que se conoce como curvas directrices . Por ejemplo, en un mapa topográfico con curvas de nivel con una equidistancia de 100 metros, es habitual establecer curvas directrices cada 500 metros. Todas aquellas curvas cuyo valor asociado sea múltiplo de 500 se representan con un trazo más grueso para que puedan localizarse rápidamente.

$$\label{Fig:Isolineas}$$

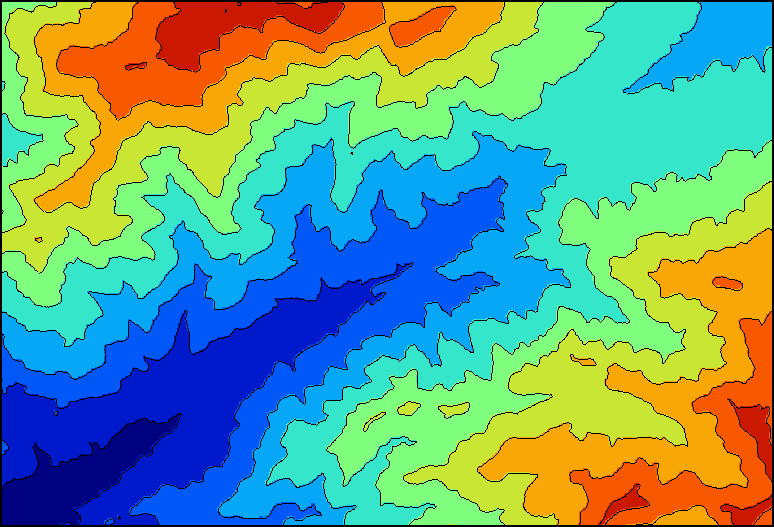
El uso del color o la textura en las líneas no es habitual como simbología, ya que simbolizar los valores de cada una a través de las variables visuales resulta en este caso menos práctico. Lo normal es etiquetar cada una de ellas con el valor concreto (con texto sobre la línea), y aprovechar el hecho de que dos líneas consecutivas están separadas siempre una magnitud igual al tamaño de la clase (la equidistancia), lo cual aporta un importante contexto en lo que a los valores se refiere.

Una forma particular de representar las isolíneas mediante color es hacerlo no sobre las líneas, sino sobre las zonas que median entre ellas. Es decir, representar la clase en lugar del límite de clase. Este tipo de mapas se asemeja al mapa de coropletas (que veremos seguidamente), tratándose más de un mapa de áreas que de líneas, por lo que se conoce como de isocoropletas . Ambos tipos de representación, mediante áreas y mediante líneas, pueden combinarse en un único mapa.

En la figura \ref{Fig:Isolineas} puede verse un ejemplo de mapa de isocoropletas.

Mapas de coropletas

Los mapas de coropletas se utilizan de manera muy habitual en un SIG, y hemos visto ejemplos de ellos en otros puntos de este y otros capítulos. Por ejemplo, los mapas de la figura \ref{Fig:TiposIntervalosClases} son todos ellos mapas de coropletas.

En un mapa de coropletas se tiene una serie de áreas definidas, cada una de las cuales posee un valor de una variable. Este valor de la variable afecta a todo el área y es el que se representa por medio de alguna variable visual, normalmente el color a través de su componente valor. Las zonas definidas por cada área tienen un significado arbitrario, no relacionado con la variable asociada. Muy frecuentemente, se utilizan limites administrativos o de gestión para este propósito. Cada área conforma una unidad espacial, y el valor asociado a ella resume la variable dentro de dicho área.

Precisamente por esta generalización que se da al representar mediante un único valor la variable dentro de cada unidad, los mapas de coropletas adolecen de ciertos inconvenientes, siendo los dos siguientes los principales:

• Sensación de cambio brusco en los límites entre áreas . Al existir una transición abrupta entre unidades, un mapa de coropletas puede transmitir la idea de que en esa frontera los valores de la variable cambian bruscamente, ocultando la continuidad de la variable en caso de existir esta.
• Homogeneidad dentro de cada área . La variación dentro de cada área no se recoge, con lo que se pierde una parte de la información. El uso de unidades menores soluciona en parte este problema, aunque puede hacer el mapa más complejo de interpretar y puede desvirtuar la información (recordemos aquí todo lo que vimos en el capítulo Analisis_espacial y los conceptos tales como el Problema de la Unidad de Área Modificable). Al mismo tiempo, las unidades pueden tener su significado particular, como por ejemplo tratarse de divisiones administrativas, con lo que el uso de otras distintas altera la información que se pretende transmitir.

Igualmente, debe considerarse que, en el caso de valores no normalizados, las coropletas pueden transmitir una información equivocada. Por ejemplo, si una variable representa un conteo, tal y como la población de un conjunto de estados, el uso de coropletas no tiene en cuenta la superficie de cada una de las áreas representadas. Un mismo valor en dos unidades, una de ellas con una superficie mucho mayor a la otra, puede dar la sensación de que poblacionalmente ambas zonas son similares, mientras que puede ser que una tenga una gran densidad de población y la otra esté prácticamente despoblada. El valor que simbolizamos sí está relacionado con el área (a mayor área, encontraremos más habitantes), y sería más adecuado representar esa densidad de población, ya que resulta menos proclive a inducir una interpretación errónea. En general, el uso de coropletas es correcto cuando la variable ha sido normalizada, por ejemplo dividiendo el valor numérico de cada unidad entre la superficie de esta.

En los mapas de coropletas cobra especial importancia la correcta división de clases según hemos detallado dentro de este mismo capítulo. De entre las variables visuales, el color es la usada en la gran mayoría de casos, en particular utilizando su componente valor, y las propias características de las coropletas, en particular las desventajas que ya hemos mencionado, han de considerarse a la hora de establecer cómo hacemos uso de esta variable visual para la simbolización de cada unidad.

Así, debemos tener en cuenta que a la hora de distinguir dos colores con el mismo tono y distinto valor, si estos son muy semejantes solo resulta posible diferenciarlos cuando se sitúan el uno junto al otro, pero no cuando están separados y median entre ellos otros colores distintos. Aunque la variable con la que trabajemos sea continua, el mapa de coropletas no ha de exhibir dicha continuidad, por lo que no podemos contar con ella para elaborar la rampa de valores correspondiente. En un mapa de coropletas, una unidad puede tener a su lado otra con un valor muy distinto sin que entre ellas exista una de valor intermedio, pudiendo producirse un salto de varias clases. Esto tiene como consecuencia que el número de clases que podemos emplear es más reducida, ya que esta separación espacial que puede aparecer en las distintas clases va a dificultar su diferenciación.

De igual modo, el uso del tono queda más restringido, al poder dar lugar a situaciones ambiguas. Por ejemplo, si miramos la leyenda del mapa de la figura \ref{Fig:TintasElevacion} veremos que hay dos clases con un tono blanco. Por una parte, los valores situados cerca del cero (al nivel del mar). Por otro, los situados en la parte superior de la escala, es decir, los que corresponden a mayor elevación. Esto no da lugar a ambigüedad, ya que el primer caso siempre aparecerá cerca de tonos azules, mientras que el segundo se situará cerca de los marrones. No puede ser de otro modo, ya que equivaldría a que las curvas de nivel pudieran cortarse entre sí, lo cual sabemos que no es posible. El contexto de los colores circundantes sirve para eliminar la ambigüedad. En el mapa de coropletas, al no suceder necesariamente así, la ambigüedad permanecería y haría imposible discernir el significado de la simbología. En el caso de las isocoropletas, en la que la contigüidad espacial sí implica también contigüidad de clases, sí pueden utilizarse este tipo de esquemas, como ya vimos en la figura \ref{Fig:Isolineas}.

Por todo lo anterior, el uso de la componente valor es preferible frente al uso del tono a la hora de crear un mapa de coropletas para representar información cuantitativa.

Otros tipos de mapas

Existen muchos otros tipos de mapas, adecuados para representar tipos particulares de información. A pesar de su utilidad, son mucho menos frecuentes, especialmente dentro del ámbito SIG, ya que su implementación no es habitual y no resulta común crearlos con las herramientas usuales de estos. Algunos de estos tipos de mapas que resulta de interés reseñar son los siguientes:

• Mapas dasimétricos . Los mapas dasimétricos tratan de evitar las deficiencias de los mapas de coropletas, en los que los límites de las distintas áreas representadas no tienen relación con la variable con la que se trabaja, siendo limites arbitrarios tales como divisiones administrativas o territoriales. En los mapas dasimétricos las divisiones obedecen a la propia geografía de la variable. El principal inconveniente de estos mapas es el mayor esfuerzo que su preparación exige, así como el mayor conocimiento de la variable que resulta necesario para poder definir las distintas zonas del mapa. Tradicionalmente se han empleado para representar la densidad de población, siendo poco usados para otras variables.
• Mapas de flujo . Los mapas de flujos representan movimientos de algún tipo de elemento, como por ejemplo las exportaciones de un producto o los desplazamientos de tropas en una campaña militar. El mapa de flujo aporta información sobre cómo se produce la distribución del elemento que se desplaza, la proporción o magnitud en que lo hace, así como también la ruta seguida, aunque este último factor no es habitualmente prioritario y suele representar más con carácter esquemático (indicando la relación entre los puntos de partida y destino del movimiento) que como verdadera información geográfica sobre el trayecto en cuestión. Algunos de los mejores ejemplos de mapas de flujo son los creados por Charles Joseph Minard (1781--1870), ingeniero francés pionero en su creación. Uno de esos mapas puede verse en la figura \ref{Fig:MapaFlujo}.

  $$\label{Fig:MapaFlujo}$$

• Cartogramas . En los cartogramas, la información cualitativa se transmite mediante la modificación de las unidades de superficie, que se distorsionan para representar con su tamaño la magnitud de la variable en cuestión. Es decir, la variable visual tamaño se aplica directamente sobre las distintas unidades de superficie. En la figura \ref{Fig:Cartograma} puede verse un ejemplo de cartograma en que los distintos estados de Estados Unidos se representan con un tamaño relativo a su número de votos electorales, evitando así que estados con poca densidad de población aparezcan en el mapa con una superficie y una preminencia que no les corresponde.

  $$\label{Fig:Cartograma}$$

Resumen

Hemos visto en este capítulo cómo un mapa constituye una forma de comunicación visual, y cómo en esa comunicación existen una serie de factores a tener en cuenta para que la transmisión de la información entre emisor y receptor sea óptima. De especial relevancia en este sentido es prestar atención a este último y tener siempre en cuenta el propósito del mapa que creamos.

Distinguimos dos tipos de cartografía: la cartografía de base y la temática. Esta última es la que crearemos con más frecuencia en un SIG. Las formas de cartografía temática están muy relacionadas con las características de la variable. Para el caso de variables cuantitativas, es importante agrupar adecuadamente los distintos valores en clases. Existen diversas formas de delimitar los intervalos correspondientes, siendo las más habituales el uso de intervalos iguales, intervalos naturales o intervalos basados en la media y la desviación típica de los valores en cuestión.

Dentro de los tipos de mapas temáticos más importantes encontramos los mapas de puntos, de símbolos proporcionales, de isolíneas y de coropletas, cada uno de ellos con sus características particulares. Los mapas de isolíneas son especialmente indicados para la representación de variables continuas, mientras que por su parte las variables de tipo razones se representan de forma especialmente adecuada mediante los mapas de puntos.

A la hora de componer un mapa existen diversos elementos que deben añadirse para facilitar su interpretación. Además de conocer la función de cada uno, es importante saber cómo situar estos sobre el lienzo del mapa, aprovechando correctamente el espacio e integrándolos adecuadamente.