Creación de capas vectoriales

Introducción

La conversión de datos espaciales desde el modelo vectorial al modelo ráster nos servía para obtener un dato espacial mucho más adecuado para el análisis. Para variables continuas tales como la elevación, los datos vectoriales resultan más difíciles de analizar, por lo que el tipo de conversión que vimos era un paso previo para poder acceder a toda la potencia de análisis de un SIG.

Las ventajas del modelo ráster, que fueron comentadas con detalle en el capítulo Tipos_datos , lo convierten en la opción preferida a la hora del análisis de variables continuas, pero esta no es, ni mucho menos, la única tarea que podemos realizar en un SIG. Para muchas de esas restantes tareas, el modelo vectorial es preferible, pues, como ya vimos, también tiene su particular serie de ventajas.

Si en el capítulo Creacion_capas_raster estudiábamos como convertir los datos vectoriales en datos ráster, debemos ver de igual forma cómo proceder en sentido inverso cuando esto sea posible, y mostrar qué formas vectoriales del dato espacial resulta posible obtener a partir de una capa ráster. El proceso que vamos a ver no es sencillamente el inverso de lo entonces presentado, sino que implica otra serie de operaciones.

Así, la conversión de puntos en una capa ráster, que nos ocupó la mayoría de paginas en aquel capítulo, no tiene un equivalente en la conversión de una capa ráster en una de puntos, pues esta segunda operación resulta obvia con los conocimientos que ya tenemos. Basta aplicar las ecuaciones vistas en Variables_algebra_mapas para calcular los valores de la variable en dichos puntos.

Otras operaciones, sin embargo, tales como convertir una capa ráster en una capa vectorial no de puntos sino de isolíneas, sí que requieren algo más de explicación. Más aún, resulta importante mostrar al lector que esos procesos existen y son parte de los procesos que un SIG nos ofrece, para que pueda incorporarlas a su batería de herramientas.

La coexistencia de los datos vectoriales y ráster no solo es una realidad, sino que en muchas ocasiones es una necesidad. A lo largo de las distintas fases de trabajo dentro de un proyecto SIG, un mismo dato puede emplearse de varias formas distintas con objeto de satisfacer las distintas necesidades que aparezcan. Como muestra la figura \ref{Fig:Conversiones}, para una capa de elevaciones, las conversiones entre modelos de datos aparecen en diversos puntos dentro de un ciclo de trabajo habitual. Una de ellas es una conversión de vectorial a ráster tal y como las que vimos en el capítulo anterior. Las restantes son en sentido inverso (de ráster a vectorial), como las que trataremos en el presente.

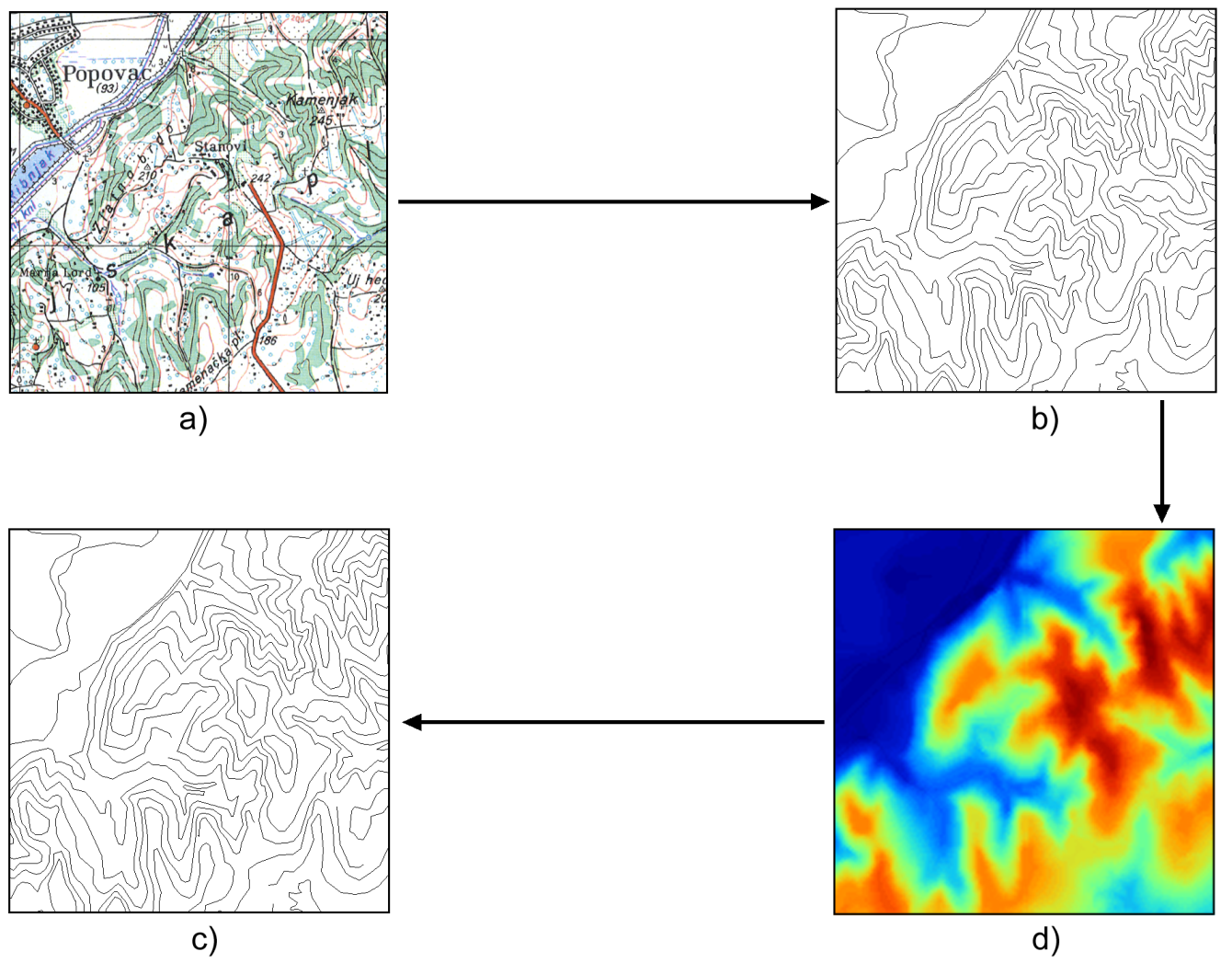
Distintas conversiones de modelo de datos, a lo largo de un proceso de trabajo con una capa de elevaciones: a) mapa escaneado, b) curvas de nivel, c) capa ráster, d) curvas de nivel.

En el esquema de la figura, partimos de un mapa escaneado, el cual es una imagen donde se pueden ver las curvas de nivel con sus valores de altitud correspondientes. Se trata de una capa ráster, pero los análisis que podemos realizar a partir de ella son prácticamente nulos. En realidad, no es más que un «dibujo». Para obtener un dato más susceptible de análisis debemos vectorizar esas curvas de nivel, convirtiéndolas en una capa vectorial de líneas. Este proceso de vectorización ya se comentó en el capítulo Fuentes_datos , cuando vimos las fuentes de datos más habituales.

Como se dijo entonces, esa digitalización puede llevarse a cabo manualmente, bien digitalizando en pantalla o bien con alguna otra herramienta más específica. Esa conversión no es, sin embargo, la que interesa a este capítulo, ya que aquí veremos los procesos y algoritmos que pueden automatizar esta tarea de reconocer las líneas de ese mapa escaneado y delinear en base a ellas las entidades de la capa vectorial resultante.

A partir de esa capa de líneas, el siguiente paso es la obtención de una capa ráster. Todo lo necesario para llevar a cabo este proceso ya lo hemos visto en el capítulo Creacion_capas_raster .

Por último, a partir de esa capa ráster podemos obtener de nuevo un dato vectorial tal como un TIN, o bien de nuevo unas curvas de nivel. En el caso de la figura, las curvas de nivel son anteriores a la capa ráster, con lo cual este paso no resulta de gran utilidad, pues ya disponemos de ellas. Sin embargo, sabemos que hay tecnologías que permiten obtener una capa de elevaciones ráster sin necesidad de partir de un dato vectorial, y en ese caso la obtención de este último implica necesariamente un cálculo a partir de la capa ráster. Las curvas de nivel pueden sernos útiles para, por ejemplo, generar un resultado cartográfico, y en este capítulo veremos en qué se basan las formulaciones que nos permiten hacer tal conversión.

A lo largo de este capítulo vamos a ver dos clases de procesos para crear capas vectoriales a partir de capas ráster.

Conversión de capas ráster discretas. Vectorización.
Conversión de capas ráster continuas.

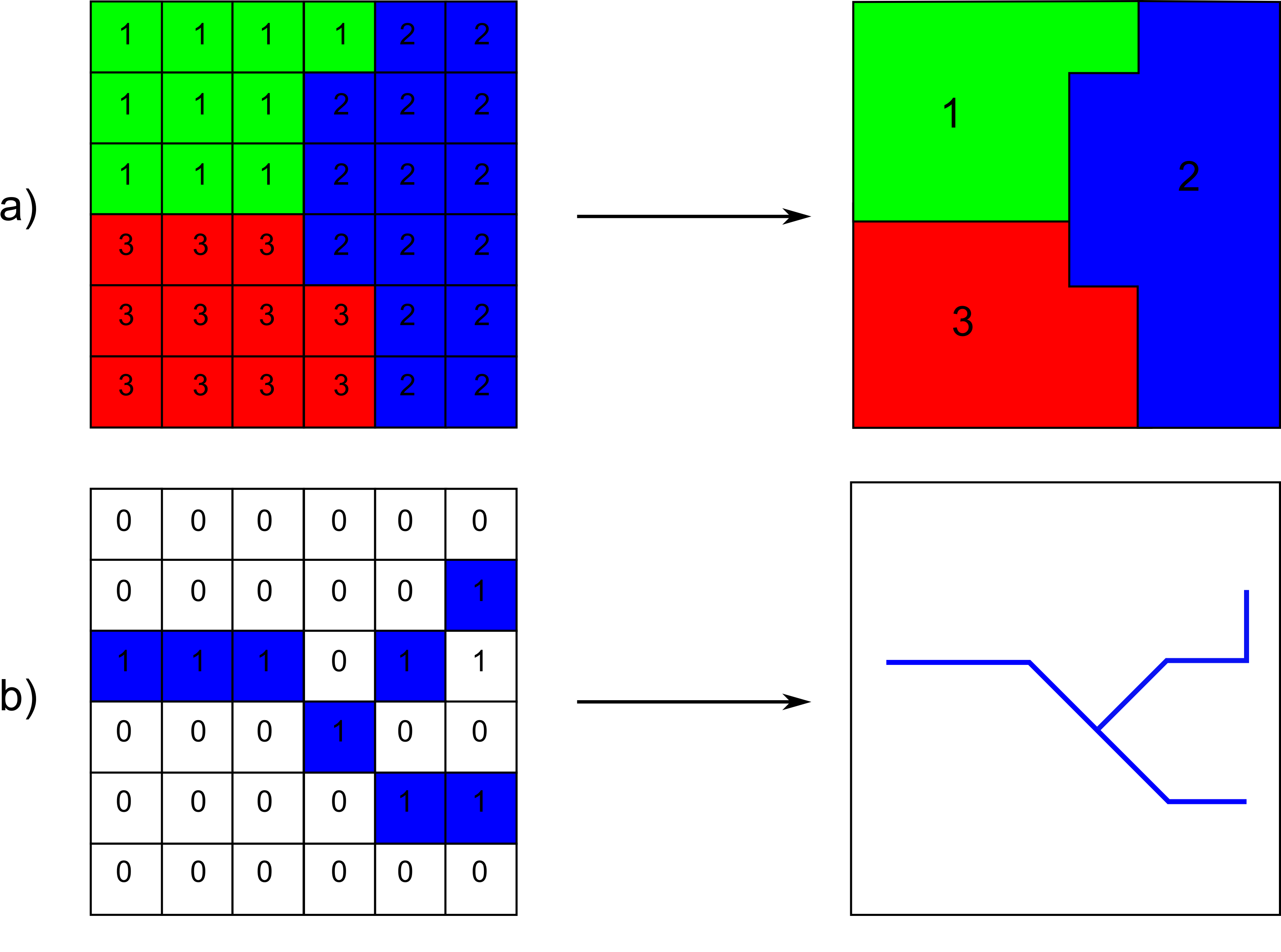
Partiendo de una capa ráster discreta, el proceso de vectorización pretende generar una capa vectorial que recoja las geometrías que aparecen en dicha capa. Estas geometrías vienen definidas por la forma en que los valores de las mismas clases se disponen en la malla de celdas. Este es el caso que encontramos cuando disponemos de una capa ráster pero el modelo conceptual del espacio geográfico no es el modelo de campos, sino un modelo de entidades discretas. Cada una de estas entidades se constituyen mediante conjuntos de celdas contiguas con el mismo valor. Esta idea se recoge en la figura \ref{Fig:Vectorizacion}

Vectorización de capas ráster discretas en capas de polígonos (a) y de líneas (b). .

En la conversión de capas continuas, veremos cómo expresar una capa ráster continua mediante un conjunto de entidades, en particular mediante líneas y polígonos. Para el caso de líneas, analizaremos cómo delinear un conjunto de isolíneas a partir de una capa ráster. En el caso de polígonos, estudiaremos cómo crear un TIN, estructura de triángulos irregulares que, como ya vimos, sirve para almacenar variables continuas, particularmente la elevación.

Vectorización de entidades

La vectorización de entidades tiene como base una capa ráster con una variable de tipo nominal u ordinal, en la cual se reflejan distintas categorías. El objetivo es expresar mediante entidades vectoriales los conjuntos de celdas de una misma categoría.

La necesidad de efectuar este tipo de operaciones va a aparecer habitualmente cuando encontremos en nuestro trabajo una capa ráster de este tipo, pues ya sabemos que resulta más adecuado en la mayoría de casos almacenar esta información según el modelo de datos vectorial.

Capas tales pueden surgir en el trabajo con SIG en diversos momentos, pues muchas operaciones de análisis sobre capas ráster van a generar este tipo de resultados. La conversión de dichos resultados al modelo de datos vectorial va a permitir darles un uso distinto y combinar ambos modelos de representación, utilizando cada cual cuando más convenga.

Estas operaciones pueden partir de capas ráster con variables continuas, de las que se extraen entidades de acuerdo a formulaciones diversas. Un ejemplo muy característico es la delineación de redes de drenaje y la delimitación de cuencas vertientes, operaciones ambas que se realizan a partir de un Modelo Digital de Elevaciones, como vimos en el capítulo Geomorfometria .

Otros procesos de vectorización que ya conocemos son los que se llevan a cabo a partir de cartografía escaneada. En este caso, no obstante, la situación es bien distinta, ya que lo que a simple vista parece una misma línea o un mismo polígono en el mapa escaneado, realmente no es un conjunto de celdas con un único valor (es decir de un único color), sino con varios valores (colores) similares. Esta situación hace más difícil trabajar con este tipo de capas a la hora de vectorizar y reconocer las entidades que se deben vectorizar, y requiere procesos previos de tratamiento para que ese mapa escaneado se encuentre en las mejores condiciones antes de proceder a la vectorización. La figura \ref{Fig:Condiciones_vectorizacion} muestra una imagen que contiene líneas y polígonos, y junto a ellas las representaciones de estas que resultan óptimas para proceder a vectorizarlas como capas de líneas o capas de polígonos respectivamente.

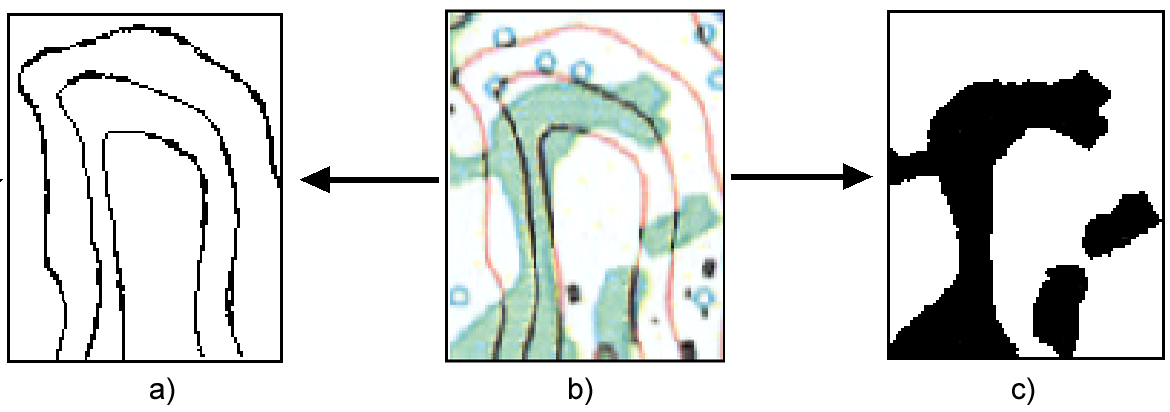
b)Imagen con polígonos y líneas para vectorizar. a) y c) La misma imagen tras ser trasformada con objeto de mejorar las condiciones para la vectorización (como capas de líneas y polígonos respectivamente) y aumentar la calidad de esta.

El paso de las versiones originales a estas versiones óptimas implica el uso de operaciones de álgebra de mapas, así como las que se vieron en las secciones Segmentacion o Operaciones_morfologicas , dentro del capítulo dedicado al tratamiento de imágenes. Los algoritmos que trataremos en esta sección supondrán ya que se trabaja sobre una capa donde las entidades a vectorizar están representadas por valores uniformes, dependiendo su rendimiento de esta circunstancia. Aun así, haremos mención también a los procesos de preparación previos, ya que en algunos casos son parte inseparable de ciertos procesos de vectorización muy frecuentes en un SIG.

Algoritmos para el tratamiento de imágenes no necesariamente en estas circunstancias óptimas se detallan en [ Price2006MsC ], donde pueden encontrarse algoritmos para vectorización de todo tipo de imágenes en color. Estos algoritmos están enfocados a un trabajo fuera del ámbito de los SIG, y por ello pueden no satisfacer exactamente las necesidades que se presentan dentro de nuestro campo.

Vectorización de líneas

Volviendo a los algoritmos sobre capas discretas donde las entidades a definir están claramente definidas, comencemos con los de vectorización de líneas. Estos son similares en cierta medida a los de polígonos que veremos más adelante, aunque entrañan en principio algo menos de dificultad técnica.

Una característica reseñable de los algoritmos de vectorización de líneas son sus mayores requerimientos en lo que respecta a las características de la capa de partida. Esto es así debido a que, a la hora de vectorizar una línea, vamos a necesitar que esta sea, en efecto, una línea como tal. Es decir, que el conjunto de celdas que la definen sea un conjunto de un único píxel de ancho, tal y como vimos en el apartado Esqueletizacion al tratar las operaciones de esqueletización.

Para el caso de polígonos, si en la obtención de una imagen binaria los polígonos han quedado más grandes o más pequeños, o con una forma u otra, este hecho no afecta al resultado. El algoritmo los reconocerá y los vectorizará, y su funcionamiento será igual en todos casos. Las imprecisiones que puedan existir en la imagen binaria se trasladarán a las capas vectoriales resultantes, pero los algoritmos de vectorización no verán afectado su funcionamiento por dichas imprecisiones.

En el caso de las líneas encontramos una situación bien distinta. La presencia de píxeles adicionales o la falta de conectividad entre líneas van a dificultar seriamente la vectorización, ya que los algoritmos correspondientes están pensados para trabajar sobre entidades lineales que cumplan las características citadas anteriormente.

En ocasiones, las capas con las que trabajamos van a estar en buenas condiciones de ser vectorizadas (por ejemplo, en el caso ya citado de una red de drenaje extraída a partir de un MDE). En otras muchas, sin embargo, las capas ráster con las que vamos a trabajar van a requerir procesos previos, habitualmente laboriosos. Por esta razón, la obtención de una capa óptima a vectorizar es el obstáculo principal que encontraremos, por ejemplo, cuando trabajemos con imágenes, ya que estas en la mayoría de los casos no cumplen las condiciones requeridas y hacen necesario un importante trabajo de preparación.

Para ver un ejemplo de lo anterior, trataremos una de las tareas que con más frecuencia se presenta dentro del trabajo con SIG: la digitalización de curvas de nivel de un mapa impreso. Automatizar la vectorización en sí no es en este caso una tarea altamente compleja, pero los procesos tales como la segmentación o las operaciones morfológicas que ya conocemos no resultan sencillos de ajustar de forma automática para obtener un resultado vectorizable. Es necesario en la mayoría de los casos un cierto grado de trabajo manual.

Debe pensarse que el mapa escaneado es habitualmente una imagen en color, más compleja que las imágenes binarias sobre las que se presentaron en el capítulo Procesado_imagenes las operaciones morfológicas. Por ello, resulta más difícil ajustar estos procesos.

El paso de una imagen original tal como el mapa escaneado de la figura \ref{Fig:Condiciones_vectorizacion} a uno más apto para la vectorización como el de la imagen $a)$ de dicha figura es un proceso más complejo de lo que puede parecer, ya que comporta las siguientes dificultades:

Las líneas tienen más de un píxel de ancho
Las líneas tienen píxeles de varios colores distintos
Aparecen elementos adicionales que dificultan la identificación automática de las líneas, pues rompen su continuidad. Por ejemplo, es habitual que las líneas se encuentren interrumpidas por etiquetas en las que se refleja su valor de elevación correspondiente. Otros elementos tales como ríos o carreteras pueden estar representados en el mismo mapa, y trazarse por encima de las curvas de nivel, que suelen quedar en un segundo plano. Mientras que estos últimos se trazan con colores diferentes a las curvas de nivel, las etiquetas tienen el problema añadido de que presentan el mismo color que la propia línea, con lo cual no pueden eliminarse en base a dicho color con procesos tales como la segmentación (véase el apartado Segmentacion ) [ Ananthanarayanan2006GISDev ].

El problema más grave de los anteriores es la falta de continuidad, el cual puede tratar de solucionarse tanto en la parte ráster, como en la vectorial, es decir, antes o después de la vectorización como tal. Para el ojo humano, resulta sencillo en caso de discontinuidad intuir cual es la conectividad de las lineas, ya que nuestra percepción tiende a agrupar aquellos elementos que sugieren una continuidad lineal, considerándolos como una entidad única pese a que en realidad no se encuentren unidos y sean objetos aislados. Por desgracia, un SIG no comparte con nosotros estas capacidades perceptivas, y es necesario que las uniones entre los tramos de líneas existan como tales de un modo más tangible.

Para el caso ráster, ya vimos en su momento (apartado Operaciones_morfologicas ) las operaciones morfológicas que nos pueden ayudar a «conectar» las líneas cuando hayan quedado separadas por alguna razón. Para el caso vectorial, existen de igual forma diversos algoritmos que tratan de realizar esta conexión una vez que la vectorización se ha producido y aparecen imprecisiones. En [ Pouderoux2007ICDAR ] puede encontrarse uno de tales algoritmos vectoriales, que no se detallarán aquí por estar fuera al alcance de este capítulo.

En líneas generales, y teniendo en cuenta los condicionantes anteriores, la vectorización de curvas de nivel a partir de mapas topográficos se lleva a cabo siguiendo una cadena de procesos que comporta los siguientes pasos.

Escaneado del mapa original
Filtrados y mejoras sobre la imagen resultante
Segmentación
Operaciones morfológicas
Conversión ráster--vectorial

siendo en este último paso en el que nos centramos dentro de este capítulo.

Para esta conversión ráster--vectorial, el algoritmo correspondiente debe seguir un esquema genérico como el siguiente, a aplicar para cada una de las curvas de nivel.

Localizar una celda de la curva.
Analizar las celdas alrededor suyo para localizar la siguiente celda de la curva.
Desplazarse a esa celda.
Repetir los pasos anteriores.

Este proceso se detiene hasta que se cumple un criterio dado, que es el que concluye la vectorización de la línea. En general, el criterio a aplicar suele ser que se regrese a la celda de partida, o que no pueda encontrarse una nueva celda entre las circundantes (a excepción de la anterior desde la cual se ha llegado a esta).

Siguiendo este esquema, se dota de un orden a las celdas de la línea. Mediante esta secuencia ordenada de celdas, puede crearse la línea vectorial como una secuencia ordenada de coordenadas (particularmente, las coordenadas de los centros de esas celdas).

Hay muchos algoritmos distintos de vectorización. Las diferencias van desde la forma en que se analizan las celdas circundantes o el criterio que hace que se concluya la vectorización de la línea, hasta formulaciones más complejas que siguen un esquema distinto.

Más allá de lo visto en este apartado, la conversión de mapas topográficos en capas de curvas de nivel es un proceso complejo del que existe abundante literatura. Buenas visiones generales de este pueden encontrarse en [ Arrighi1999Geovision ][ Chen2006IEEE ][ Leberl1982PERS ][ Greenlee1987PERS ]

Además de la vectorización de curvas de nivel, tarea habitual que ya hemos visto, existen otras muy variadas que presentan cada una de ellas distintas circunstancias. Así, y aún disponiendo ya de una capa que presente las condiciones idóneas para ser vectorizada, el proceso puede presentar más dificultad de la que con lo visto hasta este punto puede pensarse. No hay que olvidar que, a la hora de vectorizar un conjunto de líneas, estas se definen no únicamente por su forma, sino por otros elementos tales como, por ejemplo, la topología.

En el caso particular de vectorizar un conjunto de curvas de nivel tal y como lo venimos detallando, esta topología es clara y no entraña dificultad añadida a la hora de vectorizar. Por propia definición, las curvas de nivel no pueden cruzarse con otras curvas, con lo cual basta seguir el contorno de las mismas y no preocuparse de estos cruces. Sin embargo, vectorizar otros elementos implica tener en cuenta circunstancias distintas.

Algo más complejo que vectorizar curvas de nivel es hacerlo, por ejemplo, con una red de drenaje (recordemos que en el capítulo Geomorfometria vimos cómo extraer esta en formato ráster a partir de un MDT). En este caso sí que existen intersecciones, pero, puesto que los cauces solo tienen un único sentido, las formas que el conjunto de estos puede adquirir están limitadas. En particular, una red de drenaje es siempre una estructura en árbol, lo cual quiere decir que no van a existir rutas cíclicas en dicha red.

Si lo que tratamos de vectorizar es una red viaria, las posibilidades son más amplias, y además, como ya sabemos, el modelo ráster no es adecuado para registrar completamente la topología de dicha red. La existencia de rutas cíclicas complica además los algoritmos de vectorización en caso de que estos pretendan añadir topología a sus resultados, con lo que la operación no resulta tan sencilla como en el caso de las curvas de nivel.

En resumen, la existencia de topología añade complejidad a la vectorización de líneas. Aún así, siempre resulta posible (y en muchos casos suficiente) vectorizar estas y obtener como resultado una capa sin topología ( spaguetti ). Esta capa, ya en el modelo vectorial, puede tratarse posteriormente para dotarla de la topología necesaria, en caso de que así se requiera.

Vectorización de polígonos

Muy relacionada con la vectorización de líneas, tenemos como herramienta habitual dentro de un SIG la vectorización de polígonos. Esta guarda gran similitud con la anterior, en cuanto que el proceso se basa también, fundamentalmente, en ir siguiendo una serie de puntos y conectarlos, para de este modo definir el contorno del polígono.

Los puntos que nos interesan para la delineación de un polígono no son, a diferencia del caso de líneas, todos los que conforman el objeto a vectorizar, sino tan solo una parte de ellos. En concreto, van a resultar de interés únicamente las celdas exteriores, es decir, las que al menos tienen una celda circundante con un valor distinto al del propio polígono a vectorizar (en el caso de trabajar con una imagen binaria, las que tienen al menos una celda circundante que pertenece al fondo). Las celdas internas no nos aportan información relevante, ya en ellas no se va a situar ninguna de las coordenadas de la entidad vectorial que buscamos.

Siendo dichas celdas externas las que debemos tratar para delinear la entidad vectorial, el primer paso es, por tanto, su localización. Esta no es difícil si recordamos algunas de las operaciones morfológicas que vimos en el capítulo Procesado_imagenes . Por supuesto, la aplicación de estas exige que se den, una vez más, una buenas condiciones en la imagen, en particular que la frontera del polígono a vectorizar esté claramente definida. Para ello basta, como ya hemos dicho, que el valor dentro del polígono sea uniforme (valor que consideraremos como si fuera el 255 o 1 de las imágenes binarias, según lo comentado en su momento), y distinto de los restantes a su alrededor (valores todos ellos que consideraremos como el valor 0 de las imágenes binarias, que entonces identificábamos con el fondo)

a) Imagen base con un polígono a vectorizar. Las celdas que forman el contorno se muestran en gris. b) La imagen anterior tras un proceso de dilatación. c) Contorno del polígono obtenido a partir de la diferencia entre las dos imágenes anteriores.

De las operaciones morfológicas que conocemos, la erosión nos da una idea de la forma de proceder a la hora de localizar las celdas importantes. De la forma en que lo presentamos entonces, el proceso de erosión elimina aquellas celdas que se sitúan en contacto con el fondo y están en el borde del objeto. Estas son exactamente las que nos interesan de cara a la vectorización. Como muestra la figura \ref{Fig:Erosion_para_vectorizacion}, la diferencia entre una imagen binaria y dicha imagen tras un proceso de erosión es el contorno del objeto.

El proceso de erosión se aplica en este caso con un elemento estructural como el siguiente, en lugar del que vimos en el apartado Operaciones_morfologicas .

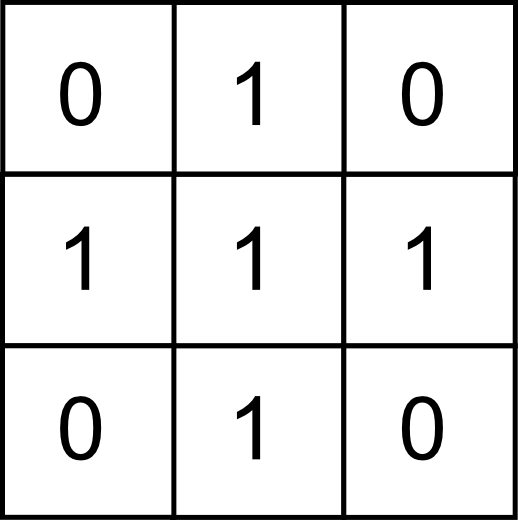
Esto no es estrictamente necesario ya que, de aplicar el que vimos entonces, y aunque el contorno resultante sería distinto, el resultado sería igualmente vectorizable el contorno resultante puede ser recorrido haciendo movimientos de torre, mientras que con el que hemos aplicado en este caso (y como puede apreciarse en la figura) recorrer el contorno exige movimientos en diagonal.\\ En la jerga del tratamiento de imágenes se dice que existe conectividad-4 en el primer caso y conectividad-8 en el segundo, haciendo referencia al numero de celdas circundantes a las que uno puede desplazarse según cada uno de estos esquemas de movimiento\\Otra forma habitual de referirse a estos conceptos es hablar de vecindad de Von Neumann para el caso de 4 posibles conexiones o vecindad de Moore para el caso de 8.}.

Sobre este contorno, el proceso de digitalización ya no difiere, a primera vista, del que efectuábamos sobre una curva de nivel. El objetivo es asignar un orden a las celdas de ese contorno, de modo que siguiendo dicho orden quede definido el perímetro del polígono.

Para ello, y como en el caso de las curvas de nivel, basta comenzar en uno de los puntos e ir siguiendo de un modo sistemático el contorno, añadiendo las coordenadas de los puntos recorridos. Dichas coordenadas, no obstante, no son en este caso las de los centros de las celdas, sino que se deben tomar las de los vértices para que esta forma se almacene el contorno de cada una de las celdas externas al objeto vectorizado. Particularmente, son de interés las coordenadas de aquellos vértices que se sitúan en el lado exterior del contorno. Esto puede comprenderse mejor viendo la figura \ref{Fig:Vertices_vectorizacion}.

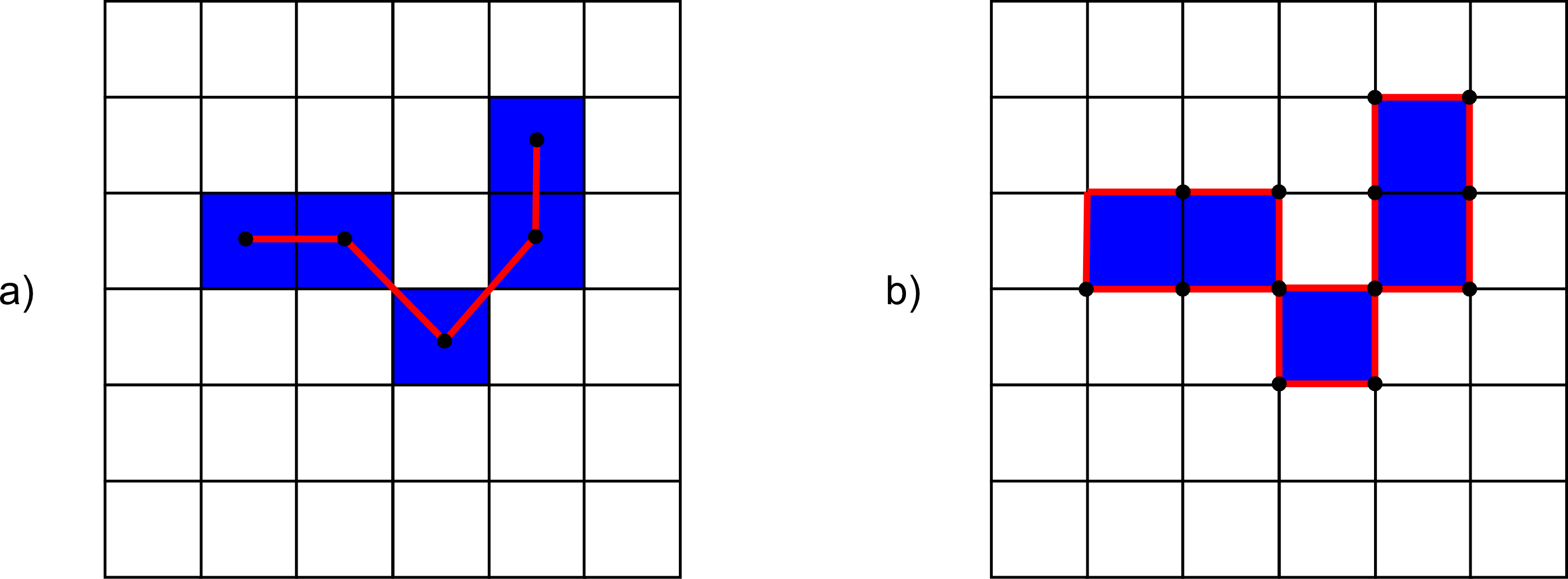
Mientras que en la vectorización de líneas (a) se toman las coordenadas del centro de la celda, en el caso de polígonos (b) se deben utilizar las de los vértices para delinear completo el contorno del objeto.

Los resultados en los dos supuestos representados en la figura son bien distintos, a pesar de que el objeto a vectorizar es el mismo, pero en un caso se interpreta como una línea y en otro como un polígono.

Un algoritmo para vectorizar el contorno de un polígono debe localizar una celda de dicho contorno e ir avanzando hasta rodear por completo este, almacenando las coordenadas de los bordes exteriores de todas las celdas recorridas. El avance se detiene cuando se vuelve a la misma celda en la que se comenzó, momento en el cual el proceso de vectorización queda completo. En [ Pavlidis1982CSP ] puede encontrarse con más detalle la descripción de un algoritmo de esta forma, parte de cuyos fundamentos pueden emplearse igualmente para la vectorización de líneas.

Al igual que sucedía con dichas líneas, la complejidad del objeto puede presentar problemas para su vectorización. El algoritmo anterior no contempla, por ejemplo, la presencia de «huecos» en el polígono. Como ya conocemos, esos huecos son polígonos internos que han de incorporarse a su vez a la entidad, y por tanto deben ser a su vez vectorizados.

Isolíneas

Otro resultado vectorial que puede generarse a partir de una capa ráster son las isolíneas o curvas de nivel. Aunque el caso más habitual es utilizarlas para representar elevaciones (tal y como aparecen en un mapa topográfico habitual), se emplean también para otro tipo de variables de tipo continuo tales como la presión ( isobaras ), la precipitación( isoyetas ) o el tiempo( isocronas ). La forma de obtenerlas a partir de una capa ráster es, no obstante, la misma en todos los casos.

En un apartado anterior, veíamos cómo vectorizar un mapa escaneado que contiene el trazado de dichas curvas de nivel. En este, veremos cómo hacerlo cuando disponemos de los datos de elevación como tales en lugar de unas curvas ya trazadas en una imagen. Mientras que en aquel caso obteníamos curvas de nivel con la equidistancia utilizada en el mapa escaneado (es decir, el trabajo de traza las curvas ya estaba hecho y el proceso no hacía sino convertirlas en entidades vectoriales), aquí podemos definir nosotros esa equidistancia y los valores para los que queremos obtener tales curvas.

El calculo de curvas de nivel puede realizarse a partir de una capa ráster, pero también a partir de una capa de puntos con datos de elevación. En este ultimo caso, no obstante, ya sabemos que podemos convertir esos puntos en una capa ráster mediante métodos de interpolación (según lo visto en el capítulo Creacion_capas_raster ), y después en base a este calcular las curvas de nivel. En esta sección trataremos únicamente la delineación de curvas de nivel a partir de capas ráster.

Un método basado en triangulación para obtener curvas de nivel a partir de puntos distribuidos irregularmente se detalla en [ Brunet1984Questiio ]. Una revisión detallada de métodos disponibles para esta tarea se puede encontrar en [ Sabin1980Academic ].

Respecto al cálculo a partir de una estructura regular como una capa ráster, los algoritmos correspondientes no derivan únicamente del trabajo con SIG, sino que se trata de un área muy desarrollada en el tratamiento de imágenes digitales. Las curvas de nivel ponen de manifiesto las transiciones existentes en los valores de la imagen, y estos puede resultar de interés para una mejor interpretación de esta o la automatización de ciertas tareas.

Existen dos enfoques principales a la hora de trazar curvas de nivel en base a una malla de datos regulares [ Sutcliffe1980Academic ]

Seguimiento de líneas
Análisis por celdas

En el seguimiento de líneas, se localiza un punto que pertenezca a la curva de nivel y después se «sigue» esa curva de nivel hasta que se alcanza un borde de la malla ráster, o bien la curva se cierra regresando al punto inicial.

La localización de un punto de la curva se hace empleando métodos de interpolación, del mismo modo que veíamos en la sección Variables_algebra_mapas al tratar las técnicas de remuestreo. Como es lógico pensar, los valores de las curvas de nivel que se van a trazar son en generales valores «redondos» (múltiplos de 100 o 200, por ejemplo). Por el contrario, los valores de las celdas pueden ser cualesquiera, y salvo en casos particulares, los valores de las curvas de nivel no van a presentarse en los valores exactos de las celdas, que por convenio corresponden como sabemos a los centros de estas.

Dicho de otro modo, las curvas de nivel no pasan por los centros de las celdas, pero sí que atraviesan estas. Los métodos de interpolación se emplean para saber por dónde atraviesa exactamente la celda la curva de nivel correspondiente, ya que con los valores de una celda y sus circundantes, referidos a sus respectivos centros, pueden estimarse valores en puntos no centrales de estas.

Cuando una curva de nivel entra en una celda, obligatoriamente debe salir de ella (una curva de nivel, por definición, no puede concluir bruscamente salvo que se encuentre en el extremo de la malla de celdas). Los mismos métodos de interpolación se emplean para calcular por dónde sale y hacia qué celda lo hace. Sobre esa celda se aplicará un análisis similar, y de este modo se produce ese seguimiento de la línea que resulta en el trazado completo de la curva de nivel.

El resultado de este proceso es un conjunto de puntos que unidos secuencialmente conforman la curva de nivel buscada.

Estos métodos tienen la ventaja de que, al presentar la línea como un continuo, dan resultados mejores para su representación (esto era especialmente importante cuando se empleaban plotters para la impresión de esos resultados), y es más fácil etiquetar el conjunto de líneas [ Snyder1978ACM ]. Esto es así debido a que los métodos que realizan un análisis por celdas no tratan la curva de nivel como una única entidad, sino como un conjunto de pequeños tramos, cada uno de los cuales definido en el interior de una única celda.

Aunque el resultado visualmente puede ser el mismo, la capa generada mediante un método de seguimiento de curvas va a contener menos entidades y ser más correcta desde un punto de vista semántico, ya que una curva se expresa como una única entidad, no como un conjunto de ellas.

Entre los métodos de análisis por celdas, uno con gran relevancia (especialmente en el tratamiento digital de imágenes) es el conocido como Marching Squares , una adaptación bidimensional del algoritmo tridimensional Marching Cubes presentado en [ Lorensen1987SIGGRAPH ].

El fundamento de este método es el hecho de que, si una curva de nivel atraviesa una celda, existen únicamente 16 posibles configuraciones de los vértices de esa celda en función de si su valores correspondientes están dentro o fuera de la curva de nivel. La figura \ref{Fig:Marching_squares} muestra esas configuraciones.

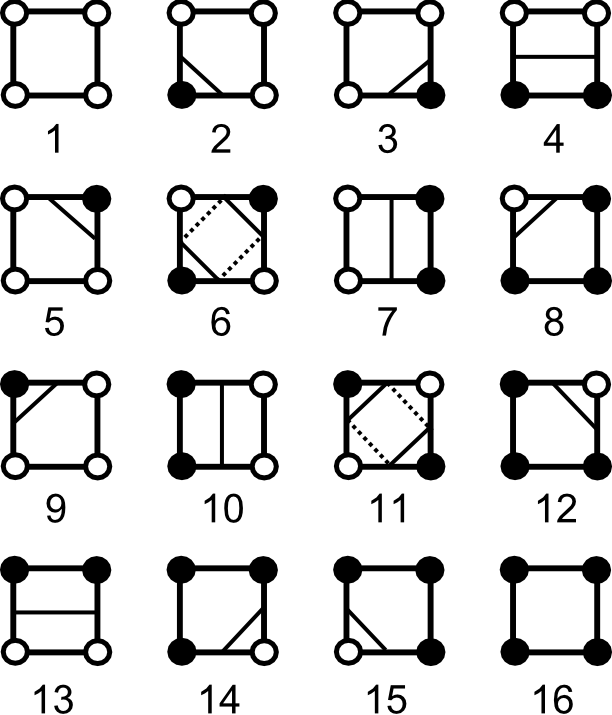
Posibles configuraciones de una celda según el algoritmo *Marching Squares* . Los vértices en negro estan dentro de la curva de nivel, mientras que los blancos se encuentran fuera.

En base a esto, se recorren todas las celdas, se analiza en cuál de las configuraciones se encuentra cada una de ellas y, cuando corresponda, se traza una línea entre el punto de entrada y de salida de la curva de nivel en la celda. Estos puntos se calculan, al igual que ya veíamos para los métodos de seguimiento, mediante interpolación.

El algoritmo no establece relación alguna entre las celdas por las que pasa una misma curva de nivel, sino que toma estas separadamente. Por ello, aunque visualmente los tramos que resultan estén conectados, son considerados como segmentos independientes a la hora de generarlos, y también a la hora de su manejo una vez la capa de curvas de nivel ha sido creada.

Además de este inconveniente, el método presenta algunas ambigüedades, como puede verse en la figura \ref{Fig:Marching_squares} para los casos 6 y 11. En estos supuestos no está clara cuál es la forma en que la curva de nivel atraviesa la celda. En los métodos de seguimiento no existe esta deficiencia, ya que se sabe desde qué celda llega la curva de nivel.

Creación de TIN

Ya conocemos los TIN como estructuras vectoriales utilizadas para almacenar una variable continua tal como la elevación. Como vimos en el capítulo Tipos_datos , estos están formados por un conjunto de puntos que, utilizados como vértices de triángulos, dan lugar a una red de triángulos interconectados que cubren toda la superficie estudiada.

Estos triángulos aparecen en mayor número en las zonas donde la variable presente una mayor variabilidad (relieve más abrupto) y en menor número cuando no existe una variabilidad tan acusada (relieve llano).

La creación de un TIN a partir de otro modelo de datos como, por ejemplo, una capa ráster, implica las siguientes operaciones:

Selección de puntos más representativos.
Triangulación de dichos puntos.

Selección de puntos

No todas las celdas de la capa ráster son igual de interesantes a efectos de crear un TIN. Si tomásemos todas las celdas y las utilizáramos como vértices, el TIN resultante sería sin duda preciso, pero el número de triángulos sería muy elevado. No estaríamos aprovechando la gran ventaja de los TIN, que no es otra que su adaptabilidad en función de la variabilidad de cada zona, ya que no estaríamos teniendo en cuenta esta variabilidad para tomar más o menos puntos según sea necesario.

Si se debe tomar un número de puntos menor, es necesario un método para eliminar aquellos que aportan menos valor al TIN resultante, de forma que, con los puntos que se consideren, este sea lo más preciso posible.

La significancia de una celda es la media de las significancias según las cuatro direcciones definidas. Para una dirección definida (en rojo), la significancia es la distancia $d$ entre la celda central y la recta que une las celdas de los extremos

La selección de las celdas que deben considerarse como vértices de la red puede llevarse a cabo mediante diversos algoritmos. El algoritmo conocido como VIP( Very Important Points )[ Chen1987Autocarto ] es uno de los más habituales. Se basa en evaluar la significancia de cada celda y después eliminar aquellas menos relevantes hasta quedarse con un número $n$ de celdas, que serán las más adecuadas para formar el TIN. El criterio de eliminación de celdas menos significativas puede también basarse en un umbral de significancia, de forma que solo se consideren como vértices las celdas que lo superen.

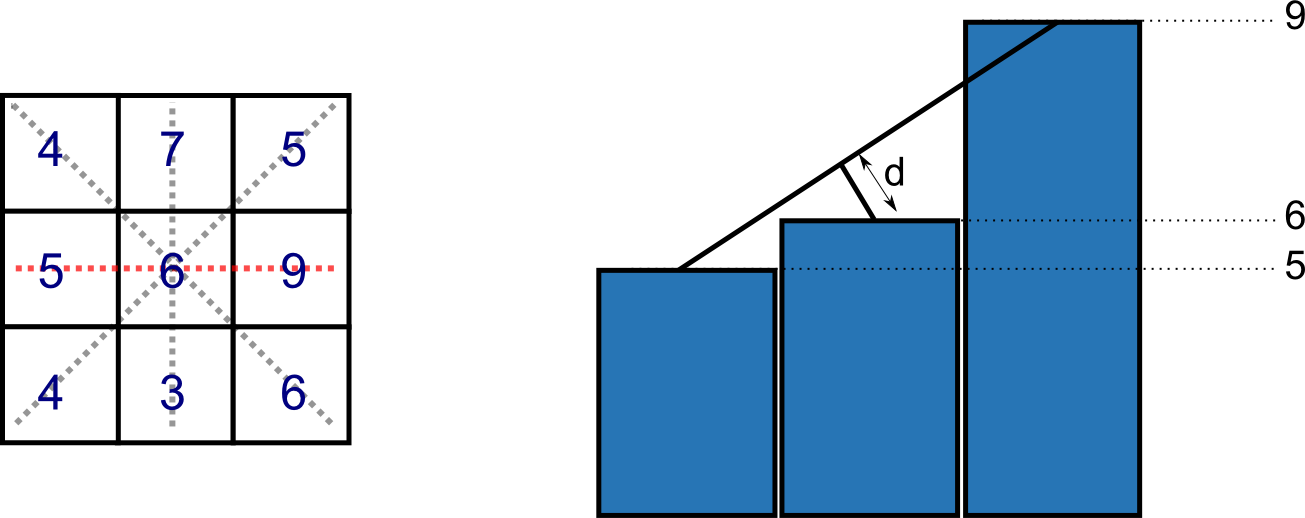
La significancia de una celda se obtiene mediante un análisis local con una ventana $3\times 3$, estudiando las cuatro posibles direcciones que pasan por la celda central (Figura \ref{Fig:Significancia_TIN}).

En cada dirección se traza una recta que pasa por dos puntos extremos, teniendo en cuenta la elevación de los mismos. La distancia entre la celda central y dicha recta es la que define la significancia. La media de las cuatro significancias calculadas según todas las direcciones posible es la significancia global de la celda.

Otro algoritmo basado en análisis local es el propuesto por [ Fowler1979CG ], que se basa en el análisis de las formas del terreno mediante ventanas $3\times 3$ y $2\times 2$, y busca hallar los puntos más representativos mediante la caracterización del tipo de forma del terreno. El análisis mediante la ventana $2\times 2$ es muy similar a lo que vimos en el análisis hidrológico para la localización de celdas cóncavas, en el capítulo Geomorfometria .

Un enfoque distinto a los anteriores es el propuesto por [ Lee89ACSM ], denominado drop heuristic , que crea un TIN con todas las celdas y después recorre iterativamente todos sus vértices, eliminando aquellos que se evalúen como de menor importancia.

Triangulación

Una vez que se tiene el conjunto de puntos significativos, es necesario conectar estos para formar la red de triángulos como tal, existiendo para ello existen diversas metodologías.

Para un conjunto de puntos $V$, una triangulación es una conjunto de triángulos que cumple las siguientes propiedades[ Dyn1990IMA ]:

El conjunto de todos los vértices de esos triángulos es igual a $V$.
Cada lado de un triángulo contiene únicamente dos vértices.
La intersección de dos triángulos cualesquiera es nula.
La unión de todos los triángulos forma la envolvente mínima convexa del conjunto de puntos.}.}

Los algoritmos de triangulación de un conjunto de puntos se basan la mayoría en considerar la tarea como un problema de optimización, siendo diversos los criterios aplicados. No obstante, es interesante que las propiedades de la triangulación guarden relación con el uso que vamos a darle al considerarla el elemento definitorio de un TIN, siendo esta una estructura en la que recogemos en general la forma de un terreno.

Puesto que dentro del triángulo van a asumirse unas propiedades constantes (pendiente, orientación), la idea es que los triángulos engloben áreas que, efectivamente, sean constantes en este aspecto. Esto se logra favoreciendo la creación de triángulos con ángulos cercanos a 60°, de modo que dichos triángulos sean lo más homogéneos posibles, evitándose aquellos de formas alargadas.

La forma más habitual de lograr esto es creando un tipo particular de triangulación conocida como Triangulación de Delaunay [ Delaunay1934OMEN ]. Esta presenta las siguientes propiedades:

Dado un triángulo cualquiera de dicha triangulación, el círculo que en que se inscribe no contiene a ningún otro punto.
Dados cuatro puntos que forman dos triángulos contiguos, la triangulación maximiza el mínimo ángulo interno del cuadrilatero formado.

Esta ultima propiedad es de especial interés para garantizar que los triángulos son óptimos en cuanto a su capacidad de representar fielmente el relieve.

La triangulación de Delaunay es el dual de otra estructura denominada Teselación de Voronoi , como puede verse en la figura \ref{Fig:Delaunay_Voronoi}. La teselación de Voronoi asocia a cada punto un polígono que representa el lugar geométrico de las coordenadas que tienen a dicho punto como punto más cercano de todos los del conjunto. Esto es similar a lo que veíamos para el método de interpolación por vecino más cercano, el cual genera, de hecho, una teselación de Voronoi.

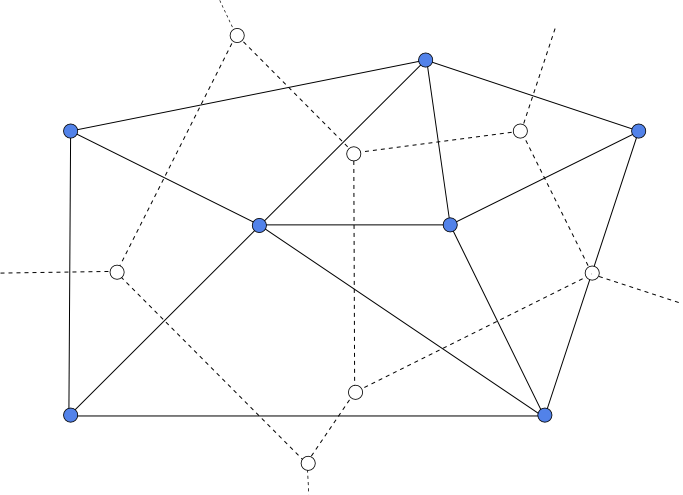
Teselación de Voronoi (en trazo discontinuo) y Triangulación de Delaunay (en trazo continuo) a partir de un conjunto de puntos (en azul)

Los algoritmos para crear una triangulación de Delaunay son abundantes, y existe mucha literatura al respecto. Comparaciones entre los más habituales y descripciones de estos pueden encontrarse en [ Su1995ACM ] y [ Fortune1992WC ], donde se tratan con detalle los más importantes.

Aunque este tipo de triangulaciones son las más recomendables, la propia naturaleza de un TIN puede aprovecharse para crear otras triangulaciones derivadas que, aun no cumpliendo las condiciones de la triangulación de Delaunay, representan de forma más fiel el relieve. La incorporación de las denominadas líneas de ruptura o líneas de falla es una de las modificaciones de mayor interés.

Dentro de un triángulo se asume que la pendiente y la orientación son constantes, y dicho triángulo define un plano en el espacio. Al pasar de un triángulo a otro, el cambio se produce justo en el lado que comparten dichos triángulos, representando dicho lado una línea de cambio. Si estas líneas de cambio coinciden con las líneas naturales en las que el relieve real que se quiere modelizar sufre un cambio brusco, el modelo obtenido será más fiel a la realidad.

En base a esta idea, puede forzarse a que dichas fallas naturales coincidan con los lados de los triángulos, definiéndolas explícitamente junto a los puntos que van a formar la base de la triangulación. La triangulación resultante no es de Delaunay, pero es más cercana a la verdadera forma del terreno, ya que incorpora información adicional.

Simplificación

Además de los métodos anteriores para seleccionar un conjunto reducido de puntos significativos y los algoritmos para obtener una red de triángulos a partir de estos, otro procedimiento importante es la simplificación de una red ya creada.

Como se muestra en la figura \ref{Fig:Simplificacion_triangulacion}, pueden eliminarse puntos de una triangulación y rehacer esta con los puntos restantes. Este es el fundamento del proceso de simplificación, eliminando progresivamente vértices y, cada vez que uno de ellos es eliminado, recalculando la triangulación de la mejor forma posible.

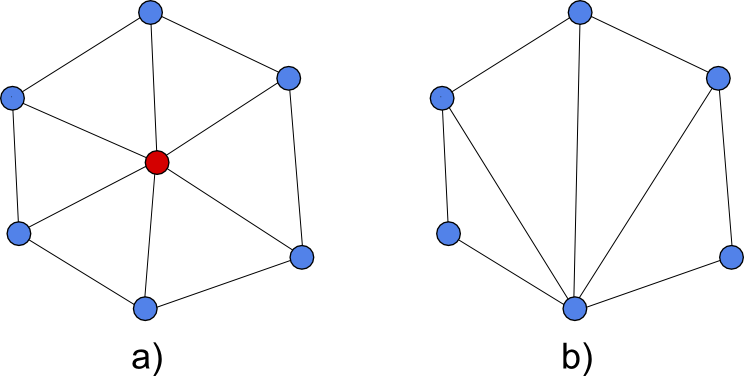
Esquema de la eliminación de un vértice (en rojo) en una triangulación

Este procedimiento de simplificación es similar al que vimos para el algoritmo de selección de puntos drop heuristic , que partía de un TIN muy denso con todas las celdas ráster como vértices. Si en lugar de partir de dicho TIN se comienza con otro calculado según algún otro algoritmo, este puede irse simplificando hasta alcanzar un nuevo nivel de precisión fijado de antemano. La figura \ref{Fig:TIN_Simplificado} muestra un TIN y dos versiones simplificadas del mismo, de distinto grado de simplificación. Nótese cómo en la imagen, si se eliminan puntos del exterior, varía el contorno de la triangulación.

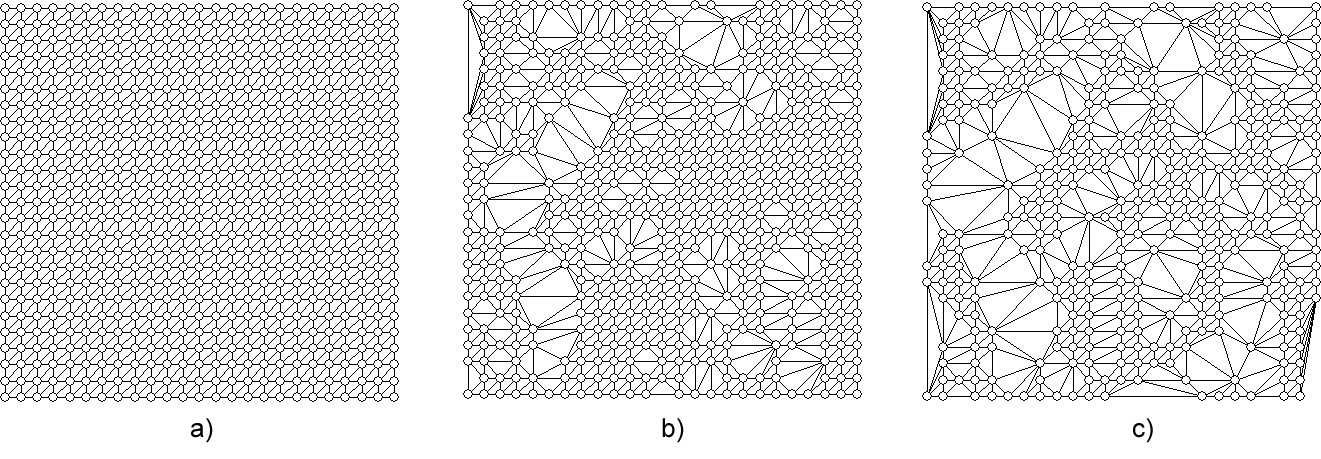
TIN original (a) y dos simplificaciones (b, c) en base al anterior.

Más detalle sobre algoritmos de simplificación puede encontrarse en [ andrews96simplifying ].

Resumen

Las capas ráster pueden convertirse en capas vectoriales empleando algoritmos a tal efecto. Estos algoritmos pueden aplicarse sobre capas ráster de variables continuas o discretas, siendo distintos en cada caso. En el caso de variables discretas, las capas vectoriales generadas definen las geometrías que forman las distintas clases dentro de la capa ráster. Estas geometrías pueden ser poligonales o lineales.

En el caso de variables continuas, las capas vectoriales que se generan pueden ser de los tres tipos básicos de geometrías: puntos, líneas o polígonos. Para generar una capa de puntos, la conversión no requiere ningún algoritmo específico, pues basta calcular los valores de la capa ráster en las coordenadas de dichos puntos. Para representar una variable continua mediante líneas, se crea una capa de isolíneas. Por último, para el caso de polígonos, una estructura como un TIN puede generarse igualmente a partir de la capa ráster, seleccionando los puntos más importantes y después triangulándolos.