Fundamentos cartográficos y geodésicos

Introducción

La característica principal de la información georreferenciada es que tiene una localización en el espacio, particularmente en el espacio terrestre. Esta localización se ha de dar por medio de unas coordenadas que la definan de forma adecuada, lo cual implica la necesidad de establecer un sistema en base al cual expresar dichas coordenadas.

Si medimos un dato de temperatura necesitamos un sistema de medición conocido, sin el cual el dato de temperatura en sí carece de valor y significado. Así, no es lo mismo decir que una temperatura es de 25 grados Celsius o que es de 25 grados Fahrenheit. Del mismo modo, si a esa temperatura le queremos asociar algún tipo de información espacial (por ejemplo, el punto exacto en el que fue medida), debemos establecer un sistema que permita dar sentido a las mediciones que realicemos, y que posteriormente nos sirva para interpretar los valores de las coordenadas y poder saber con exactitud dónde está el punto al que estas hacen referencia.

El establecimiento de un sistema de referencia en el que expresar la situación de un punto dado no es en absoluto una tarea sencilla, y requiere el conocimiento de abundantes conceptos previos que van desde ideas físicas hasta complejos desarrollos matemáticos y geométricos. Los avances en este campo han sido constantes desde la antigüedad, y esta evolución es la que ha permitido que en la actualidad se puedan obtener resultados altamente precisos en el trabajo con información georreferenciada. Gran parte de lo que podemos hacer en un SIG carecería de sentido si no se dispusiera de metodologías bien desarrolladas para el establecimiento de sistemas de referencia.

La geodesia es la ciencia encargada de proveer el marco teórico en el que fundamentar todo lo anterior, y es una disciplina compleja con diversas ramas de estudio. Todas ellas responden al objetivo básico de estudiar la forma de la Tierra, ya que debemos saber cómo es la Tierra para poder localizar puntos sobre su superficie. La determinación de la forma y dimensiones de la Tierra es tarea de la denominada geodesia esferoidal , cuyo cometido coincide con el del concepto clásico de geodesia, esto es, la definición de la figura terrestre. No obstante, en la actualidad encontramos otras ramas como la geodesia física , encargada de analizar el campo gravitatorio terrestre y sus variaciones, o la astronomía geodésica , que utiliza métodos astronómicos para la determinación de ciertos elementos geodésicos muy importantes que veremos más adelante. En conjunto, todas estas ramas dan forma a una serie de métodos y conceptos que son los que van a permitir la utilización rigurosa de coordenadas.

La necesidad del estudio geodésico surge por el hecho de que la Tierra no es plana, y cuando el territorio que pretendemos estudiar es lo suficientemente extenso, la curvatura de la Tierra no puede ignorarse. Este es el caso que vamos a encontrar cuando trabajemos con un SIG, y es por ello que los SIG implementan los elementos necesarios para poder efectuar un manejo de la información geográfica riguroso y acorde con los conceptos de la geodesia.

Vimos en el primer capítulo de esta parte que existen otras aplicaciones que trabajan con información georreferenciada, entre las cuales estaban los programas de diseño asistido por ordenador (CAD). Decíamos entonces que una de las principales limitaciones de estos era su mala disposición al trabajo con zonas extensas, ya que han sido diseñados para operar con zonas de unas dimensiones reducidas.

Cuando un arquitecto diseña el plano de una casa con una aplicación CAD, no necesita emplear los conceptos de la geodesia, puesto que a esa escala la forma de la Tierra no tiene relevancia. Aun prescindiendo de ella, puede expresar las coordenadas de los distintos elementos (un muro, un pilar, etc.) con la suficiente precisión y corrección como para que luego pueda construirse esa casa. Sin embargo, cuando un usuario de SIG estudia la cuenca vertiente de un río o la distribución de población en las regiones de un país, o bien analiza las rutas migratorias de un ave entre dos continentes, los conceptos de la geodesia resultan fundamentales.

En la actualidad, los SIG han hecho que la información geográfica tenga en muchos casos carácter global y cubra grandes extensiones o incluso la totalidad del planeta. Esto obliga más que nunca a hacer hincapié en los fundamentos geodésicos que resultan básicos para que toda esa información pueda manejarse correctamente, siendo de interés para cualquier usuario de SIG, con independencia de su escala de trabajo.

Otro aspecto básico a la hora de trabajar en un SIG son las denominadas proyecciones cartográficas . Estas permiten transformar las coordenadas sobre la superficie curva de la Tierra en coordenadas sobre una superficie plana. Esto es necesario para poder representarlas en un soporte plano tal como puede ser un mapa o la pantalla del ordenador, así como para poder analizarlas de forma más simple.

Con los elementos de la geodesia y las proyecciones cartográficas ya podemos elaborar cartografía y estamos en condiciones de trabajar con la información georreferenciada. No obstante, existen ciertos conceptos relativos a esa cartografía que resultan de suma importancia y deben conocerse antes de abordar esas tareas. El más importante de ellos es la escala, es decir, la relación entre el tamaño real de aquello que representamos y su tamaño en la representación, la cual constituye un factor básico de toda información cartográfica.

La escala condiciona a su vez la aparición de otra serie de ideas y de procesos asociados, como por ejemplo la generalización cartográfica. Esta engloba los procedimientos que permiten que a cada escala se represente la información de la forma más adecuada posible, maximizando el valor de dichas representaciones. Aunque tanto la escala como la generalización cartográfica son conceptos muy vinculados a las propias representaciones visuales de la información geográfica, y este libro contiene una parte dedicada específicamente a la visualización, se trata de conceptos cartográficos fundamentales y por ello se incluyen en este capítulo, ya que resultan necesarios incluso si se trabaja con datos georreferenciados sin visualización alguna de estos.

Conceptos geodésicos básicos

A la hora de definir la forma y dimensiones de la Tierra, la geodesia plantea modelos que puedan recoger la complejidad natural de la superficie terrestre y expresarla de una forma más simple y fácil de manejar.

Con estos modelos, uno de los objetivos principales de la geodesia es establecer un sistema de referencia y definir un conjunto de puntos (conocidos como vértices geodésicos ) cuyas coordenadas en dicho sistema sean conocidas con una precisión elevada. Posteriormente, y en base a esos puntos, los cuales forman una red geodésica , se pueden calcular las coordenadas de cualquier punto en el sistema de referencia definido.

Los vértices geodésicos se establecen por triangulación a partir de un punto único determinado por métodos astronómicos. En función de la longitud de los lados de los triángulos empleados en dicha triangulación, tenemos redes de mayor o menor precisión.

Veamos ahora cómo establecer los elementos necesarios para establecer ese sistema de referencia base y definir esos modelos de partida citados. A la hora de buscar un modelo al que asimilar la forma de la Tierra, existen dos conceptos básicos: el elipsoide de referencia y el geoide .

Elipsoide de referencia y geoide

El intento más básico de establecer un modelo de la forma de la Tierra es asimilar esta a una figura geométrica simple, la cual pueda expresarse mediante una ecuación matemática. Además de ser más sencilla de manejar, disponer de esta ecuación matemática permite la aplicación de conceptos geométricos, estableciendo así una base práctica para el trabajo con coordenadas y la definición de sistemas de referencia.

Desde la antigüedad, se han formulado numerosas hipótesis sobre la forma que la Tierra tenía, las cuales van desde suponer la Tierra plana a admitir la evidencia de que esta ha de tener forma esférica (o similar) si se atiende a diversos hechos como, por ejemplo, el movimiento circular de las estrellas o la existencia de horizonte.

En realidad, la Tierra no es una esfera perfecta, ya que su propia rotación ha modificado esa forma y ha provocado un achatamiento en los polos. Esta hipótesis fue ya planteada por Newton, y corroborada posteriormente con numerosas experiencias. No obstante, podemos seguir tratando de asimilar la forma de la Tierra a la de una superficie teórica, aunque no ya la de una esfera, sino la de lo que se denomina un elipsoide . Sobre un elipsoide, el radio de la Tierra ya no es constante, sino que depende del emplazamiento.

Suponer que la Tierra es una esfera no es una aproximación tan mala como puede parecer (las representaciones gráficas a las que estamos acostumbrados exageran habitualmente mucho el achatamiento del planeta), aunque el elipsoide es más preciso y necesario a la hora de elaborar cartografía de zonas no muy extensas. A gran escala, sin embargo, y para determinadas tareas, es habitual suponer la Tierra con una forma perfectamente esférica.

Como se muestra en la figura \ref{Fig:Elipsoide}, un elipsoide viene definido por dos parámetros: el semieje mayor y el semieje menor.

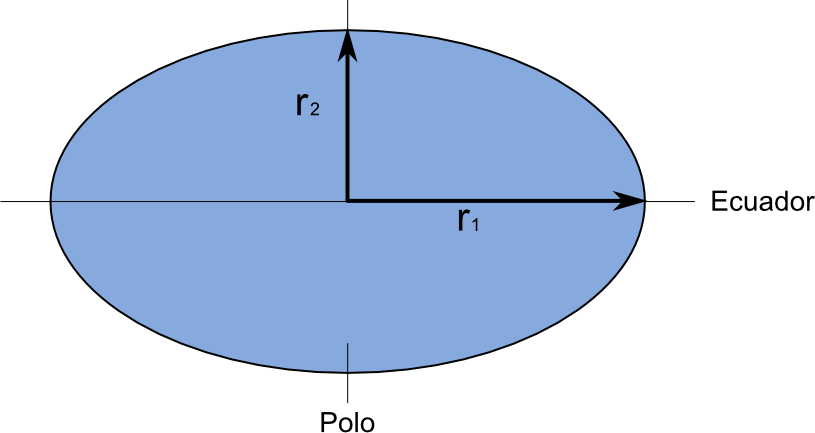
En el caso de la Tierra estos se corresponderían con el radio ecuatorial y el radio polar respectivamente. La relación existente entre estas dos medidas define el grado de achatamiento del elipsoide. En particular, se establece un factor de achatamiento según

\begin{equation} f=\frac{r_1-r_2}{r_1} \end{equation}

siendo $r_1$ el semieje mayor y $r_2$ el semieje menor.

El elipsoide es la forma geométrica que mejor se adapta a la forma real de la Tierra, y por tanto la que mejor permite idealizar esta, logrando un mayor ajuste.

Una vez que se dispone de una expresión teórica para la forma de la Tierra, el siguiente paso es la determinación de los parámetros que definen esta. En el caso de utilizar la esfera, hay que calcular su radio. En el caso de asumir el elipsoide como forma de referencia, deben determinarse las medidas de los semiejes menor y mayor.

Debido a la evolución histórica de la idea de elipsoide de referencia, las medidas de los semiejes que lo definen no son únicas. Es decir, no en todos lugares y en todas las circunstancias se emplea un mismo elipsoide caracterizado por unos valores $r_1$ y $r_2$ idénticos. Esto es debido principalmente al hecho de que un determinado elipsoide no se adapta de modo igualmente preciso a todas las regiones terrestres, y el elipsoide que proporciona un mejor ajuste para un área dada (por ejemplo, un continente o país) puede no ser el mejor en otra zona de la Tierra alejada de la primera.

A esto debe sumarse que los esfuerzos iniciales por determinar la forma de la Tierra y los parámetros del elipsoide de referencia fueron realizados en tiempos en los que la comunicación entre distintos puntos de la superficie terrestre no era la misma que hoy en día. Por ejemplo, los geodestas europeos de entonces realizaban un trabajo similar a sus colegas americanos, pero los datos con los que contaban eran bien distintos, pues las mediciones de cada grupo eran relativas a sus zonas de trabajo, al no resultar sencillo desplazarse a otras partes del planeta a realizar una labor similar.

De este modo, los geodestas de Europa tomaban sus datos y ajustaban a estos sus elipsoides, mientras que los de América hacían un trabajo similar y obtenían sus propios elipsoides. A la hora de establecer un elipsoide de referencia oficial, en cada zona (ya sea administrativa o geográfica) se tomaba el más idóneo, que no era el mismo en todas ellas.

Si añadimos las diferencias tecnológicas y metodológicas que también existían en el proceso de recogida y procesado de datos, es fácil comprender que tengamos una larga serie de elipsoides, cada uno de los cuales ha sido empleado de forma regular en un país o grupo de países, o incluso a escala continental, pero no a nivel global.

La tabla \ref{Tabla:Elipsoides} muestra algunos de los elipsoides de uso más extendido en diversas partes del mundo, con sus correspondientes parámetros.

Elipsoide	Semieje mayor	Semieje menor	$\frac{1}{f}$
Australian National	6378160.000	6356774.719	298.250000
Bessel 1841	6377397.155	6356078.963	299.152813
Clarke 1866	6378206.400	6356583.800	294.978698
Clarke 1880	6378249.145	6356514.870	293.465000
Everest 1956	6377301.243	6356100.228	300.801700
Fischer 1968	6378150.000	6356768.337	298.300000
GRS 1980	6378137.000	6356752.314	298.257222
International 1924 (Hayford)	6378388.000	6356911.946	297.000000
SGS 85	6378136.000	6356751.302	298.257000
South American 1969	6378160.000	6356774.719	298.250000
WGS 72	6378135.000	6356750.520	298.260000
WGS 84	6378137.000	6356752.314	298.257224

Algunos elipsoides y sus parámetros característicos

$$\label{Tabla:Elipsoides}$$

La necesidad de trabajar con un elipsoide global para todo el planeta es más reciente, pero desde hace ya casi un siglo resulta evidente que debe realizarse un esfuerzo por homogeneizar el uso de elipsoides, de tal modo que pueda trabajarse con una referencia internacional que facilite el uso de cartografía en las distintas zonas del planeta. Como consecuencia de esto, surgen los primeros elipsoides generales (en contraste con los elipsoides locales ), los cuales, además de buscar un ajuste óptimo, han de cumplir las siguientes características:

El centro de gravedad terrestre y el del elipsoide deben coincidir.
El plano ecuatorial terrestre y el del elipsoide deben coincidir.

El elipsoide WGS--84 es uno de los más empleados en la actualidad, ya que es el utilizado por el sistema GPS (apartado GPS ).

El geoide es la otra superficie de referencia, definida como la superficie tridimensional en cuyos puntos la atracción gravitatoria es constante. Se trata de una superficie equipotencial que resulta de suponer los océanos en reposo y a un nivel medio (el nivel es en realidad variable como consecuencia de las mareas, corrientes y otros fenómenos) y prolongar estos por debajo de la superficie terrestre. La particularidad del geoide reside en que en todos sus puntos la dirección de la gravedad es perpendicular a su superficie.

El geoide no es, sin embargo, una superficie regular como el elipsoide, y presenta protuberancias y depresiones, como puede observarse en la figura \ref{Fig:Geoide}. La densidad de la Tierra no es constante en todos sus puntos, y ello da lugar a que el geoide sea una superficie irregular como consecuencia de las anomalías gravimétricas que dichas variaciones de densidad ocasionan.

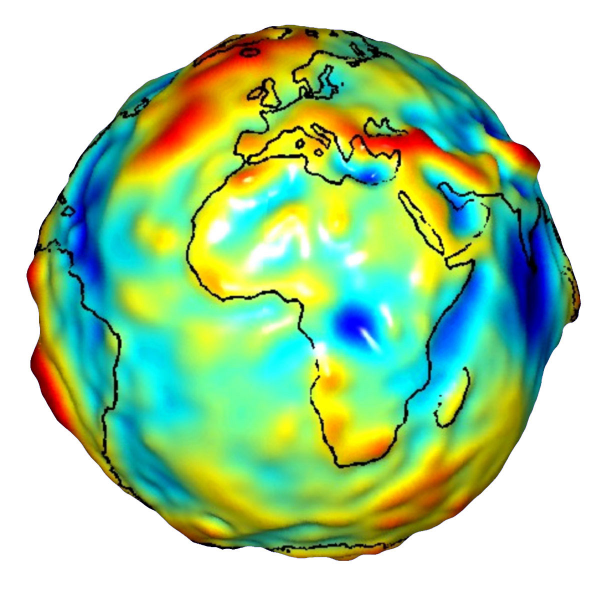
Representación gráfica del geoide (Fuente: Misión GRACE (NASA)).

Lógicamente, el elipsoide, por su naturaleza más simple, no puede recoger toda la variabilidad del geoide, por lo que estas dos superficies presentan diferencias, cuyo máximo es generalmente del orden de $\pm100$ metros. Estas diferencias se conocen como alturas geoidales .

Al igual que en el caso de los elipsoides, existen diversos geoides de referencia, y estos no son constantes en el tiempo, sino que evolucionan para adaptarse a las modificaciones que tienen lugar sobre la superficie terrestre.

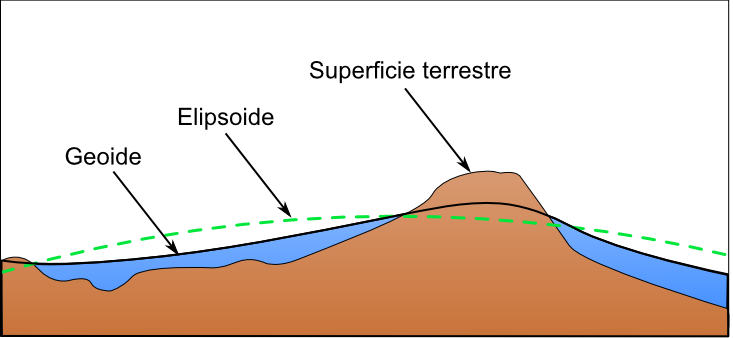
La figura \ref{Fig:Tres_superficies} muestra una comparación esquemática entre las tres superficies: superficie real de la Tierra, geoide y elipsoide.

Tres superficies fundamentales: superficie real de la Tierra, geoide y elipsoide (Adaptado de Wikipedia).

El datum geodésico

Cuando se trabaja con un elipsoide general, este, como se ha dicho, se sitúa de tal modo que tanto la posición de su centro de gravedad como su plano ecuatorial coincidan con los terrestres. Por el contrario, cuando el elipsoide es local, estas propiedades no han de cumplirse necesariamente, y el elipsoide a solas resulta insuficiente ya que carecemos de información sobre su posicionamiento con respecto a la superficie terrestre.

Surge así el concepto de datum , que es el conjunto formado por una superficie de referencia (el elipsoide) y un punto en el que «enlazar» este al geoide. Este punto se denomina punto astronómico fundamental (para su cálculo se emplean métodos astronómicos), o simplemente punto fundamental , y en él el elipsoide es tangente al geoide. La altura geoidal en este punto es, como cabe esperar, igual a cero. La vertical al geoide y al elipsoide son idénticas en el punto fundamental.

Para un mismo elipsoide pueden utilizarse distintos puntos fundamentales, que darán lugar a distintos datum y a distintas coordenadas para un mismo punto.

Sistemas de coordenadas

Disponiendo de un modelo preciso para definir la forma de la Tierra, podemos establecer ya un sistema de codificar cada una de las posiciones sobre su superficie y asignar a estas las correspondientes coordenadas. Puesto que la superficie de referencia que consideramos es un elipsoide, lo más lógico es recurrir a los elementos de la geometría esférica y utilizar estos para definir el sistema de referencia. De ellos derivan los conceptos de latitud y longitud, empleados para establecer las coordenadas geográficas de un punto.

No obstante, la geometría plana resulta mucho más intuitiva y práctica que la geometría esférica para realizar ciertas tareas, y a raíz de esto surgen las proyecciones cartográficas , que tratan de situar los elementos de la superficie del elipsoide sobre una superficie plana, y que son los que se emplean para la creación de cartografía. Al aplicar una proyección cartográfica, las coordenadas resultantes son ya coordenadas cartesianas.

Ambas formas de expresar la posición de un punto se utilizan en la actualidad, y las veremos con detalle en esta sección.

Coordenadas geográficas

El sistema de coordenadas geográficas es un sistema de coordenadas esféricas mediante el cual un punto se localiza con dos valores angulares:

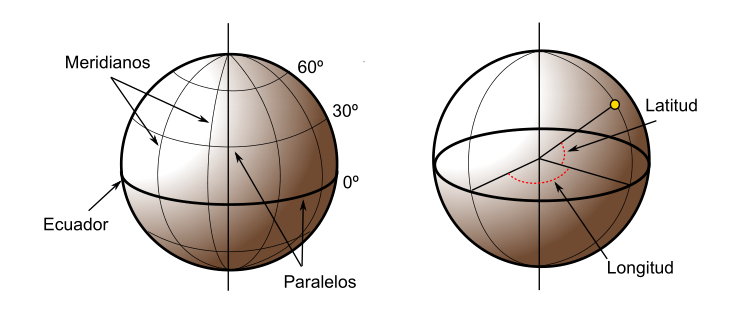
la latitud $\phi$ es el ángulo entre la línea que une el centro de la esfera con un punto de su superficie y el plano ecuatorial. Las líneas formadas por puntos de la misma latitud se denominan paralelos y forman círculos concéntricos paralelos al ecuador. Por definición, la latitud es de 0° en el ecuador, que divide el globo en los hemisferios norte y sur. La latitud puede expresarse especificando si el punto se sitúa al norte o al sur, por ejemplo 24°, 21' 11'' N, o bien utilizando un signo, en cuyo caso los puntos al Sur del ecuador tienen signo negativo.
la longitud $\lambda$ es el angulo formado entre dos de los planos que contienen a la línea de los Polos. El primero es un plano arbitrario que se toma como referencia y el segundo es el que, ademas de contener a la línea de los polos, contiene al punto en cuestión. Las líneas formadas por puntos de igual longitud se denominan meridianos y convergen en los polos. Como meridiano de referencia internacional se toma aquel que pasa por el observatorio de Greenwich, en el Reino Unido. Este divide a su vez el globo en dos hemisferios: el este y el oeste. La longitud puede expresarse especificando si el punto se sitúa al Este o al Oeste, por ejemplo 32°, 12' 43'' E, o bien utilizando un signo, en cuyo caso los puntos al Oeste del meridiano de referencia tienen signo negativo.

En la figura \ref{Fig:Coordenadas_geograficas} puede verse un esquema de los conceptos anteriores.

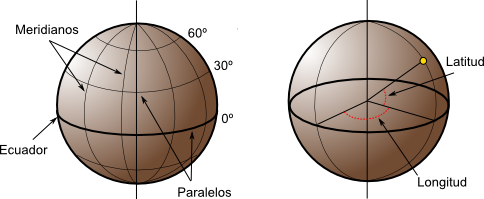
Esquema de los elementos del sistema de coordenadas geográficas.

Las coordenadas geográficas resultan de gran utilidad, especialmente cuando se trabaja con grandes regiones. No obstante, no se trata de un sistema cartesiano, y tareas como la medición de áreas o distancias es mucho más complicada. Si bien la distancia entre dos paralelos es prácticamente constante (es decir, un grado de latitud equivale más o menos a una misma distancia en todos los puntos), la distancia entre dos meridianos no lo es, y varía entre unos 11,3 kilómetros en el Ecuador hasta los cero kilómetros en los polos, donde los meridianos convergen.

Proyecciones cartográficas

A pesar de su innegable utilidad y la potencia que nos brindan para la localización de cualquier punto sobre la superficie terrestre, un sistema de coordenadas esféricas tiene inconvenientes que no pueden obviarse. Por una parte, estamos más acostumbrados a la utilización de sistemas cartesianos en los cuales la posición de un punto se define mediante un par de medidas de distancia $x$ e $y$. Por otro lado, si necesitamos crear una representación visual de la información cartográfica, lo habitual es hacerlo en una superficie plana, ya sea a la manera clásica en un pliego de papel o, usando las tecnologías actuales, en un dispositivo tal como una pantalla.

Por todo ello, se deduce que existe una necesidad de poder trasladar la información geográfica (incluyendo, por supuesto, la referente a su localización) a un plano, con objeto de poder crear cartografía y simplificar gran número de operaciones posteriores. El proceso de asignar una coordenada plana a cada punto de la superficie de la Tierra (que no es plana) se conoce como proyección cartográfica .

Más exactamente, una \textit{proyección cartográfica} es la correspondencia matemática biunívoca entre los puntos de una esfera o elipsoide y sus transformados en un plano [ Martin1983IGN ]. Es decir, una aplicación $f$ que a cada par de coordenadas geográficas $(\phi, \lambda)$ le hace corresponder un par de coordenadas cartesianas $(x, y)$, según

\begin{equation} \label{Eq:Proyecciones} x = f(\phi, \lambda) \; ; \; y = f(\phi, \lambda) \end{equation}

De igual modo, las coordenadas geográficas puede obtenerse a partir de las cartesianas según

\begin{equation} \label{Eq:Proyecciones2} \phi = g(x,y) \; ; \; \lambda = g(x,y) \end{equation}

Se puede pensar que podemos obtener una representación plana de la superficie de una esfera o un elipsoide si tomamos esta y la extendemos hasta dejarla plana. Esto, sin embargo, no resulta posible, ya que dicha superficie no puede desarrollarse y quedar plana. Por ello, hay que buscar una forma distinta de relacionar los puntos en la superficie tridimensional con nuevos puntos en un plano.

La figura \ref{Fig:Proyeccion} muestra un esquema del concepto de proyección, esbozando la idea de cómo puede establecerse la correspondencia entre puntos de la esfera y del plano.

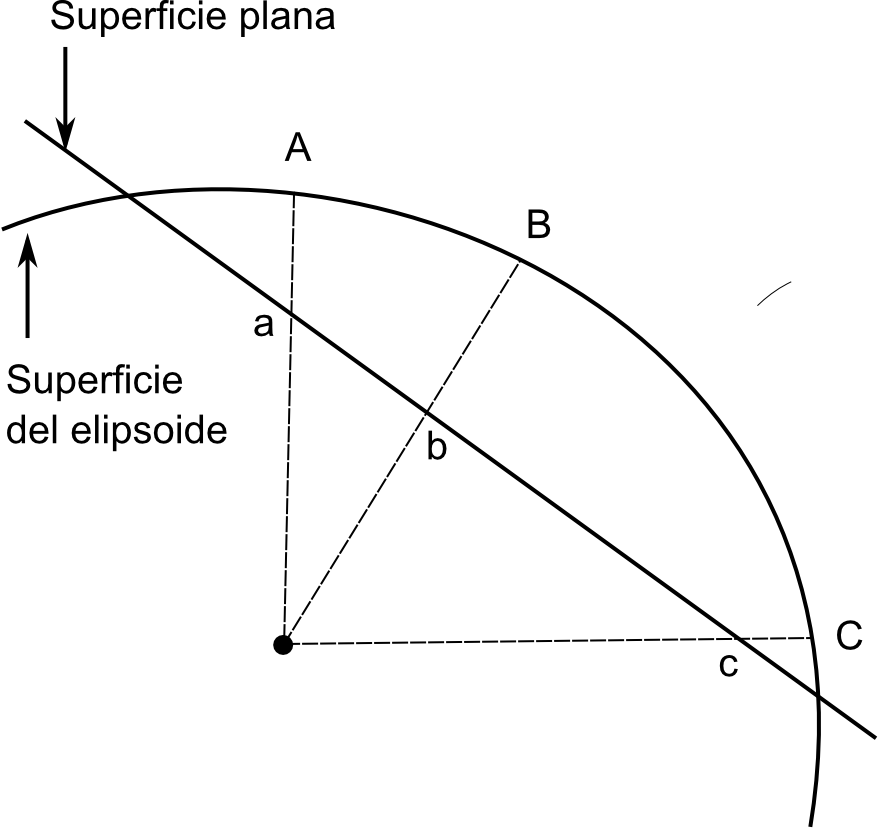
Esquema del concepto de proyección. A los puntos $A, B$ y $C$ sobre la superficie del elipsoide les asocian equivalentes $a, b$ y $c$ sobre un plano.

En ella vemos cómo el concepto de proyección se asemeja a la generación de sombras, ya que a partir de un foco se trazan las trayectorias de una serie de rayos que unen dicho foco con los puntos a proyectar, y después se determina el punto de contacto de esos rayos con la superficie plana. Aunque no todas las proyecciones siguen necesariamente este esquema, una parte de ellas sí que se fundamentan en un razonamiento similar a este, y el esquema mostrado sirve bien para entender el concepto y el paso de coordenadas de una superficie tridimensional a una bidimensional.

Veremos en los siguientes puntos las diferentes modificaciones que pueden introducirse sobre la forma anterior de proyectar, y que dan lugar a tipos distintos de proyecciones.

Puede apreciarse igualmente en la figura que se producen distorsiones al realizar la proyección. Es decir, que ciertas propiedades no se reproducen con fidelidad al pasar puntos desde la superficie curva al plano. Por ejemplo, la distancia entre los puntos $A$ y $B$ no es igual a la existente entre los puntos $a$ y $b$. Con independencia de las características propias de la proyección, siempre existen distorsiones. Esto es así debido a que la esfera, como se ha dicho, no es desarrollable, mientras que el plano sí lo es, y por ello en el paso de coordenadas de uno a otra han de aparecen inevitablemente alteraciones.

Tipos de proyecciones

Las proyecciones se clasifican según la superficie sobre la que se proyectan los puntos. En el esquema de la figura \ref{Fig:Proyeccion}, el plano de proyección es ya de por sí bidimensional. No obstante, puede realizarse la proyección sobre una superficie tridimensional, siempre que esta, a diferencia de la esfera, sí sea desarrollable. Es decir, que pueda «desenrollarse» y convertirse en un plano sin necesidad de doblarse o cortarse. Estas otras superficies pueden emplearse también para definir una proyección, de la misma forma que se hace con un plano.

Esquema de una proyección cónica (izda.) y cilíndrica(dcha.)

Las superficies más habituales son el cono y el cilindro (junto con, por supuesto, el plano), las cuales, situadas en una posición dada en relación con el objeto a proyectar (esto es, la Tierra), definen un tipo dado de proyección. Distinguimos así los siguiente tipos de proyecciones:

Cónicas . La superficie desarrollable es un cono (Figura \ref{Fig:Proyeccion_conica_cilindrica}), que se sitúa generalmente tangente o secante en dos paralelos a la superficie del elipsoide. En este último caso, la distorsión se minimiza en las áreas entre dichos paralelos, haciéndola útil para representar franjas que no abarquen una gran distancia en latitud, pero poco adecuada para representación de grandes áreas. Algunas de las proyecciones más conocidas de este grupo son la proyección cónica equiárea de Albers y la proyección conforme cónica de Lambert.
Cilíndricas . La superficie desarrollable es un cilindro (Figura \ref{Fig:Proyeccion_conica_cilindrica}). Al proyectar, los meridianos se convierten en líneas paralelas, así como los paralelos, aunque la distancia entre estos últimos no es constante.
En su concepción más simple, el cilindro se sitúa de forma tangente al ecuador (proyección normal o simple), aunque puede situarse secante y hacerlo a los meridianos (proyección transversa) o a otros puntos (proyección oblicua).

La proyección de Mercator, la transversa de Mercator, la cilíndrica de Miller o la cilíndrica equiárea de Lambert son ejemplos relativamente comunes de este tipo de proyecciones.
Planas o azimutales . La superficie desarrollable es directamente un plano. Según el esquema de la figura \ref{Fig:Proyeccion}, tenemos distintos tipos en función de la posición del punto de fuga.
- Gnómica o central. El punto de fuga se sitúa en el centro del elipsoide.
- Estereográfica. El plano es tangente y el punto de fuga se sitúa en las antípodas del punto de tangencia. La proyección polar estereográfica es empleada habitualmente para cartografiar las regiones polares.
- Ortográfica. El punto de fuga se sitúa en el infinito.
Existen proyecciones azimutales que no son de tipo perspectivo, es decir, que no se basan en el esquema de la figura \ref{Fig:Proyeccion}. La proyección de Airy, por ejemplo, es una de ellas.
Algunas proyecciones no se ajustan exactamente al esquema planteado , y no utilizan una superficie desarrollable como tal sino modificaciones a esta idea. Por ejemplo, las proyecciones policónicas utilizan la misma filosofía que las cónicas, empleando conos, pero en lugar de ser este único, se usan varios conos, cada uno de los cuales se aplica a una franja concreta de la zona proyectada. La unión de todas esas franjas, cada una de ellas proyectada de forma distinta (aunque siempre con una proyección cónica), forma el resultado de la proyección.
Del mismo modo, encontramos proyecciones como la proyección sinusoidal , una proyección de tipo pseudocilíndrico, o la proyección de Werner, cuya superficie desarrollable tiene forma de corazón. Estas proyecciones son, no obstante, de uso menos habitual, y surgen en algunos casos como respuesta a una necesidad cartográfica concreta.

Otra forma distinta de clasificar las proyecciones es según las propiedades métricas que conserven. Toda proyección implica alguna distorsión (denominada anamorfosis ), y según cómo sea esta y a qué propiedad métrica afecte o no, podemos definir los siguientes tipos de proyecciones:

Equiárea . En este tipo de proyecciones se mantiene una escala constante. Es decir, la relación entre un área terrestre y el área proyectada es la misma independientemente de la localización, con lo que la representación proyectada puede emplearse para comparar superficies.
Conformes . Estas proyecciones mantienen la forma de los objetos, ya que no provocan distorsión de los ángulos. Los meridianos y los paralelos se cortan en la proyección en ángulo recto, igual que sucede en la realidad. Su principal desventaja es que introducen una gran distorsión en el tamaño, y objetos que aparecen proyectados con un tamaño mucho mayor que otros pueden ser en la realidad mucho menores que estos.
Equidistantes . En estas proyecciones se mantienen la proporcionalidad de las distancias.

En los ejemplos de proyecciones que se han citado para los distintos tipos de proyecciones (cónicas, cilíndricas, etc.), puede verse cómo resulta común especificar el tipo en función de la propiedad métrica preservada, para así caracterizar completamente la proyección.

La elección de una u otra proyección es función de las necesidades particulares. Como ya se ha dicho, la proyección polar estereográfica es empleada cuando se trabaja las regiones polares, ya que en este caso es la más adecuada. Proyecciones como la de Mercator, empleadas habitualmente, no resultan tan adecuadas en esas zonas. Asimismo, hay proyecciones que no pueden recoger todo el globo, sino solo una parte de este, por lo que no son de aplicación para pequeñas escalas. La existencia de un gran número de distintas proyecciones es precisamente fruto de las diferentes necesidades que aparecen a la hora de trabajar con cartografía.

El sistema UTM

De entre los cientos de proyecciones que existen actualmente, algunas tienen un uso más extendido, bien sea por su adopción de forma estandarizada o sus propias características. Estas proyecciones, que se emplean con más frecuencia para la creación de cartografía, son también las que más habitualmente vamos a encontrar en los datos que empleemos con un SIG, y es por tanto de interés conocerlas un poco más en detalle.

En la actualidad, una de las proyecciones más extendidas en todos los ámbitos es la proyección universal transversa de Mercator, la cual da lugar al sistema de coordenadas UTM. Este sistema, desarrollado por el ejército de los Estados Unidos, no es simplemente una proyección, sino que se trata de un sistema completo para cartografiar la practica totalidad de la Tierra. Para ello, esta se divide en una serie de zonas rectangulares mediante una cuadricula y se aplica una proyección y unos parámetros geodésicos concretos a cada una de dichas zonas. Aunque en la actualidad se emplea un único elipsoide (WGS--84), originalmente este no era único para todas las zonas.

Con el sistema UTM, las coordenadas de un punto no se expresan como coordenadas terrestres absolutas, sino mediante la zona correspondiente y las coordenadas relativas a la zona UTM en la que nos encontremos.

La cuadricula UTM tiene un total de 60 husos numerados entre 1 y 60, cada uno de los cuales abarca una amplitud de 6° de longitud. El huso 1 se sitúa entre los 180° y 174° O, y la numeración avanza hacia el Este.

En latitud, cada huso se divide en 20 zonas, que van desde los 80° S hasta los 84° N. Estas se codifican con letras desde la C a la X, no utilizándose las letras I y O por su similitud con los dígitos 1 y 0. Cada zona abarca 8 grados de longitud, excepto la X que se prolonga unos 4 grados adicionales.

Una zona UTM se localiza, por tanto, con un número y una letra, y es en función de la zona como posteriormente se dan las coordenadas que localizan un punto. Estas coordenadas se expresan en metros y expresan la distancia entre el punto y el origen de la zona UTM en concreto. El origen de la zona se sitúa en el punto de corte entre el meridiano central de la zona y el ecuador. Por ejemplo, para las zonas UTM en el huso 31, el cual va desde los 0° hasta los 6°, el origen se sitúa en el punto de corte entre el ecuador y el meridiano de 3° (Figura \ref{Fig:Origen_UTM}).

Determinación del origen de una zona UTM

Para evitar la aparición de números negativos, se considera que el origen no tiene una coordenada X de 0 metros, sino de 500000. Con ello se evita que las zonas al Este del meridiano central tengan coordenadas negativas, ya que ninguna zona tiene un ancho mayor de 1000000 metros (el ancho es máximo en las zonas cerca del ecuador, siendo de alrededor de 668 kilómetros).

De igual modo, cuando se trabaja en el hemisferio sur (donde las coordenadas Y serían siempre negativas), se considera que el origen tiene una coordenada Y de 10000000 metros, lo cual hace que todas las coordenadas referidas a él sean positivas.

La figura \ref{Fig:Zonas_UTM} muestra un esquema de la cuadrícula UTM.

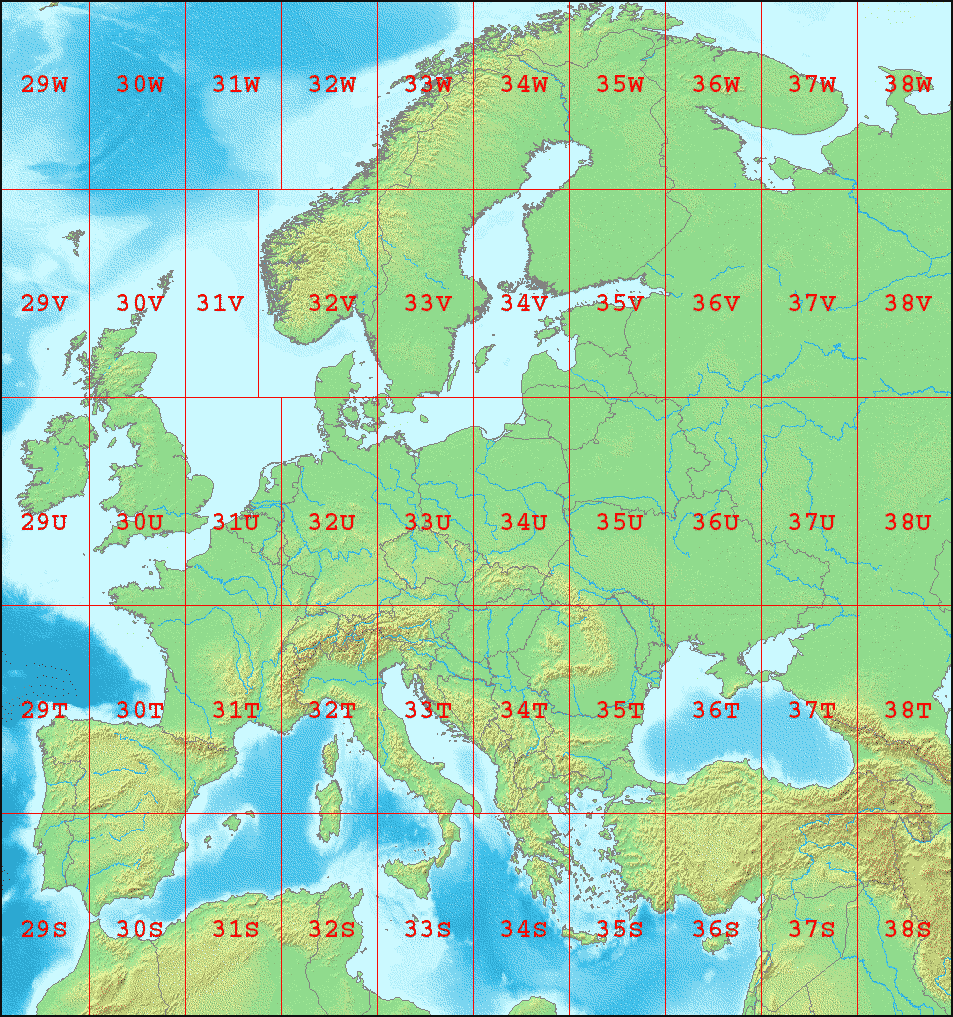
Representación parcial de la cuadrícula UTM en Europa (tomado de Wikipedia)

Para las zonas polares no resulta adecuado emplear el sistema UTM, ya que las distorsiones que produce son demasiado grandes. En su lugar, se utiliza el sistema UPS (Universal Polar Stereographic).

Transformación y conversión de coordenadas

Una situación muy habitual en el trabajo con un SIG es disponer de cartografía en varios sistemas de coordenadas, o bien en un mismo sistema pero con parámetros diferentes (por ejemplo, diferente datum). Para poder emplear toda esa cartografía de forma conjunta, resulta necesario trabajar en un sistema único y bien definido, lo cual hace necesario convertir al menos una parte de ella.

Este cambio de coordenadas puede ser obligatorio a cualquier escala de trabajo, ya que las diferencias en el sistema escogido pueden aparecer por circunstancias muy diversas, incluso si todos los datos tienen un origen común. Así, al reunir información de varios países para crear en un SIG un mapa de todo un continente, es probable que los datos de cada país estén referidos a un sistema distinto, pero incluso trabajando en un área más reducida podemos encontrar una situación similar. En España, por ejemplo, podemos encontrar cartografía de algunas Comunidades Autónomas en dos husos UTM distintos, ya que la frontera entre estos cruza y divide dichas Comunidades.

Distinguimos dos tipos de operaciones a realizar con coordenadas:

Conversión de coordenadas . Los sistemas de origen y destino comparten el mismo datum. Es una transformación exacta y se basa en la aplicación de formulas establecidas que relacionan ambos sistemas.
Transformación de coordenadas . El datum es distinto en los sistemas de origen y destino.

Las proyecciones cartográficas, vistas en un punto anterior, son una forma particular de conversión de coordenadas.

Un SIG ha de estar preparado para trabajar con cartografía en cualquiera de los sistemas de referencia más habituales y, más aún, para facilitar al usuario la utilización de todo tipo de información geográfica con independencia del sistema de coordenadas que se emplee. Para ello, los SIG incorporan los procesos necesarios para efectuar cambios de coordenadas, de forma que para unos datos de partida se genera un nuevo conjunto de datos con la misma información pero expresada en un sistema de coordenadas distinto.

Otra forma en la que los SIG pueden implementar estas operaciones es mediante capacidades de transformación y conversión «al vuelo», es decir, en tiempo real. De este modo, pueden introducirse en un SIG datos en sistemas de coordenadas variados, y el SIG se encarga de cambiar estos a un sistema de referencia base fijado de antemano. Este proceso tiene lugar de forma transparente para el usuario, que tiene la sensación de que todos los datos estaban originalmente en el sistema de trabajo escogido.

Esto exige, lógicamente, que todo dato geográfico se acompañe de información acerca del sistema de coordenadas que se ha utilizado para crearlo, algo que no siempre sucede. Veremos más acerca de la importancia de este tipo de información adicional en el capítulo Metadatos .

Codificación de sistemas de referencia

Debido al elevado número de distintos sistemas de referencia existentes, resulta fácil perderse en ellos a la hora de tener que trabajar con cartografía en distintos sistemas. Si bien es cierto que existe un esfuerzo integrador para tratar de homogeneizar el uso de sistemas de referencia, también existen esfuerzos para intentar facilitar la gestión de estos y que no resulte tan complejo combinar cartografía producida utilizando sistemas de coordenadas diferentes.

Uno de los intentos más exitosos en este sentido es el desarrollado por el consorcio petrolífero European Petroleum Survey Group (EPSG), el cual, consciente de la necesidad de disponer de información acerca de los distintos sistemas de coordenadas y de que esta información fuera de fácil acceso y manejo, ha elaborado un esquema de codificación específico.

Este esquema asocia a cada sistema de coordenadas un código (conocido como código EPSG ) que la identifica. Paralelamente, se han documentado en un formato común las características principales de todos estos sistemas, así como las formulaciones que permiten transformar coordenadas entre ellos.

Esta información constituye el EPSG geodetic parameter dataset , un repositorio de los parámetros necesarios para

identificar coordenadas de tal modo que estas describan la posición de un punto de forma inequívoca y no ambigua.
definir transformaciones y conversiones que permitan pasar de un sistema de referencia a otro.

Escala

El concepto de escala es fundamental a la hora de trabajar con cartografía, y es uno de los valores básicos que definen toda representación cartográfica. Esta representación ha de tener un tamaño final manejable, con objeto de que pueda resultar de utilidad y permitir un uso práctico, pero el objeto que se cartografía (un país, un continente o bien la Tierra al completo) es un objeto de gran tamaño. Esto hace necesario que, para crear un mapa, se deba reducir o bien el objeto original o bien el objeto ya proyectado, dando lugar a una versión «reducida» que ya cumple con los requisitos de tamaño adecuado.

Es decir, imaginemos que aplicamos una proyección cónica sobre el elipsoide, empleando para ello un cono que cubra dicho elipsoide. Este cono tendrá que ser, lógicamente, de gran tamaño. Al desarrollarlo, el plano que obtenemos tendrá miles de kilómetros de lado. Debemos fabricar una versión «a escala» de este, que será la que ya podamos utilizar.

En este contexto, la escala no es sino la relación de tamaño existente entre ese gran mapa que se obtiene al desarrollar nuestro cono de proyección y el que finalmente manejamos, de tamaño más reducido. Conociendo esta relación podemos ya conocer las verdaderas magnitudes de los elementos que vemos en el mapa, ya que podemos convertir las medidas hechas sobre el mapa en medidas reales. Es importante recordar que esas medidas no son tan «reales», puesto que la propia proyección las ha distorsionado —lo cual no debe olvidarse—, pero sí que son medidas en la escala original del objeto cartografiado.

La escala se expresa habitualmente como un denominador que relaciona una distancia medida en un mapa y la distancia que esta medida representa en la realidad. Por ejemplo, una escala 1:50000 quiere decir que 1 centímetro en un mapa equivale a 50000 centímetros en la realidad, es decir, a 500 metros. Conociendo este valor de la escala podemos aplicar sencillas reglas de tres para calcular la distancia entre dos puntos o la longitud de un elemento dado, sin más que medirlo sobre el mapa y después convertir el resultado obtenido en una medida real.

Una vez más es preciso insistir que lo anterior es posible siempre bajo las limitaciones que la propia proyección empleada para crear el mapa tenga al respecto, y que dependerán del tipo de proyección que sea en función de las propiedades métricas que conserva.

De hecho, e independientemente del tipo de proyección, la escala es completamente cierta únicamente en determinadas partes del mapa. Cuando decimos que un mapa tiene una escala 1:50000, este valor, denominado Escala Numérica , se cumple con exactitud tan solo en algunos puntos o líneas. En otros puntos la escala varía. La relación entre la escala en esos puntos y la Escala Numérica se conoce como Factor de Escala .

A pesar de que la escala es imprescindible para darle un uso práctico a todo mapa, y cualquier usuario de este debe conocer y aplicar el concepto de escala de forma precisa, los SIG pueden resultar engañosos al respecto. Aunque la escala como idea sigue siendo igual de fundamental cuando trabajamos con información geográfica en un SIG, las propias características de este y la forma en la que dicha información se incorpora en el SIG pueden hacer que no se perciba la escala como un concepto tan relevante a la hora de desarrollar actividad con él.

Esto es debido principalmente a que la escala tiene una relación directa con la visualización, ya que se establece entre la realidad y una representación visual particular, esto es, el mapa. Como ya se ha mencionado en el capítulo Introduccion_fundamentos , los datos en un SIG tienen carácter numérico y no visual, y la representación de estos se encarga de realizarla el subsistema correspondiente a partir de dichos datos numéricos. Es decir, que en cierta medida en un SIG no es estrictamente necesaria la visualización de los datos, y cuando esta se lleva a cabo no tiene unas características fijas, ya que, como veremos, el usuario puede elegir el tamaño con el que estos datos se representan en la pantalla.

Un mapa impreso puede ampliarse o reducirse mediante medios fotomecánicos. Sin embargo, no es esta una operación «natural», y está claro que desde el punto de vista del rigor cartográfico no es correcta si lo que se hace es aumentar el tamaño del mapa. En un SIG, sin embargo, es una operación más el elegir la escala a la que se representan los datos y modificar el tamaño de representación, y esta resulta por completo natural e incluso trivial[ Jenerette2000BESA ].

Pese a ello, los datos tienen una escala inherente, ya que esta no está en función de la representación, sino del detalle con que han sido tomados, y esta escala debe igualmente conocerse para dar un uso adecuado a dichos datos. En este sentido es más conveniente entender la escala como un elemento relacionado con la resolución de los datos, es decir, con el tamaño mínimo cartografiado.

Esta concepción no es en absoluto propia de los SIG, ya que deriva de las representaciones clásicas y los mapas impresos. Se sabe que el tamaño mínimo que el ojo humano es capaz de diferenciar es del orden de 0,2 mm. Aplicando a este valor la escala a la que queremos crear un mapa, tendremos la mínima distancia sobre el terreno que debe medirse. Por ejemplo, para el caso de un mapa 1:50000, tenemos que la mínima distancia es de 10 metros.

Si medimos puntos a una distancia menor que la anterior y después los representamos en un mapa a escala 1:50000, esos puntos no serán distinguibles para el usuario de ese mapa, y la información recogida se perderá. Estos razonamientos sirven para calcular la intensidad del trabajo que ha de realizarse para tomar los datos con los que después elaborar una determinada cartografía.

En realidad, el concepto de escala no es único, sino que tiene múltiples facetas. Por una parte la escala cartográfica , que es la mera relación entre el tamaño en el mapa y la realidad. Por otra, la escala de análisis u operacional [ Lam1992PG ], que es la que define la utilidad de los datos y lo que podemos hacer con ellos, ya que indica las limitaciones de estos. Cuando en un SIG aumentamos el tamaño en pantalla de una cierta información geográfica, estamos variando la escala cartográfica, pero no estamos modificando la escala de análisis. Por ello, por mucho que ampliemos, no vamos a ver más detalles, ya que para ello sería necesario tomar más datos.

Veremos más ideas sobre la escala de análisis y algunas implicaciones al respecto en el capítulo Introduccion_procesos , al inicio de la parte dedicada a los procesos, ya que estos conceptos son fundamentales para realizar correctamente análisis y operaciones como las descritas en esa parte del libro.

Un tipo de datos espaciales particulares con los que se trabaja en un SIG, los datos ráster , tienen a su vez un parámetro de resolución, con una clara relación con el concepto de escala. Veremos más al respecto en el capítulo Tipos_datos .

Generalización cartográfica

Muy relacionado con el concepto de escala encontramos la denominada generalización cartográfica . Generalizar implicar expresar alguna idea o información de forma más resumida, de tal modo que esta sea comprensible y pueda aprovecharse de la mejor manera posible. En el ámbito cartográfico, cuando hablamos de generalización nos referimos a la adaptación de los elementos de un mapa para lograr que este sea más expresivo y claro, lo cual puede conllevar una distorsión intencional de dichos elementos.

Para ver un ejemplo de lo anterior, pensemos en un mapa del mundo en el que se representen todas las calles y caminos existentes. Esta información tiene una escala adecuada para ser mostrada en un callejero local cuya escala nominal suele ser del orden de 1:5000, pero a la escala 1:1000000, adecuada para un mapa mundial, representar todo su detalle resulta innecesario. La representación resultante va a tener una densidad excesiva, y muchos de sus elementos no podrán distinguirse debido a su cercanía.

En caso de que esta representación no se haga sobre papel sino sobre una pantalla y trabajando con un SIG, la situación es similar y resulta incluso más necesario aplicar alguna forma de generalización. A las limitaciones de la visión humana han de sumarse las limitaciones de resolución que el propio dispositivo presenta. En la situación del ejemplo anterior, muchos elementos del mapa (calles, edificios, etc.), ocuparían por su tamaño un mismo y único punto en la pantalla (veremos más adelante que cada uno de estos puntos se conoce como píxel ), por lo que resultaría imposible distinguirlos o detallarlos más allá de ese nivel de resolución.

A lo anterior debemos añadir el hecho de que producir esa representación, aunque sea sobre un solo píxel, puede requerir gran cantidad de procesos y operaciones, ya que el conjunto de calles que se contienen en él pueden presentar gran complejidad, tanto mayor cuanto mayor sea el nivel de detalle con que han sido recogidas en los datos. Es decir, que en el trabajo con un SIG la generalización no tiene importancia únicamente para la visualización en sí, sino también para el rendimiento del propio SIG a la hora de producir dicha visualización.

La generalización, en este caso, implicaría la elección de un subconjunto de todas esas carreteras, de manera que no se representase la totalidad de la información de la que se dispone.

En ocasiones, el proceso de generalización es necesario por razones distintas a lo visto en el ejemplo anterior, y requiere diferentes operaciones. Por ejemplo, podemos crear un mapa del mundo que contenga vías de comunicación, pero no todas, sino solo las principales autopistas de cada país. En este caso, no vamos a encontrar problemas con distintas carreteras que se solapan en la representación, ni tampoco un volumen excesivo de datos, pero debemos igualmente «adaptar» la representación a la escala, es decir, efectuar algún tipo de generalización.

Si en ese mapa representamos una carretera con un ancho de 20 metros a escala 1:1000000, el tamaño que tendrá en el mapa será de tan solo 0,02 milímetros. Este ancho es prácticamente nulo, y no tiene sentido representar esa carretera de esta forma. Ha de representarse con un ancho mayor. Aunque no se esté dibujando con exactitud la magnitud real de ese elemento, el resultado es mucho mejor desde todos los puntos de vista. Esta es otra forma de generalización que busca también mejorar la calidad de la representación y la transmisión de la información que contiene.

La generalización, por tanto, es un proceso que tiene como objetivo la producción de una imagen cartográfica legible y expresiva, reduciendo el contenido del mapa a aquello que sea posible y necesario representar. Para ello, se enfatiza aquello que resulta de importancia y se suprime lo que carece de ella [ Anon2002EUITP ].

Operaciones de generalización

Existen diversas operaciones que se emplean en el proceso de generalización. Algunas de las más relevantes son las siguientes [ McMaster1992AAG ]:

Simplificación . Se trata de crear elementos más sencillos que sean más fáciles y rápidos de representar. Los elementos originales se sustituyen por estos más sencillos, de tal modo que se mantienen las características visuales principales pero las operaciones con los datos se optimizan.
Suavizado . Se sustituyen formas angulosas por otras más suaves y de menor complejidad.
Agregación . Un conjunto de varios objetos se sustituye por uno nuevo con un menor número. Por ejemplo, al representar una ciudad, no dibujar cada una de las casas, sino solo el contorno de cada manzana. La figura \ref{Fig:Generalizacion_agregacion} muestra un ejemplo de esta técnica aplicado a elementos lineales, en particular carreteras.
Exageración . En ocasiones, mantener el objeto a la escala que le corresponde haría que no se pudieran apreciar las características de este. En este caso, se exagera su tamaño para que pueda interpretarse con mayor facilidad y no perder información en la representación.
Desplazamiento . Un objeto se representa en una posición distinta a la que le corresponde, con el fin de garantizar su visibilidad y obtener un resultado más claro.

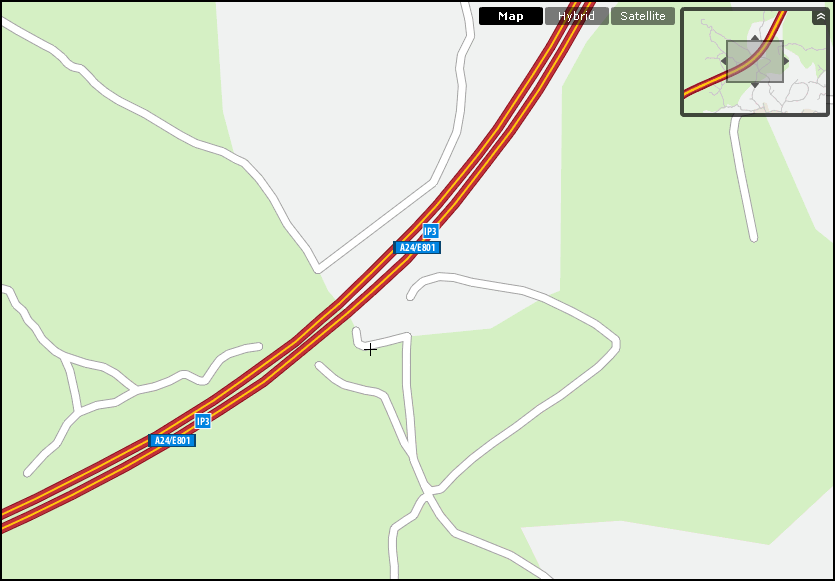
Un ejemplo de generalización por agregación. Dos carreteras prácticamente paralelas y unidas se representan como dos elementos en el mapa, pero en el localizador de la parte superior izquierda, a escala de menor detalle, se generalizan como una única (Tomado de Yahoo Maps).

Combinando operaciones como las anteriores de forma adecuada, se obtiene una cartografía mucho más útil y con mayor potencial. En el caso de trabajar en un SIG, algunas de estas operaciones, como pueden ser la simplificación o la agregación, tiene también un efecto beneficioso sobre el propio manejo de los datos dentro del SIG.

Estas operaciones se enumeran aquí como ideas a aplicar para efectuar la generalización de un documento geográfico, como corresponde a este capítulo de fundamentos y conceptos cartográficos básicos. No obstante, también las veremos en otras partes del libro, ya que no son exclusivas de esta parte. Por su importante papel en la representación visual de los datos, veremos más al respecto en la parte dedicada a visualización. Algunos algoritmos para la simplificación y suavizado de líneas los estudiaremos en la parte dedicada a procesos, particularmente en el apartado Generalizacion_lineas .

Generalización en el contexto de un SIG

La generalización es importante en un SIG debido a la variedad de escalas posibles que puede tener la información con que se trabaja, así como por la variedad de escalas de representación que pueden definirse gracias a la flexibilidad que el propio SIG presenta en sus capacidades de visualización. Existen diversas formas de enfocar inicialmente el problema de obtener un juego de datos óptimo para ser representado en cada caso y una representación óptima de este.

La mayor problemática se encuentra en el manejo de datos con gran precisión y gran volumen —como, por ejemplo, esos datos de calles y vías de todo el mundo— al representarlos a una escala de menor detalle, aunque el proceso de generalización no es necesario exclusivamente en este caso, sino en muchos otros con independencia del volumen y la escala original.

Una aproximación básica puede ser trabajar con todo el conjunto de datos y generalizarlo a medida que sea necesario en función de la escala de trabajo en cada momento. Es decir, si el usuario decide visualizar todo un continente, el SIG no traza todas las calles de ese continente, sino que se seleccionan de forma automática los objetos a representar y después se crea la representación. Las operaciones de generalización se llevan a cabo en el momento mismo en que el usuario lo necesita.

Este tipo de generalización «al vuelo» no resulta, sin embargo, óptimo, y en la mayoría de los casos es inviable o no proporciona los resultados esperados. Esto es así debido a que se ha de trabajar con el gran volumen de datos original, y generalizar estos es una tarea suficientemente compleja como para que los algoritmos encargados de hacerlo no lo hagan de forma fluida. No ha de olvidarse que, mientras que la razón fundamental de la generalización en el contexto de la cartografía clásica es la mera visualización y la transmisión de la información, en el entorno de un SIG también existen razones relacionadas con la eficiencia de los procesos, como ya se ha mencionado. Aplicando esta metodología, la generalización no es ventajosa en términos de cómputo, sino que, por el contrario, puede incluso suponer una carga adicional al proceso de visualización.

Aun en el caso de que el volumen de datos no fuera grande y no existieran problemas de rendimiento, una generalización por completo automatizada no garantiza un resultado óptimo. Pese a que existen algoritmos y formulaciones matemáticas que permiten generalizar de forma relativamente adecuada (algunos de los cuales los veremos más adelante en este libro), el proceso global de generalización combina varios procedimientos distintos, y en conjunto conforma un proceso no exento de subjetividad. La labor tradicional del cartógrafo no puede automatizarse de forma total, y se hace necesario cierto trabajo manual para obtener un resultado de calidad o evaluar el generado por un procedimiento automático.

Por todo lo anterior, la forma de incorporar la generalización dentro de un SIG suele basarse en un enfoque multi--escalar, en el cual se maneja información de una misma zona de estudio a diferentes escalas, y se usa en cada momento aquella que resulte más conveniente. Si trabajara con cartografía en papel, sería equivalente a tener varios mapas de una zona a diferentes escalas.

Por ejemplo, en un mapa con núcleos de población a escala 1:25000 se almacenará cada ciudad como un polígono que delimite su contorno. Esa misma información a escala 1:1000000 se almacenará como un único punto cada ciudad, ya que el tamaño de esta es demasiado pequeño en la representación, y no tiene sentido el empleo de tanto detalle. Para convertir un mapa en otro se ha producido un proceso de simplificación, convirtiendo polígonos en puntos.

Si incorporamos ambos mapas dentro de un SIG, podemos utilizar el que corresponda en función de la escala requerida. De este modo, la generalización no es una tarea que el propio SIG desarrolle, sino que cuando esta es necesaria puede recurrir a una información ya generalizada de antemano. El rendimiento del proceso es mayor, y además el dato generalizado puede haber sido elaborado de la forma más conveniente.

El concepto de capa , que veremos en el capítulo Introduccion_datos y que es vital para la idea actual de un SIG, permite este manejo simultáneo de información a distintas escalas.

En la figura \ref{Fig:SIG_multi_escala} puede verse un esquema de lo anterior. A medida que variamos la escala de representación, la información que vemos representada tiene una escala distinta y podría también tener un distinto origen. Incluso el tipo de información que vemos varía, ya que las representaciones más globales son de tipo gráfico, creadas a partir de los propios datos almacenados como objetos (calles, carreteras, etc.), mientras que la de mayor detalle es una fotografía aérea.

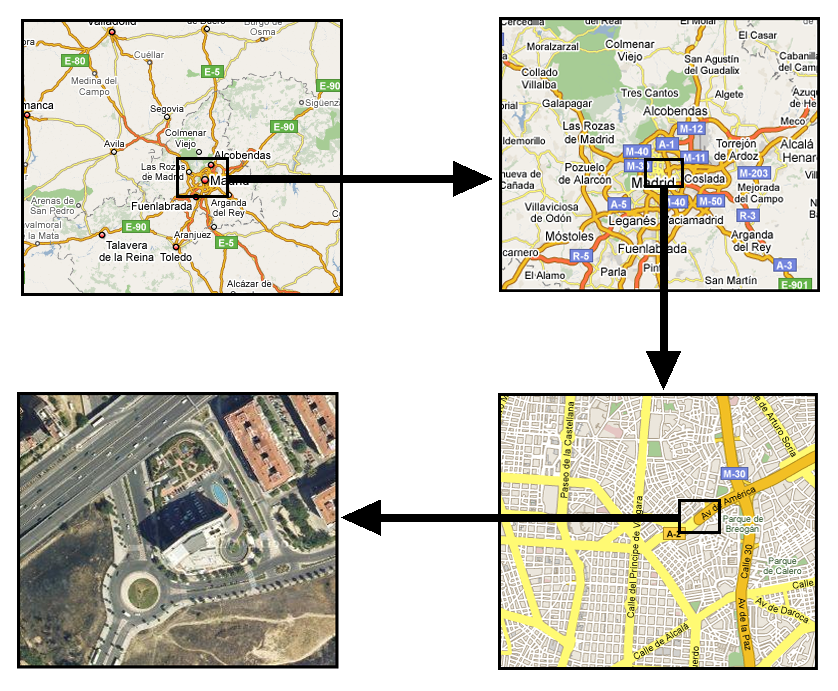
En un SIG es habitual manejar información a diferentes escalas. En función de la escala de representación, la información visualizada será una u otra.

En el caso de imágenes tales como esa fotografía aérea, existen además en un SIG una serie de procesos que también pueden considerarse como parte de la generalización, y que atañen más al rendimiento que a la representación. Para entenderse esto piénsese que las imágenes se componen de elementos denominados píxeles , que son pequeños puntos, cada uno de los cuales tendrá un color asociado (esto lo veremos con mucho más detalle en el capítulo Tipos_datos ). El numero de estos píxeles en una imagen grande es muy superior al de una pantalla (una pantalla también se divide en puntos, si te acercas a una lo podrás ver claramente).

El proceso de representación de la imagen en la pantalla consiste en calcular qué color asignar a cada píxel de la pantalla en función de los de la imagen, pero este proceso, si se utiliza la imagen completa, es muy costoso en términos de cómputo, ya que implica procesar toda la información de la imagen, que puede ser del orden de centenares de millones de píxeles. Si representamos una porción de esa imagen (una porción del territorio que cubre), podemos solo trabajar con los píxeles en esa zona, pero la representación de toda la imagen hace necesario procesar todos los valores que contiene.

Este proceso en realidad puede verse como un tipo de generalización «al vuelo». Ya dijimos que este tenía principalmente dos problemas: el rendimiento y la imposibilidad de obtener resultados óptimos de forma automatizada. En el caso de imágenes, existe el problema del rendimiento, pero es posible automatizar la creación de datos a diferente escala de trabajo. Esto es así debido a que la representación de elementos tales como carreteras o lagos se hace mediante una interpretación de esos objetos, y este proceso es en cierta medida subjetivo, como vimos. En el caso de imágenes no hay que interpretar objeto alguno, ya que esos objetos ya «están representados» en la imagen, y únicamente es necesario disminuir la escala.

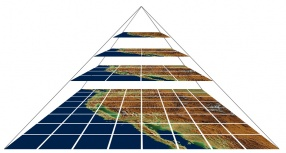
Los algoritmos para llevar a cabo este proceso se conocen como de remuestreo , y los veremos con detalle en el capítulo Algebra_de_mapas . Algunos SIG utilizan estos algoritmos para hacer más fluido el manejo de grandes imágenes mediante la creación de las denominadas pirámides . Cuando el usuario introduce en el SIG una imagen de gran tamaño, este prepara varias versiones de esa imagen a distintas escalas de detalle, de forma que posteriormente pueda recurrir a la que sea más conveniente en cada caso en función de la escala de representación. Es decir, el SIG realiza la «generalización» de esa imagen de forma automática, siendo necesario proporcionarle únicamente la imagen de mayor detalle. La figura \ref{Fig:Piramides} ilustra gráficamente esto.

Pirámides de representación con imágenes preparadas a distintas escalas (Fuente: OSGeo).

Resumen

La cartografía y la geodesia son ciencias que aportan un importante conjunto de conocimientos y elementos al mundo de los SIG, y su estudio es fundamental para cualquier trabajo con un SIG.

La geodesia se encarga de estudiar la forma de la Tierra, con objeto de posteriormente poder localizar de forma precisa los puntos sobre esta mediante un sistema de coordenadas. Dos conceptos básicos en geodesia son el geoide y el elipsoide , superficies de referencia que modelizan la forma de la Tierra. El primero es la superficie formada por los puntos en los que el campo gravitatorio tiene una misma intensidad, y se obtiene prolongando la superficie de los océanos en reposo bajo la superficie terrestre. El segundo es un objeto definido por una ecuación y una serie de parámetros, que permite asimilar la Tierra a una superficie matemática.

El conjunto de un elipsoide y un punto de tangencia con la superficie terrestre (Punto Fundamental), forma un datum .

Para asignar coordenadas a un punto en función de los elementos anteriores es necesario definir un sistema de referencia. Las coordenadas geográficas han sido utilizadas tradicionalmente, y son de utilidad para grandes zonas. Otro tipo de coordenadas más intuitivas son las cartesianas, y para su obtención se requiere el concurso de una proyección cartográfica que convierta coordenadas espaciales en coordenadas planas. Hay muchos tipos de proyecciones, siendo el sistema UTM uno de los más extendidos.

En el ámbito de la cartografía, hemos visto en este capítulo la importancia del concepto de escala, que no pierde su papel fundamental al trabajar en un SIG en lugar de hacerlo con cartografía impresa. Estrechamente relacionada con la escala encontramos la generalización , que comprende una serie de procesos encaminados a la obtención de una representación lo más clara posible de una serie de datos a una escala dada.