Costes, distancias y áreas de influencia
Introducción
Desplazarse entre dos puntos cualesquiera del espacio implica un coste. Cuanto más alejados se encuentren estos, más tiempo llevará efectuar ese desplazamiento y se consumirá más energía, entre otras cosas. La distancia como tal, así como el tiempo o la energía gastada, son ejemplos de variables de coste.
Un coste expresa la resistencia ofrecida por el medio para desplazarse a través de él en un punto concreto.
El análisis de capas que contengan variables de este tipo nos permite calcular los costes globales de desplazarse a lo largo de toda la extensión de la capa, así como evaluar la mejor forma de hacerlo para minimizar dicho coste.
Las variables que podemos utilizar como coste son muy diversas, y este tipo de análisis es de gran utilidad para todos aquellos procesos que impliquen algún tipo de movimiento.
De este modo, el concepto de distancia puede «ampliarse», y con él todas sus implicaciones. Por ejemplo, las zonas de influencia no solo pueden definirse con la mera distancia euclídea, sino en base a otros factores. Así, podemos incorporar el hecho de que, mediando la misma distancia entre una celda y un conjunto de otras dadas, la facilidad de recorrer esta distancia sea diferente, y por tanto no ejerzan todas la misma influencia sobre la primera.
La delimitación de zonas de influencia sobre una base ráster permite no solo introducir estas ideas, sino también aportar más flexibilidad al proceso, pudiendo emplearse parámetros adicionales que condicionen la forma de llevarlo a cabo en cada punto.
Superficies de fricción
Una capa que contiene una variable de coste se conoce como superficie de fricción . Las variables de coste son de tipo cuantitativo y generalmente, aunque no siempre, continuas.
El valor de cada celda de una superficie de fricción indica el coste que supone recorrer dicha celda [ Douglas1994Cartographica ]. Puesto que la celda puede recorrerse en diversas direcciones, se establece que este coste se refiere a hacerlo en la dirección vertical u horizontal, no diagonal. Así, una capa que almacene la variable de coste «distancia» será una capa constante que contendrá en todas las celdas el tamaño de celda $\Delta s$.
No obstante, los costes son, por regla general, variables. Esto es, distintos en cada celda. Veamos algunos casos.
Una capa de pendientes, por ejemplo, es una capa de coste válida, ya que la dificultad de desplazarse sobre el terreno aumenta conforme lo hace la pendiente. De igual modo, el tiempo empleado en atravesar una celda, que será función de diversos factores, también representa un coste.
Una superficie de fricción puede contener también un valor que no exprese directamente un coste, pero esté relacionado con él y permita obtenerlo. Por ejemplo, la velocidad media de tránsito a través de una celda. Con este valor y el tamaño de celda se puede obtener el tiempo de tránsito.
El coste no es necesariamente una variable física de tipo continuo. Por ejemplo, podemos clasificar las distintas zonas de una capa en función de su atractivo visual. Invirtiendo estos valores obtenemos una variable de coste, que nos indica la «dificultad» de atravesar la celda en función de su atractivo. Las zonas con menor belleza suponen un mayor coste. Esto nos puede servir para calcular rutas agradables, ya que las rutas óptimas en este caso son aquellas que pasan por un menor numero de zonas estéticamente no agradables.
Este tipo de variables hacen referencia a los denominados espacios subjetivos [ Gatrell1983Clarendon ], en contraposición a los espacios absolutos sobre los que se registran las medidas de distancia o tiempo que constituyen las fricciones empleadas más frecuentemente.
Aunque la capa con la superficie de fricción cubre toda una extensión dada, es probable que puntos de esta extensión no sean transitables. Si suponemos que el coste viene expresado por la pendiente, hay zonas tales como embalses donde, con independencia de su pendiente, no podemos cruzar. Una solución habitual es asignar a las celdas en estas zonas un valor muy elevado (coste infinito), que haga que no sea viable transitarlas. Una opción más correcta es asignar valor de sin datos a estas zonas, de forma que queden directamente excluidas del cálculo. Esto puede emplearse para excluir en el posterior trazado de rutas óptimas aquellos puntos por los que no se desee transitar, bien sea por los propios valores de la variable de coste o bien por otras razones.
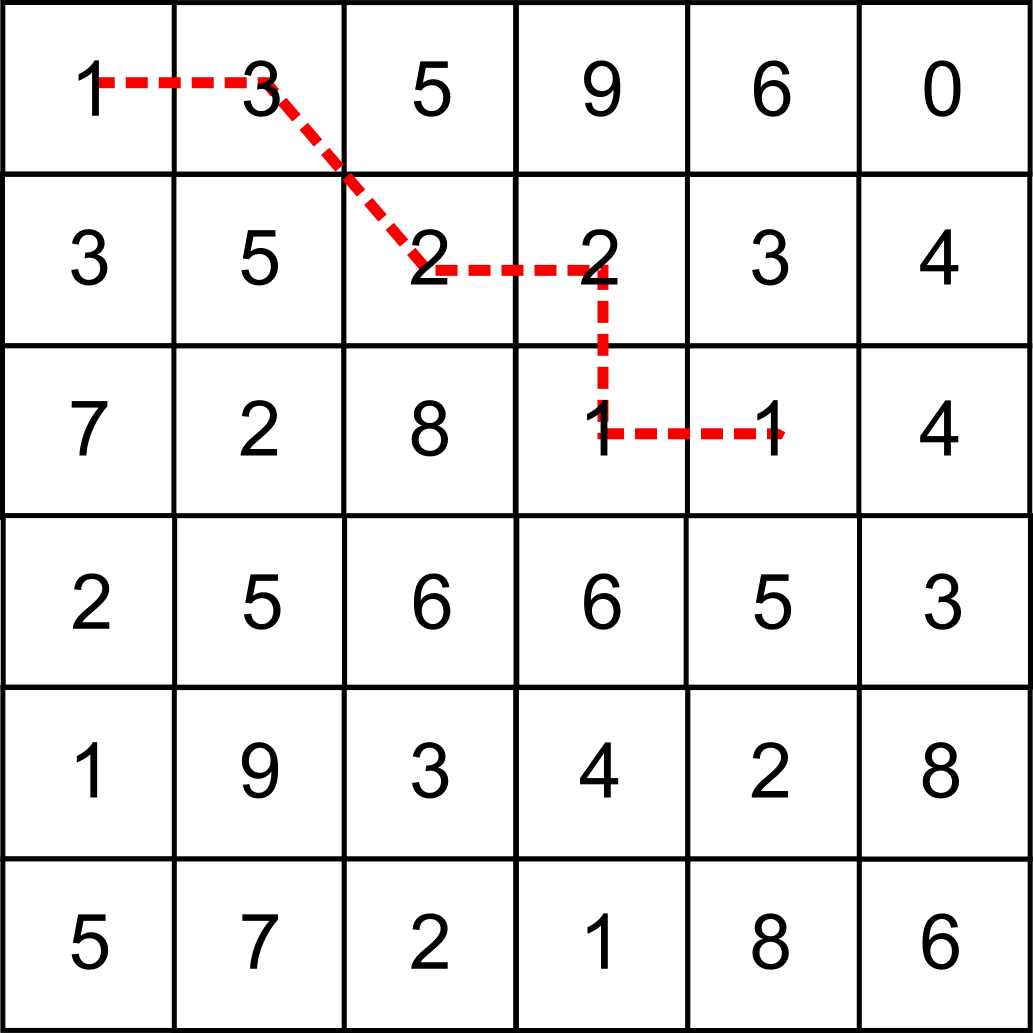
Un ejercicio sencillo para comenzar a trabajar con superficies de fricción es el mostrado en la figura \ref{Fig:Ejemplo_superficie_friccion}. Sobre la pequeña capa ráster de la figura con valores de fricción, se representa una ruta entre dos de sus celdas. Podemos calcular el coste total de recorrer la ruta sumando los costes de cada movimiento entre celdas consecutivas. Para los desplazamientos en dirección horizontal o vertical, el desplazamiento tiene un coste dado por la expresión:
\begin{equation} c = \frac{c_1 + c_2}2 \end{equation}
siendo $c_1$ y $c_2$ las fricciones respectivas de las celdas entre las cuales se produce el desplazamiento.
Si nos movemos en dirección diagonal, el coste que este movimiento supone es
\begin{equation} c = \sqrt{2}\frac{c_1 + c_2}2 \end{equation}
Con lo anterior, el coste de la ruta señalada en la figura \ref{Fig:Ejemplo_superficie_friccion}, comenzando en la celda de la esquina superior izquierda, es igual a
\begin{eqnarray} \frac12 + \frac32 + \frac{3\sqrt{2}}2 + \frac{2\sqrt{2}}2 + \frac22 + \frac22 + \frac22 + \frac12 \end{eqnarray}
Superficies de coste acumulado
Aunque de interés, el análisis anterior es muy simple, y no revela todo el potencial de la superficie de fricción. Mediante un análisis más intenso, podemos, por ejemplo, y dados los mismos puntos, calcular la ruta que haga mínimo el coste total de desplazamiento.
De igual modo, el análisis de la superficie de fricción es la base para resolver otros problemas de rutas óptimas. Dada una serie de puntos posibles de destino y un punto de inicio, podemos calcular cuál es el punto más cercano (cercanía en términos de coste mínimo, no de distancia euclídea), y calcular la ruta óptima y el coste de esta.
Para ello, debemos convertir la capa con los costes unitarios por celda en una capa de coste acumulado . El coste acumulado de cada celda representa el valor del coste total a recorrer desde dicha celda a la celda de destino más cercana, desplazándose por la ruta óptima. Para una superficie de fricción con distancias euclídeas, y un conjunto de $n$ puntos, la capa de coste acumulado correspondiente indica la distancia al punto más cercano. Si utilizamos una superficie de fricción con tiempos de tránsito, la capa de coste acumulado indica el tiempo mínimo que se tardaría en alcanzar uno de esos puntos de destino (el más cercano en términos de tiempo).
De forma habitual, los puntos de destino se recogen en otra capa ráster, codificados con un valor concreto, o bien simplemente con valores cualesquiera y utilizando valores de sin datos en las celdas que no representan puntos de destino.
Para convertir una superficie de fricción en una superficie de coste acumulado en base a unos puntos de destino dados, se sigue el siguiente procedimiento [ Berry1996Wiley ][ Eastman1989Autocarto ] :
- Para cada una de las celdas de destino, analizamos el coste de desplazarse a las adyacentes.
- Si estas no han sido analizadas aún o ya tienen un coste asignado pero es mayor que el calculado en el paso anterior, se les asigna el valor de dicho coste calculado.
- Desde este punto, repetimos el proceso pero en lugar de utilizar las celdas de destino, utilizando todas las celdas que han sido modificadas en la iteración anterior.
- El proceso se detiene cuando no se modifican nuevas celdas, ya que en este punto todas tienen asignado su coste acumulado mínimo.
Para visualizar gráficamente esta metodología, puede observarse que el proceso de ir seleccionando las celdas de análisis de cada iteración se asemeja a la propagación de las ondas al arrojar una piedra en un estanque, a partir de las celdas de destino iniciales que serían como el punto en el que cae la piedra. Contrariamente a lo que puede pensarse, a mayor numero de puntos de destino, menor tiempo de ejecución del algoritmo, de la misma forma que a mayor numero de piedras lanzadas sobre el estanque, menor tiempo tarda toda la superficie del mismo en ser alcanzada por alguna perturbación.
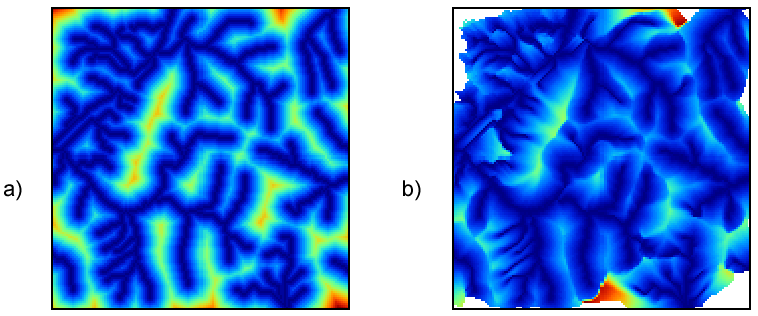
En la figura \ref{Fig:Coste_acumulado} podemos ver la capa de coste acumulado resultante de utilizar tres puntos de destino y una superficie de fricción constante. Puesto que la superficie de fricción es constante, dicho coste acumulado es proporcional a la distancia.
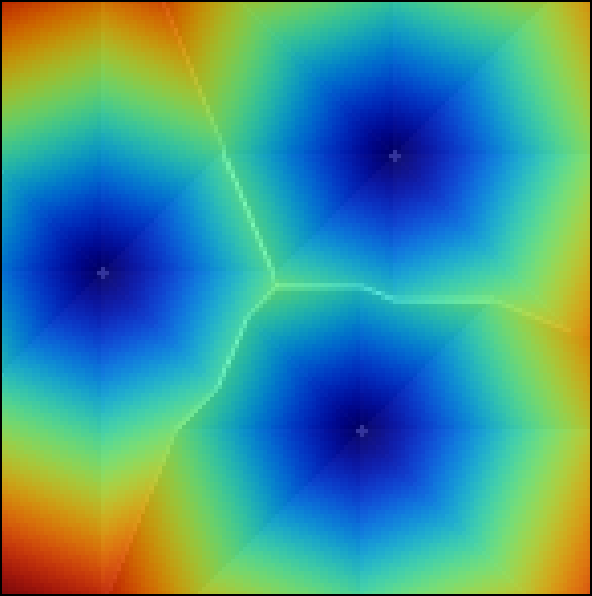
Para calcular la superficie de coste acumulado necesitamos puntos de destino, codificados según algún criterio preestablecido, como ya se ha dicho. Puesto que trabajamos sobre una capa ráster, en realidad debemos definir celdas de destino. Estas, no obstante, no han de representar necesariamente localizaciones puntuales aisladas. Podemos establecer grupos de celdas de destino contiguas, que en realidad representan áreas de destino\ref{Fig:Coste_acumulado_area}. Esto nos permite recoger entidades lineales (por ejemplo, para calculo de costes de desplazamiento a una carretera) o de área, además de, por supuesto, elementos puntuales .
Uno de los problemas principales del cálculo con el método anterior es el debido a la limitación de los ángulos de movimiento. Al igual que veíamos para el modelo D8 de flujo, el hecho de que los movimientos se analicen en la ventana $3\times 3$ obliga a que la dirección sea una de las definidas por las ocho celdas circundantes, es decir, siempre un múltiplo de 45°. Observando la figura \ref{Fig:Coste_acumulado_area}, no es difícil percibir el efecto de esta limitación, del mismo modo que era sencillo detectar visualmente las deficiencias del modelo D8. Este efecto es especialmente patente al emplear una superficie de coste constante, tal y como se ha hecho en la figura anterior.
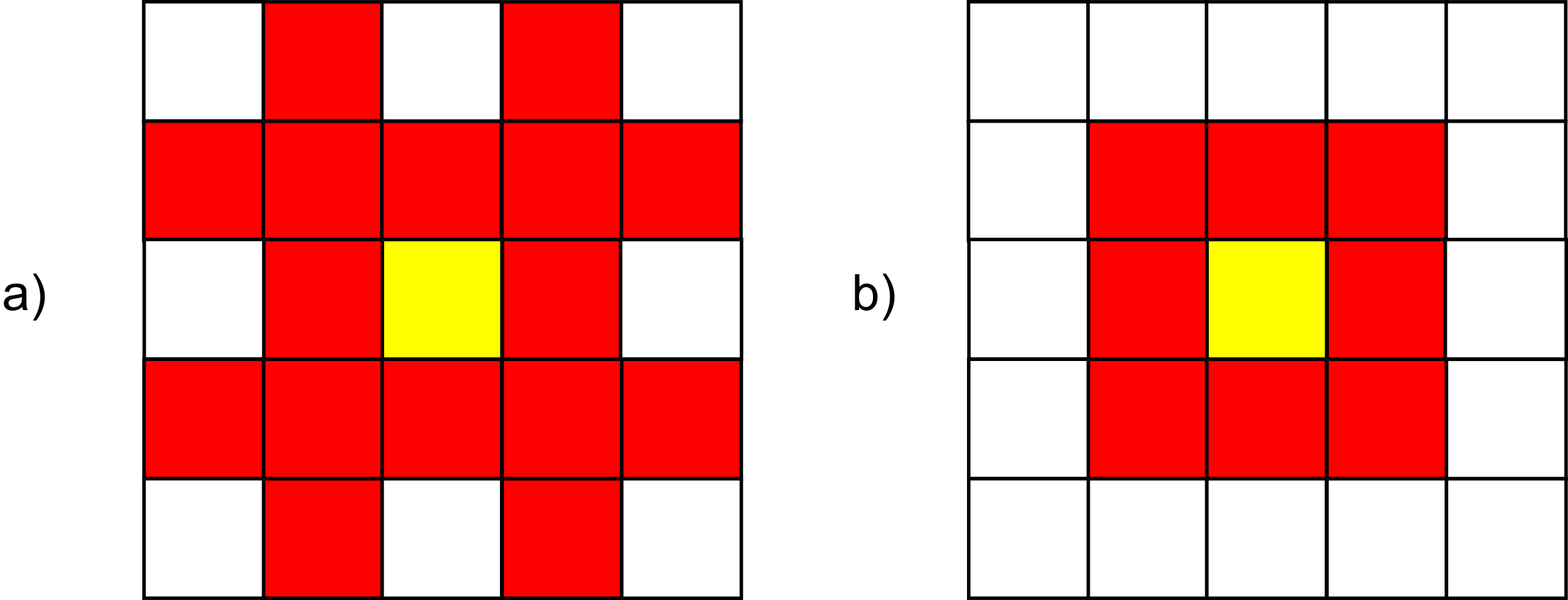
Para solventar en parte este inconveniente, una opción es analizar no solo esas ocho celdas, sino también algunas de la ventana $5\times5$ centrada en la misma celda. En particular, aquellas situadas a salto de caballo desde la celda central, por lo que esta conectividad se conoce como vecindad de caballo , en contraposición a la vecindad de reina que define el conjunto de celdas contiguas en la ventana $3\times3$ [ Chaoqing2003IJGIS ]. La figura \ref{Fig:Tipos_vecindad} muestra esquemas de ambos tipos de vecindad.
Coste isotrópico vs coste anisotrópico
Al introducir el análisis de las superficies de fricción señalábamos la pendiente como una posible variable de coste. Los costes de un desplazamiento dependían de ese valor de la pendiente, así como de la dirección de desplazamiento, para aplicar el factor de corrección $\sqrt{2}s$ en caso de hacerlo diagonalmente. No obstante, además de considerar la dirección de desplazamiento para aplicar esa corrección en función de la distancia entre centros de celda, para modelizar el proceso de forma realista debemos considerarlo junto a la propia naturaleza de la variable de coste. En el caso de la pendiente, resulta obvio que no es igual recorrer la celda ascendiendo por la línea de máxima pendiente que hacerlo por la dirección de la curva de nivel. Es decir, el valor de coste en las celdas de una superficie de fricción no es único, sino que depende de la dirección.
Frente al coste isotrópico (igual en todas las direcciones) que hemos visto hasta el momento, más fácil de modelizar y comprender, encontramos fenómenos en los que la resistencia del medio no es la misma en todas direcciones. Este coste es de tipo anisotrópico. Junto al caso de la pendiente, otro ejemplo claro de esto es, por ejemplo, la resistencia que el viento ofrece al movimiento. Es obvio que el coste de desplazamiento no será el mismo si vamos en contra del viento que si vamos a favor. En general, la mayoría de procesos son de tipo anisotrópico, aunque muchos de ellos pueden simplificarse y estudiarse como procesos isotrópicos.
El concepto de superficie de fricción debe extenderse para acomodar este nuevo tipo de modelos. La capa con valores unitarios no es suficiente, ya que estos reflejan únicamente el coste en una dirección de todas las posibles. La solución habitual es recoger en la superficie de fricción los valores de coste máximo (el que se tendría desplazándose en contra del viento o hacia arriba de la ladera por la línea de máxima pendiente), y acompañar esta de una capa adicional con las direcciones en las que dicho coste máximo se produce. En el caso de la pendiente, esta dirección la podríamos obtener con la orientación en la celda, y en el caso del viento tomando la dirección opuesta a aquella en la que este sopla en cada celda.
Junto a esto, se define una función que, en base a la desviación angular respecto a la dirección de máximo coste, permite calcular los costes unitarios (fricción efectiva) en cualquier dirección. Con estos elementos ya podemos trabajar sobre la capa, estudiar el coste de una ruta concreta entre dos puntos, o crear una capa de coste acumulado de la misma manera que antes lo hacíamos con una capa de coste unitario isotrópico.
Una posible forma para la función anterior es la siguiente:
\begin{equation} c = \frac{c_1 \cos^k(\alpha_1) + c_2\cos^k(\alpha_2)}2 \end{equation}
donde $\alpha_1$ y $\alpha_2$ son las diferencias entre el ángulo en que se produce el movimiento y los ángulos de máximo coste de las celdas, y $k$ una constante.
Pueden adaptarse formulaciones más específicas si se conoce cómo modelizar un tipo de movimiento dado. Por ejemplo, la velocidad de propagación del fuego, conocida la velocidad en la dirección de máxima propagación, puede calcularse para las restantes según ciertas expresiones derivadas del análisis y modelización del fuego.
Dados los focos de un incendio, puede calcularse así el tiempo que tardarán en quemar toda el área definida por la superficie de fricción. En este caso, debe considerarse que los puntos no son de destino, sino de partida, con lo que la dirección a considerar es la opuesta. El trayecto cuyo coste se representa en la capa de coste acumulado no es para dicha celda hasta el foco más cercano, sino desde este.
El caso presentado de la pendiente como factor que condiciona el desplazamiento a pie puede expresarse con más precisión según la siguiente ecuación [ Langmuir1984Scot ]:
\begin{equation} T= a \Delta S + b \Delta H_1 + c \Delta H_2 + d \Delta H_3 \end{equation}
siendo $T$ el tiempo empleado en el recorrido, $\Delta S$ la distancia recorrida, $\Delta H_1$ la distancia vertical recorrida cuesta arriba, $\Delta H_2$ la distancia vertical recorrida cuesta abajo con pendiente moderada y $\Delta H_3$ la distancia vertical recorrida cuesta abajo en pendiente pronunciada. La pendiente moderada va de 5° a 12° y la pronunciada es aquella con ángulo mayor de 12°. Los valores propuestos de las constantes son [ Langmuir1984Scot ] $a=0.72, b= 6.0, c= 1.9998, d= -1.9998$.
Calculando la pendiente existente entre dos celdas entre las que se analice el coste, podemos así estimar el tiempo empleado.
En ocasiones, el movimiento no es posible en todas las direcciones. Es decir, en ciertas direcciones el coste es infinito. Por ejemplo, en el caso de modelizar el movimiento de un flujo aplicando un algoritmo como el D8 como veíamos en Direcciones_flujo . De las ocho celdas hacia las que puede darse el movimiento, solo una de ellas es posible. Las restantes tendrían un coste infinito, pues el movimiento en esa dirección es inviable.
Aplicando este concepto es posible calcular una capa de distancias a un cauce, pero que esta distancia no sea euclídea, sino la seguida por el flujo desde cada punto hasta el punto en el que se unen con dicho cauce. Las celdas de cauce son en este caso las celdas de destino.
La figura \ref{Fig:Distancia_cauce} muestra un mapa de distancia euclídea a un cauce, así como otro de distancia hidrológica, pudiendo apreciarse la diferencia entre ambas.
Si las superficies de fricción son isotrópicas, y son varios los factores que dificultan el desplazamiento, combinar estos es tan sencillo como sumar las capas correspondientes. Si la influencia no es equivalente, pueden normalizarse o bien ponderarse, pero la capa resultante se obtiene con una mera suma y sigue siendo una superficie de fricción isotrópica.
Consideremos ahora el caso de dos variables de coste anisotrópico tales como el viento y la pendiente. En este supuesto no podemos sumarlas, ya que es necesario considerar también las direcciones de coste máximo. Sólo si estas fuesen idénticas podríamos sumarlas y obtener una nueva superficie de fricción, que utilizaríamos con la capa de direcciones de máximo coste de cualquiera de ellas. Este caso es altamente improbable. Incluso puede darse que en un punto el coste máximo de un factor coincida con el mínimo de otro, por ejemplo si el viento sopla pendiente arriba.
El problema estriba en la capa de direcciones, que por contener un parámetro circular tal como se vio al tratar la orientación en Medidas_derivadas_primer_grado , no pueden utilizarse las operaciones aritméticas y estadísticas de la forma habitual. Este caso es similar a lo visto en Estadisticas_lineas .
Al igual que lo visto entonces, la forma de proceder en este caso en considerar el binomio coste--dirección $(c, \beta)$ como un vector y convertirlo en sus componentes en los ejes cartesianos $(x,y)$ según las expresiones
\begin{equation} x = c \cdot \cos{\beta} \qquad ; \qquad y = c \cdot \sin{\beta} \end{equation}
Las componentes de cada variable de coste sobre los ejes $x$ e $y$ ya pueden sumarse para obtener dos capas con la componente del coste total en cada eje. Con estas dos capas puede obtenerse el par de capas resultantes con coste máximo y dirección de máxima fricción, aplicando las expresiones
\begin{equation} c = \sqrt{x^2 + y^2} \qquad ; \qquad \beta = \tan{\frac{y}{x}} \end{equation}
Estas ya pueden utilizarse para obtener superficies de coste acumulado de la forma antes detallada.
Cálculo de rutas óptimas
El valor de cada celda en una capa de coste acumulado nos indica el coste mínimo para alcanzar una de las celdas de destino, pero no nos informa de la ruta que implica dicho coste. No obstante, no es difícil calcular dicha ruta.
Para entender mejor la forma de llevar esto a cabo, resulta de interés representar la capa de coste acumulado con una vista tridimensional, empleando el coste como elevación. Visualizar así esta superficie es una forma muy intuitiva de ver lo que representa y cómo utilizarla. La figura \ref{Fig:Coste_acumulado_3D} muestra la capa de coste acumulado, así como una ruta óptima. Se ve que la superficie contiene tantos sumideros como puntos de destino. Estas son las zonas de mínimo coste (coste cero, ya que son los propios puntos de destino), que aparecen con mínima elevación. La ruta va desde el punto de origen hasta el fondo de uno de dichos sumideros.

La superficie de coste acumulado es en realidad una superficie de potencial, y el desplazamiento entre el punto de origen y el de destino se asemeja mucho, como puede verse en la figura, a la ruta que seguiría un flujo desplazándose hacia aguas abajo si en lugar de coste acumulado fuera elevación el parámetro recogido en la capa. Por tanto, podemos utilizar modelos de dirección similares a los mostrados para el caso del análisis hidrológico ( Direcciones_flujo ). En particular, un modelo sencillo como el D8 en el que el flujo se desplaza hacia la máxima pendiente.
Por la propia forma en la que se construye la superficie de coste acumulado, no existen sumideros aparte de las propias celdas de destino, y siempre existe una celda de menor valor alrededor de cualquier otra, excepto en dichas celdas de destino, que son mínimos absolutos.
Zonas de influencia
Como ya sabemos visto, los objetos geográficos tiene influencia sobre su entorno. Un elemento lineal como un río, o uno puntual como una estación de metro, presentan una funcionalidad o un comportamiento respecto a su entorno que depende de la distancia.
A lo largo de este capítulo hemos visto que la distancia puede interpretarse como un tipo de coste. Por ello, podemos utilizar otras variables de la misma forma que la distancia para definir zonas de influencia.
Al hacerlo, podemos crear zonas de influencia de dimensión fija, tales como las creadas en forma vectorial según vimos en Zona_influencia_vectorial , o, por el contrario, de dimensión variable. Las de dimensión fija pueden tener formas irregulares alrededor del objeto central, ya que esa dimensión ya no es necesariamente en términos de distancia, sino de coste. Cumplen, no obstante, la condición de que todas las celdas en el borde de la zona tiene un mismo valor de coste (del mismo modo que, si empleamos la distancia euclídea, todos los puntos en el límite se encuentran a la misma distancia del objeto central).
En las de dimensión variable, la dimensión de la zona de influencia varía según cada celda de las que conforman el objeto, teniendo cada una una capacidad distinta de ejercer su influencia sobre el medio circundante.
Frente al cálculo de zonas de influencia que vimos para las capas vectoriales, la diferencia estriba en que en este caso no se trata de una operación geométrica, y de que la zona no es «exacta», pues su forma y precisión depende de la resolución de celda.
Zonas de influencia de dimensión fija
Para comenzar, la figura \ref{Fig:Zona_influencia_raster} muestra una comparación entre la zona de influencia calculada sobre el trazado del cauce recogido según un modelo vectorial y la misma zona calculada sobre una base ráster. Para calcular esta última se ha creado la capa de coste acumulado tomando el cauce como conjunto de celdas de destino, pero deteniéndose el algoritmo una vez que se alcanza un umbral de distancia dado. También puede calcularse de la forma habitual, y después reclasificando todas aquellas celdas con distancia mayor que el umbral, para asignarles valor de sin datos.

La primera diferencia apreciable es que la zona de influencia en el caso ráster viene limitada a la capa de entrada en la que se contienen las entidades. En general los SIG operan de este modo, y al efectuar un proceso de álgebra de mapas la salida ráster coincide en dimensiones y tamaño de celda con la entrada. En el caso vectorial no existe restricción espacial alguna, y la zona de influencia puede «crecer» más allá de los límites de la capa de entrada.
Una segunda diferencia la encontramos en el hecho de que, además del límite de la zona de influencia, cuando esta se calcula en formato ráster existe además información en el interior de la misma. Dicha información puede servirnos para cuantificar la influencia existente dentro del área definida. Nótese en este sentido que la influencia es, por regla general, inversamente proporcional al coste, ya que cuanto más costoso sea llegar a una zona desde un punto de destino, menos influencia existirá del uno sobre el otro, así como del otro sobre el uno.
Por otra parte, este mismo proceso lo podemos realizar utilizando otras superficies de fricción, sean isotrópicas o anisotrópicas, sin estar limitados al caso de la distancia euclídea. En el caso vectorial, este cálculo no es posible desarrollarlo, ya que se trata de un proceso meramente geométrico sin el concurso de capas adicionales de fricción. Por ejemplo, la figura \ref{Fig:Zona_influencia_dist_hidro} muestra la misma zona de influencia anterior, con la misma distancia máxima, pero en este caso se trata de una distancia hidrológica en lugar de una euclídea.

Otro ejemplo lo encontramos en la figura \ref{Fig:Zona_influencia_especie}, la cual representa el espacio que se supone ocupado por una determinada especie. A partir de tres puntos donde se ha detectado la presencia de dicha especie, asignando por simplicidad un coste constante a las zonas circundantes en función de su vegetación, y estimando un coste máximo a superar por un individuo de dicha especie en una jornada, se calcula la superficie de coste acumulado y se delimita la zona de influencia. Fuera de esta, es improbable encontrar individuos.
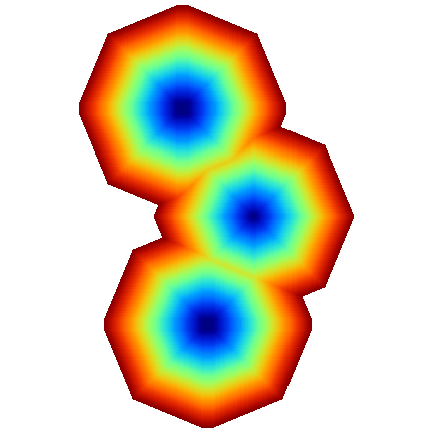
Este análisis puede realizarse de forma similar con datos vectoriales, pero en ese caso se dispone únicamente de dos clases: o el punto esta dentro de la zona de influencia o no. En el caso ráster tenemos una medida de la distancia en cada celda, que sin duda es también una medida de la probabilidad de encontrar un individuo, ya que resulta lógico pensar que en los puntos más cerca del borde la probabilidad es menor que en puntos más centrales.
Pueden calcularse también las zonas de influencia de una manera similar a la vectorial, únicamente delimitando el contorno en función de la distancia euclídea y sin aplicar los conceptos de creación de capas de coste acumulado. En este caso basta tomar todas aquellas celdas que constituyen los objetos centrales (las celdas de destino en el caso del análisis de coste) y marcar con un valor establecido las celdas circundantes a una distancia menor que la distancia de influencia escogida. Se trataría de un análisis focal con una ventana de análisis circular de radio igual a la distancia de influencia, en la que los valores dentro de esta reciben todos el mismo valor. Obviamente, los resultados que pueden obtenerse de este modo son más limitados que aplicando toda la potencia del análisis de costes.
Zonas de influencia de dimensión variable
Al realizar el cálculo de una zona de influencia de dimensión fija, establecemos un umbral de coste acumulado, a partir del cual consideramos que no existe tal influencia. Todos los elementos en el limite del área delimitada tienen el mismo valor de coste acumulado. En ocasiones, no obstante, lo interesante para definir la influencia de un elemento geográfico puede no ser el coste acumulado desde el mismo a las celdas del entorno, sino el propio coste unitario de dichas celdas, o bien otro valor asociado a las mismas, no necesariamente un coste.
Con estos planteamientos podemos definir zonas de influencia de dimensión variable, en las cuales las celdas fronterizas no cumplen ningún requisito relativo al coste acumulado que se da en las mismas.
Para ver un primer ejemplo considérese el siguiente supuesto: se dispone de una carretera y una capa de pendientes. Por la carretera los vehículos circulan sin dificultad, y fuera de ella, los vehículos todo-terreno pueden hacerlo siempre que la pendiente no sea superior al 5%. Tratemos de calcular la zona de influencia de la carretera, es decir, la zona que es accesible con un vehículo todo-terreno.
Podemos abordar el problema como un problema de costes habitual. Tomando la superficie de fricción, reclasificamos todos los valores por encima de nuestro umbral del 5% y les asignamos valor de sin datos para indicar que no son transitables. Despues, calculamos la superficie de coste acumulado, tomando las celdas de carretera como celdas de destino (Figura \ref{Fig:Zona_influencia_vehiculo}). No todas las celdas con pendiente inferior al 5% forman parte del área de influencia, ya que, aunque el vehículo puede transitarlas, algunas no puede alcanzarlas, y quedan como «islas».
El modelo de coste, pese a incluir la pendiente, es en esta ocasión isotrópico, ya que el vehículo no puede desplazarse por zonas con pendiente superior al umbral, con independencia de la dirección en la que lo haga.

Asimismo, no es necesario aplicar ningún umbral a esta capa de coste acumulado, ya que no es ese parámetro el que define la zona de influencia. Si la carretera esta rodeada a ambos lados por zonas completamente llanas, la zona de influencia se extenderá indefinidamente, ya que el coste acumulado no es relevante en este caso. Lo utilizamos simplemente para incorporar la conectividad de las distintas celdas transitables con la vía central. Es por ello que el mapa de la figura \ref{Fig:Zona_influencia_vehiculo} solo marca la zona de influencia sin incorporar los valores interiores de coste acumulado (en este caso pendiente acumulada), ya que no son de interés.
Podemos añadir más complejidad al modelo utilizando un umbral variable. Por ejemplo, sea un cauce del cual conocemos, en cada una de sus celdas el valor de su calado en un evento extremo. El cauce viene definido como una estructura lineal de una única celda de ancho, pero con estos datos vamos a tratar de definir el área realmente ocupada por el agua en ese evento. Esto es, el área de inundación.
Modelizar hidráulicamente un cauce en un supuesto como el presentado es mucho más complejo que lo que vamos a ver, y se requieren más datos, pero podemos plantear una primera aproximación al estudio de ese área de inundación, pues no deja de ser una zona de influencia.
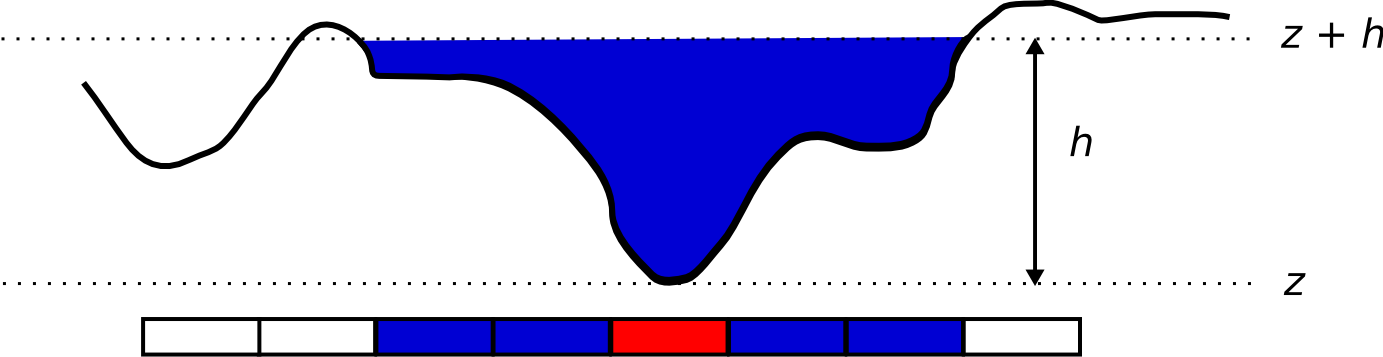
Si en el caso del vehículo teníamos un umbral fijo, ahora este umbral es variable y depende del calado. Como muestra la figura \ref{Fig:Influencia_calado}, para una elevación $z$ en la celda de cauce y un calado $h$, el agua podrá inundar aquellas celdas contiguas con elevación menor que $z+h$. Si tomamos la capa de calado y le sumamos el MDE, tendremos una capa de cauces en las que sus celdas representan los puntos de destino, todas estas celdas tendrán valor de sin datos en la capa resultante, independientemente del valor de elevación que tengan en el MDE.
Por ello, esta nueva capa también nos servirá como capa puntos de destino según la codificación habitual}, y además cada una de ellas contiene el valor de umbral. Es decir, que al operar según se explicó anteriormente para crear la capa de coste acumulado, el umbral dependerá de la celda concreta desde la que nos venimos desplazando. Las celdas por debajo del umbral son viables, mientras que las superiores, no. Este modelo es similar al que planteábamos al analizar la distancia hidrológica, solo que en este caso el umbral que aplicamos no es sobre el coste acumulado, sino que lo usamos para calcular en cada celda los costes unitarios. Para aquellas celdas que superan dicho umbral, el coste es infinito. Para las restantes, nulo.
Influencia acumulada
En los anteriores ejemplos, delimitamos la influencia de un elemento geográfico a un entorno de este, y en algunos casos cuantificamos esta. Si el objeto geográfico se compone de varias celdas, por la propia naturaleza del algoritmo, solo será la más cercana la que tenga influencia en el valor final de coste acumulado de otra celda dada. Esto, que resulta correcto para el cálculo de rutas óptimas, no lo es tanto cuando queremos considerar simultáneamente todas las celdas de destino (o de influencia, según sea el enfoque).
Supongamos que existen núcleos de población cercanos al cauce, cada uno de los cuales tiene una población dada. Si desde estos núcleos la población va hacia el río a practicar la pesca, la influencia de esta actividad sobre cada celda del cauce dependerá de todas las poblaciones cercanas. Dependerá, asimismo, de la distancia o coste de desplazamiento desde las mismas y de la población de estas.
Calcular una capa de coste acumulado utilizando todas las ciudades no sirve en este caso para evaluar su influencia sobre las distintos tramos del cauce. Si tomamos un coste máximo, podemos delimitar una zona de influencia y ver qué zonas del cauce no se ven afectadas. Para las restantes, sin embargo, la influencia es distinta, y la información de que disponemos en esa capa de coste acumulado no refleja la verdadera influencia del conjunto de ciudades. No obstante, los elementos del análisis de costes sí que nos sirven para, aplicándolos de un modo distinto, obtener el resultado buscado.
En Densidad suponíamos que la zona de influencia para el cálculo de densidades era circular, llevando esto implícito que el coste utilizado era la distancia. Ahora conocemos el modo de emplear otras variables de coste y, siendo similar el cálculo de densidades (o probabilidades) al de influencias, podemos proceder de forma similar a lo explicado entonces, operando con las capas de costes asociadas a cada punto de influencia. He aquí la manera de hacerlo:
- Calculamos la superficie de coste acumulado empleando una única ciudad como destino.
- Con la capa anterior, creamos una capa de influencia de dicha ciudad sobre su entorno. La influencia en este caso es inversamente proporcional al coste, así que podemos sencillamente invertir sus valores o aplicar otra función más compleja que relacione ambas variables.
- Repetimos el anterior proceso para cada una de las ciudades. Obtendremos tantas capas de influencia como ciudades existan.
- Sumamos las capas anteriores para obtener la influencia del conjunto de ciudades en cada celda.
- Puesto que estamos estudiando la influencia de la práctica de la pesca, aplicamos una máscara para que la capa anterior quede restringida a las zonas donde esta pueda desarrollarse, es decir, los cauces.
Análisis de redes
Todo el análisis de costes lo hemos realizado hasta este punto sobre una base ráster. Esta es la manera más ventajosa y adecuada de llevarlo a cabo, pues trabajamos con superficies de tipo continuo (las superficies de fricción), que se analizan mejor bajo este modelo de representación.
Un caso particular del análisis de costes es el análisis del movimiento a través de una red, siendo el caso más habitual en un SIG el de una red viaria. El calculo de la ruta de menor coste entre dos nodos de dicha red es un problema típico que tiene numerosas aplicaciones incluso fuera del ámbito geográfico, y constituye una aproximación diferente a la que ya conocemos para el caso ráster.
En el supuesto de un desplazamiento por una red viaria, la división del terreno en unidades regulares que implica el modelo ráster no es adecuada, y resulta mucho más lógico un modelo vectorial que contenga las vías y los emplazamientos entre los que estas se sitúan, recogiendo igualmente la topología de la red. Esta estructura es óptima no solo para el almacenamiento y manejo, sino también para el análisis de costes, como a continuación veremos.
El análisis de costes ráster tal como lo hemos visto permite modelizar los costes a través de vías y el movimiento restringido a estas. Basta excluir las celdas fuera de las vías (asignándoles coste infinito o valores de sin datos) y operar de la forma habitual. No obstante, el hecho de que exista dicha restricción (al analizar un coste de desplazamiento por vías, no podemos abandonar estas), favorece la utilización de un modelo vectorial para estos casos, haciendo que resulte más lógico. Otros elementos de la vía, como el hecho de que algunas de ellas puedan recorrerse únicamente en una dirección, se recogen mejor mediante un modelo de representación vectorial, como ya vimos en el capítulo Tipos_datos al introducir el concepto de topología (de ese capítulo deberías recordar también los conceptos de arco y nodo, que aquí resultan básicos).
Este es el tipo de modelo que implementan, por ejemplo, los navegadores GPS, ya que el movimiento que estudian y sobre el cual nos informan se realiza siempre por una red de carreteras y calles. Sin embargo, si lo que pretendemos es calcular un coste de desplazamiento no confinado a una vía (por ejemplo, para calcular la ruta de menor coste caminando campo a través), es el modelo ráster el que debemos utilizar.
Aunque formalmente son distintos tanto los modelos de representación como los casos particulares de análisis, la implementación de los algoritmos de cálculo de rutas de mínimo coste es en cierta medida similar. Así, los algoritmos sobre una base vectorial comparten elementos con los que ya conocemos para el análisis ráster. Estos algoritmos en realidad derivan todos ellos de la denominada teoría de grafos , una rama de la matemática que se encarga de trabajar con un tipo de estructuras denominadas grafos , de los cuales una red es una caso particular.
El cálculo de rutas óptimas es una de las áreas más trabajadas dentro de la teoría de grafos, y por ello existen muchos algoritmos distintos. El más popular de todos ellos es el conocido como algoritmo de Dijkstra, que es en cierto modo en el que se basan las metodologías que hemos visto para el caso ráster. En realidad, las celdas de una capa ráster pueden entenderse también como una estructura de nodos conectados (una red), con la particularidad de que estas conexiones tienen un carácter sistemático: cada celda (nodo) está conectado siempre a las ocho que se sitúan entorno a ella, y únicamente a estas.
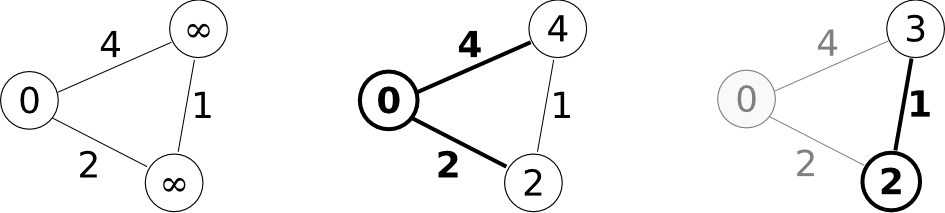
En el algoritmo de Dijkstra, se inicia el cálculo en el nodo de destino y se marcan los nodos a los que este se encuentra conectado, asociándoles el valor de coste entre dicho nodo inicial y cada uno de estos otros nodos. Los restantes nodos, hasta que no sean marcados con un valor concreto de coste, tienen un coste infinito, pues aún no se ha establecido una manera de conectarlos con el nodo de destino.
Al acabar este proceso, se procede a repetirlo, en esta ocasión con todos los puntos que han sido marcados en la iteración anterior. En esta nueva iteración, cada uno de los nodos conectados recibe como nuevo valor de coste el del nodo base (que será uno de los conectados al nodo original) más el coste de desplazarse entre este nodo y el nodo conectado a él. En caso de ya tener un valor de coste asociado, solamente se le asociara este nuevo si es inferior al valor existente (es decir, solo si la ruta que estamos evaluando en este paso es de menor coste que la que anteriormente se evaluó al asignar dicho valor de coste previo). Este proceso de recalculo de coste asociado a un nodo se conoce como relajación .
La figura \ref{Fig:Dijkstra} muestra un ejemplo de un grafo muy sencillo y el proceso de ejecución del algoritmo de Dijkstra sobre este.
La descripción original del algoritmo puede consultarse en [ Dijkstra1959NumMath ]. Para el lector interesado en profundizar sobre esta materia, un buen compendio de algoritmos de cálculo de rutas óptimas puede encontrarse en [ Gallo1988Annals ].
Existen numerosos cálculos relacionados con las redes y la teoría de grafos cuya importancia dentro del ámbito SIG es notable. Uno de los más conocidos es el problema del árbol mínimo de recubrimiento, más habitualmente denotado por su nombre en inglés: minimum spanning tree (MST). Dado un conjunto de puntos, este árbol representa el mínimo conjunto de líneas que permite conectar todos esos puntos. Es decir, el problema del MST implica crear una red que aporte conectividad a un conjunto dado de puntos, teniendo esa red la mínima longitud posible. }
Este problema clásico en la teoría de grafos (y por tanto también muy estudiado al igual que los relativos al cálculo de rutas mínimas que acabamos de ver) tiene numerosas aplicaciones cuando se traslada al campo del análisis geográfico. Por ejemplo, permite calcular la red de canalizaciones necesaria para abastecer a una serie de puntos, minimizando el gasto en tuberías.
La figura \ref{Fig:MST} presenta un ejemplo de uno de estos árboles.
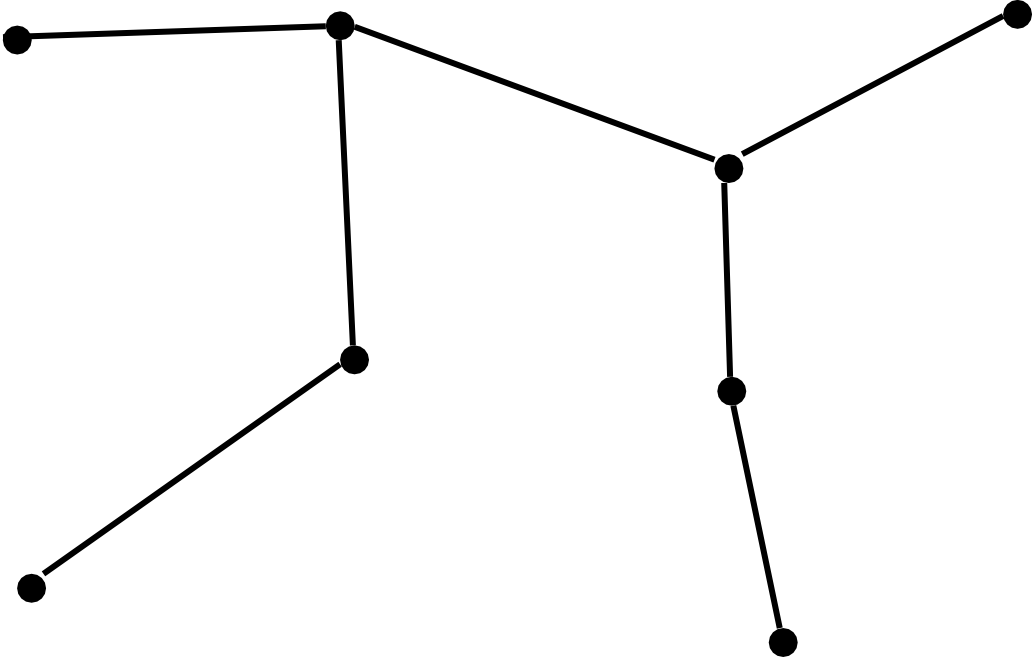
El problema puede resolverse considerando distancia euclídea, o bien teniendo en cuenta que los puntos se encuentran conectados por una red, con un coste dado entre cada par de ellos. En este segundo caso, la obtención del MST implica la reducción de la red original que los conecta, eliminando tramos hasta lograr el conjunto mínimo de ellos que mantiene la conectividad.
De entre los múltiples algoritmos existentes para resolver este problema, los de Prim[ Prim1957Bell ] y Kruskal[ Kruskal1956AMS ] son los más habituales. Los propuestos originalmente por el matemático checo Otakar Boruvka constituyen la base para gran parte de las formulaciones más elaboradas. Pueden encontrarse en [ Nesetril2001DMATH ]
Puesto que se obtiene como resultado un árbol y este es un grafo de tipo acíclico, la ausencia de ciclos (circuitos cerrados) garantiza que no existan tramos «redundantes» en la red. Por esta razón, la estructura de árbol es la adecuada para minimizar la longitud de la red. Desde la perspectiva de su aplicación real, no obstante, un árbol no es la forma más ventajosa de conectar una serie de puntos, ya que la conectividad es reducida y puede perderse si se pierde una de las conexiones (en otras palabras, si se rompe una tubería, habría puntos que no estarían abastecidos, y no resultaría posible abastecerles por otra vía).
Una solución más adecuada es optar por una estructura que trate de reducir la longitud total de la red, pero garantizando una conectividad más robusta. El MST guarda mucha relación con una estructura que ya conocemos, la triangulación de Delaunay, ya que se forma como un subconjunto de las líneas que conforman esta (puede consultarse por ejemplo[ Cheriton1976SIAM ] para ver detalles acerca del algoritmo de cálculo del MST a partir de la triangulación). Si de ese conjunto total de la triangulación se toman las líneas del MST y algunas adicionales, pueden obtenerse estructuras que solucionan de manera óptima el problema de conectar un conjunto de puntos con un diseño de red robusto. Un ejemplo de ésto son las denominadas redes de Gabriel [ Gabriel1969SZ ]. }
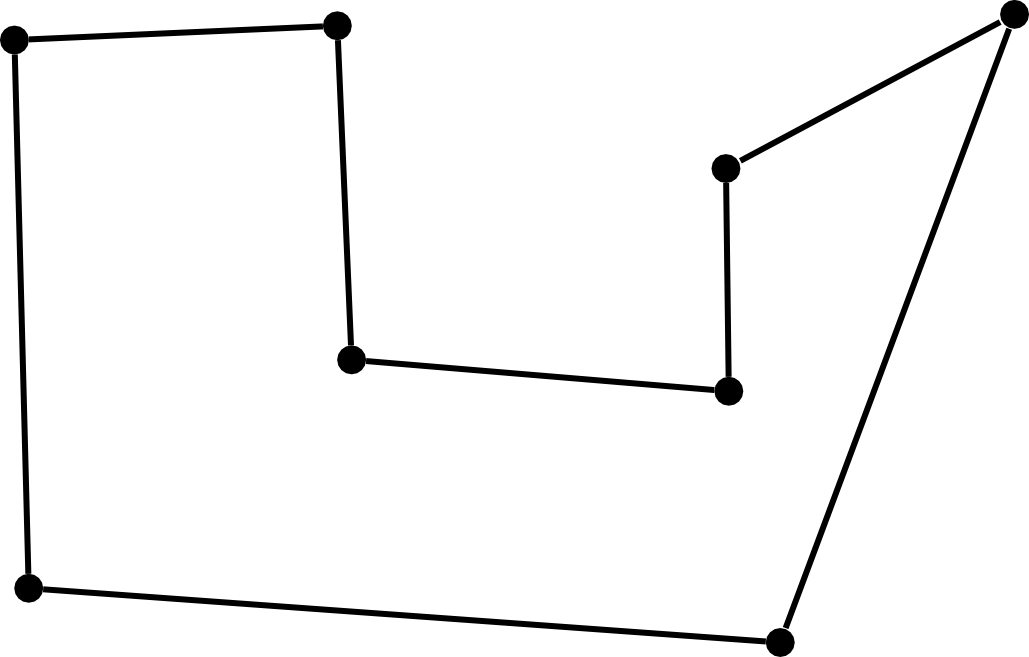
También en cierta forma relacionado con los problemas anteriores, un enunciado clásico con gran aplicación en el ámbito SIG es el conocido como problema del viajante o TSP. Dado un conjunto de puntos, se trata de calcular la forma de visitar todos ellos en un orden dado y regresando al punto inicial, de tal modo que el recorrido total tenga la mínima longitud posible.
La forma más directa y simple de resolver este problema es probar todas las posibles rutas y elegir la más corta. Sin embargo, debido al crecimiento exponencial del número de posibilidades, este planteamiento es inviable, y se ha de optar por métodos de resolución aproximada. Dado el grado de estudio este problema, estas soluciones son muy variadas, y existe bibliografía muy abundante al respecto.
En relación con los SIG y, particularmente, con el tema de este apartado, el problema del viajante cobra interés cuando se considera, al igual que ya veíamos para el MST, que las distancias entre los distintos puntos no han de ser necesariamente euclídeas, sino que pueden ser distancias a través de una red. Así, si una persona ha de visitar un número dado de emplazamientos dentro de una ciudad desplazándose en un automóvil, el orden óptimo en que debe hacerlo es el que se obtendría como solución al problema del viajante para dichas localizaciones, y tomando las distancias entre estas como distancias por las calles de la propia ciudad.
Independientemente de la métrica empleada para calcular la distancia entre puntos, la solución del problema se puede realizar empleando la misma metodología.
En la figura \ref{Fig:TSP} puede verse el circuito óptimo para el conjunto de puntos empleado en el ejemplo anterior de la figura \ref{Fig:MST}.
Para concluir este apartado, comentar que el concepto de buffer vectorial puede extenderse si disponemos de una red sobre la que calcular distancias, haciéndolos más similares a los que hemos visto para el caso ráster, donde la anchura de estos era variable y no se presentaba la característica simetría de los que vimos en el capítulo Operaciones_geometricas . Sobre dicha red, podemos calcular puntos a una distancia dada, y con ellos crear el polígono que delimita la zona de influencia.
La figura \ref{Fig:Buffer_vectorial_red} muestra una red viaria con costes asociados, y una posible zona de influencia basada en dichos costes en lugar de en distancia euclídea.

Resumen
Las superficies de fricción contienen valores de coste que expresan la resistencia que presenta una celda a ser recorrida. Estos costes pueden reflejar muchos distintos factores, siendo la distancia uno de ellos.
Con una superficie de fricción y un conjunto de puntos de destino, se calculan capas de coste acumulado. Empleando estas es posible calcular rutas óptimas que definen la ruta de menor coste desde un punto dado hasta el punto de destino más cercano (en términos de coste).
Con estas ideas, pueden definirse zonas de influencia tanto de dimensión fija como de dimensión variable, y puede estudiarse asimismo la influencia conjunta de una serie de elementos geográficos sobre el entorno inmediato de estos.
Aunque el análisis de costes y superficies de fricción es un análisis con elementos ráster, las redes vectoriales con topología permiten un análisis distinto para calcular rutas óptimas entre puntos de dichas redes.