La calidad de los datos espaciales

Introducción

Puesto que los datos son la base de todo el trabajo que realizamos en un SIG, su calidad es vital para que ese trabajo tenga sentido y aporte unos resultados coherentes y útiles. Siendo la calidad el conjunto de propiedades y de características de un producto o servicio que le confieren su aptitud para satisfacer unas necesidades explícitas e implícitas [ AENOR1995 ], desde el punto de vista del SIG unos datos espaciales de calidad serán aquellos que puedan servir para alcanzar los objetivos de un proyecto concreto, dando sentido a este. En este aspecto, se debe considerar la disposición de los datos per se , aunque también las necesidades a las que pretendemos dar respuesta mediante los datos que utilizamos.

Por definición, ningún dato es perfecto. Todo dato que utilicemos va a contener errores, y estos pueden ser desde totalmente irrelevantes para el desarrollo de un proceso de análisis hasta de tal magnitud que desvirtúen por completo los resultados de dicho análisis. Es importante no solo contar con datos de calidad en los que estos errores sean mínimos, sino conocer el tipo de error que existe en nuestros datos y la magnitud de estos. Saber gestionar el error y ser consciente de las limitaciones de los datos de los que se dispone es importante para saber interpretar los resultados derivados del trabajo con dichos datos.

A lo largo de este capítulo veremos los aspectos más importantes que derivan de considerar el error como parte inevitable de nuestro trabajo con datos espaciales. Ello nos permitirá saber evaluar las capacidades de los datos para servir como punto de partida de nuestro trabajo, y a llevar este a cabo de la mejor manera posible, considerando que se trabaja simultáneamente con un conjunto de datos y con un error implícito asociado a estos.

[ Gomez2004Geofocus ] apunta las siguientes etapas para la modelación del error:

• Identificación de la fuente de error.
• Detección y medida del error.
• Modelación de la propagación del error.
• Propuestas de estrategias para la gestión y reducción del error.

Será sobre estas distintas fases sobre las que trataremos en las próximas secciones.

La importancia de la calidad de los datos

A pesar de su gran importancia, la calidad de los datos espaciales no ha sido una preocupación hasta hace relativamente poco tiempo. Los textos sobre Sistemas de Información Geográfica apenas trataban el tema en sus inicios [ Foote2000 ][ Oort2005NGC ], y solo en la actualidad aparece una concienciación acerca de la importancia que la calidad de los datos espaciales tiene sobre el desarrollo de cualquier trabajo basado en ellos.

Las razones por las que la calidad de los datos empieza a considerarse como un elemento de gran relevancia en el ámbito geográfico son principalmente dos [ Oort2005NGC ]:

• Aparición de los SIG.
• Amplio crecimiento del volumen de datos espaciales disponibles, especialmente los derivados de satélites.

Estos dos factores, inevitablemente unidos, han favorecido que el volumen de trabajo sobre datos espaciales sea mayor y que además se use un número más elevado de datos distintos. Es lógico pensar que, a raíz de esto, haya surgido el interés por evaluar y tratar de forma rigurosa las condiciones en las que estos trabajos se están llevando a cabo.

La preocupación por la calidad de los datos es básica por el simple hecho de que datos de mala calidad generan inevitablemente resultados de mala calidad. Utilizar un dato de mala calidad es equivalente a utilizar un modelo equivocado. Si el modelo no es cierto, no importa la buena calidad de los datos, ya que los resultados que arrojará tampoco lo serán. Del mismo modo, un dato con un error superior al que puede resultar tolerable para una determinada tarea hace que la calidad de este sea insuficiente, y los resultados obtenidos carecen de valor.

A pesar de que la aparición de los SIG ha sido una de las razones principales para que se tenga en consideración la calidad de los datos y se especifique formalmente el modo de tratarla y gestionarla, los SIG en sí no disponen apenas de herramientas para asistir en estas tareas. Aunque la ciencia de la información geográfica ha avanzado mucho en ese sentido, y el conocimiento relativo a la calidad de los datos espaciales es mucho mayor, los SIG no han incorporado ese conocimiento y carecen de funcionalidades al respecto. Dicho de otro modo, existen las formulaciones y los elementos teóricos, pero estos aún no se han visto materializados (o lo han hecho de forma prácticamente anecdótica) en los SIG de uso habitual. Por esta razón, la mayoría de usuarios de SIG no tienen en cuenta rigurosa y formalmente la calidad de los datos a la hora de desarrollar su trabajo, quedando aún mucho por avanzar en este sentido.

Un elemento clave para el control de la calidad es la existencia de metadatos, que informan acerca de dichos datos sobre una serie de aspectos relativos a estos, entre ellos aquellos que afectan a la calidad. Los metadatos se tratan con gran profundidad dentro de este libro en el capítulo Metadatos .

Conceptos y definiciones sobre calidad de datos

Antes de entrar en el estudio directo de la calidad de los datos espaciales y el estudio de los errores que pueden presentarse en un dato espacial, es necesario definir algunos conceptos básicos y alguna terminología al respecto.

El concepto básico es el error , que no es sino la discrepancia existente entre el valor real (puede ser un valor de posición, de un atributo, o cualquier otro), y el valor recogido en una capa. El error puede ser de dos tipos: sistemático o aleatorio .

Dos términos importantes en el estudio de la calidad son la precisión y exactitud . La precisión indica el nivel de detalle con el que se recoge la información. Una capa en la que las posiciones se han medido con 5 valores decimales es más precisa que una en la que se han medido con un único decimal.

$$\label{Fig:Imprecision_exactitud}$$

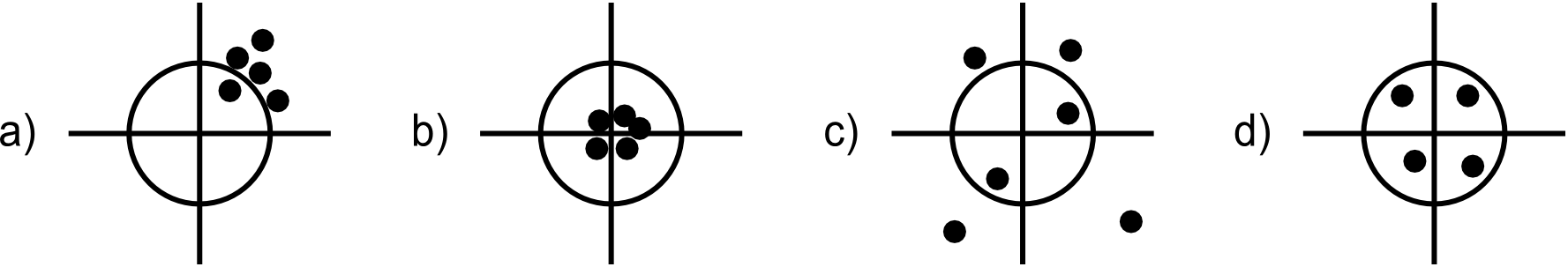
Dependiendo del uso que se pretenda dar a una capa de datos geográficos, se requerirá una u otra precisión. Un trabajo geodésico requerirá medir la localización de un punto con precisión milimétrica, mientras que para un muestreo para inventario forestal es suficiente localizar las parcelas correspondientes con una precisión mucho menor.

Por su parte, la exactitud nos indica el grado en que los valores estimados se asemejan al valor real.

La exactitud se calcula con el error sistemático, mientras que la precisión se calcula a partir del error aleatorio. Existe una relación directa entre precisión y exactitud, y en ocasiones se emplean ambos términos indistintamente. Si no existen errores sistemáticos (no existe un sesgo), la precisión y la exactitud son iguales.

Es posible, no obstante, que un dato sea muy preciso pero poco exacto, ya que las magnitudes de los distintos tipos de errores pueden ser muy distintas. Este hecho puede verse claramente en la figura \ref{Fig:Imprecision_exactitud}.

Por último, un parámetro relativo al error es la incertidumbre . Habitualmente, el valor real es desconocido, por lo que el error no puede conocerse. La incertidumbre refleja la medida en que no podemos tener certeza de la validez de nuestros datos. La incertidumbre es un concepto más amplio que el error, y auna tres componentes [ Fisher1999Wiley ]:

• Error
• Vaguedad . Aparece como consecuencia de definiciones pobres o incompletas, así como cuando los objetos que se modelizan en los datos no presentan límites bien definidos. Por ejemplo, en una capa de clases de vegetación, la transición entre una clase y otra se produce normalmente de forma gradual, por lo que establecer una frontera brusca es un hecho artificial que aumenta la incertidumbre, y el significado de asignar un punto en concreto a una clase dada es más vago cuanto más cerca de esa frontera nos encontramos.
• Ambigüedad . Cuando no existen definiciones inequívocas de los conceptos fundamentales, aparecen ambigüedades que añaden igualmente incertidumbre al dato creado en función de estos.

Tradicionalmente se ha trabajado con el error y no con el concepto de incertidumbre, pero conocer esta es igualmente importante a la hora de evaluar la calidad de los datos, y la modelización de la incertidumbre es una alternativa a la modelización del error.

Fuentes y tipos de errores

Cuando un dato espacial llega a nosotros para ser empleado en un SIG, ha pasado por una serie de etapas a lo largo de los cuales puede haber incorporado errores. Estudiando esas etapas por separado, encontramos las siguientes fuentes de error [ Heuvelink1998Taylor ][ Heywood1998Longman ]:

• Errores de concepto y modelo . Al recoger la información espacial utilizamos algún modelo de representación (ráster, vectorial), el cual siempre tiene alguna deficiencia. La realidad y las tareas que pretendemos realizar con una capa de información espacial no se adaptan por completo a ninguno de los modelos de representación, y el hecho de optar por uno u otro conlleva la introducción de algún error, o condiciona para la aparición de unos u otros errores en las etapas posteriores.
• Errores en las fuentes primarias . El dato vectorial del que disponemos proviene originariamente de una fuente primaria, la cual puede contener errores. Si esta fuente contiene errores, estos aparecerán también en los datos que se deriven de este. Así, si digitalizamos en base a un mapa escaneado y la hoja original es errónea, también lo serán las capas que creemos en esa digitalización.
• Errores en los procesos de creación de la capa . Los procesos que realizamos para crear la capa pueden incorporar errores en el resultado. Por ejemplo, en el proceso de digitalización en base a ese mapa escaneado pueden aparecer errores por razones tales como un mal trabajo del operario, ya sea al digitalizar las entidades sobre una tableta o al teclear los valores de los atributos. Otros procesos, como pueden ser los de conversión entre los modelos ráster y vectorial, también pueden tener como consecuencia la aparición de errores. Los capítulos Creacion_capas_raster y Creacion_capas_vectoriales tratan estos procesos de conversión, y se verán en su momento los posibles errores que pueden aparecer en cada caso y las razones por las que lo hacen. Igualmente, se verá cómo aplicar a esos procesos los elementos de medida del error que se desarrollarán más adelante en este capítulo.
• Errores en los procesos de análisis . Un dato espacial puede derivar de un proceso de análisis, y en él pueden aparecer errores debidos principalmente a dos razones: o bien la capa original objeto de análisis contiene de por sí errores, o bien el proceso no es por completo correcto. Veremos en el capítulo Geomorfometria cómo a partir de un MDE podemos calcular una capa con valores de pendiente, y cómo existen varios algoritmos distintos para realizar este cálculo. Ninguno de esos algoritmos es completamente preciso, y los valores calculados presentaran discrepancias de distinta magnitud con el valor real de pendiente, en función de diversos factores.

  Por su parte, el propio MDE también tiene sus errores, y estos se propagan a los resultados que derivamos de él, como veremos más adelante con detalle.

  En la parte dedicada al análisis veremos muchas operaciones que van a generar nuevos datos espaciales, y que pueden implicar la aparición de errores. Trataremos estos en su momento en la medida que ello pueda ser relevante para el manejo y utilización de esos datos derivados.

Las componentes de la calidad

La calidad de un dato espacial depende de muchos factores. Las características que dotan de dicha calidad al dato espacial son variadas, pues el dato espacial es en sí complejo, y cada una de estas características es susceptible de incorporar errores y por tanto de implicar una pérdida de calidad por ello. Los siguientes son algunos de los componentes principales de la calidad del dato espacial [ Oort2005NGC ]:

• Exactitud posicional . Todo dato espacial tiene asociada una referencia geográfica. La precisión con la que se toma esta condiciona la calidad del dato.

  Esta precisión puede considerarse únicamente en los ejes $x$ e $y$, o también en el eje $z$ (elevación). Esta última, no obstante, puede considerarse como un atributo si se trabaja en un SIG bidimensional, y tratarse de la misma forma que cualquier otra variable de similar índole sin significado espacial, tal como la temperatura en el punto ($x,y)$ en cuestión.

• Exactitud en los atributos . Si la componente espacial puede tener errores, estos también pueden aparecer en la componente temática. Los valores asociados a una coordenada u objeto espacial pueden haber sido medidos con más o menos exactitud, o presentar valores incorrectos por muy diversas causas.

  Cuando el atributo en cuestión es de tipo categórico, puede existir un error de clasificación (se asocia la entidad espacial a una categoría errónea), mientras que en el caso de atributos no categóricos pueden sencillamente aparecer valores mayores o menores que los reales.

• Consistencia lógica y coherencia topológica . Los datos espaciales no son elementos independientes, sino que existen relaciones entre ellos. Un dato de calidad debe recoger fielmente estas relaciones, siendo la topología la encargada de reflejar este tipo de información. Por ello, debe existir una coherencia topológica en el dato espacial.

  Además de la coherencia de las relaciones, existe una coherencia implícita en todo atributo o valor recogido, de forma que resulte lógico. Estos atributos y valores han de ser coherentes con las escalas de medida o el tipo de valor que se espera, entre otros. Así, un valor de elevación no puede ser igual a «suelo calizo», ni un valor de temperatura expresado en Kelvin igual a -87.

• Compleción . El dato espacial no recoge todo lo que existe en una zona dada. Algunos elementos pueden no haberse recogido por cuestiones de escala (menores de un tamaño mínimo), pero también pueden incluirse o excluirse en función de otros criterios, en especial para el caso de mapas temáticos. Estos criterios deben conocerse para saber por qué un dato espacial contiene una serie de valores o elementos y no otros.
• Calidad temporal . Aunque los datos espaciales son «imágenes» estáticas de la realidad, el tiempo es importante en muchos sentidos, pues afecta directamente a su calidad. La realidad que representa un dato geográfico es una realidad que varía con el paso del tiempo, y por tanto este paso del tiempo puede degradar la calidad del dato espacial en mayor o menor medida.
• Procedencia . Un dato espacial puede provenir de una fuente más o menos fiable, o haber sido generado a través de uno o varios procesos, en cada uno de los cuales se puede haber introducido algún tipo de error. Conocer la procedencia de un dato y los procesos que se han empleado en su confección es necesario para poder evaluar su calidad.

Es importante recalcar que los errores que pueden incorporarse en estas componentes de la calidad pueden ser tanto de tipo cuantitativo como de tipo cualitativo, y que ello no está necesariamente ligado a la naturaleza de la componente o el tipo de variable a la que esta hace referencia. Así, un error en un atributo de tipo categórico supone un error cualitativo, pero un error posicional en la componente $z$ (o de atributo de tipo continuo, si lo consideramos como tal) también puede dar lugar a un error cualitativo, como se muestra en la figura \ref{Fig:Error_cualitativo_elevacion}.

$$\label{Fig:Error_cualitativo_elevacion}$$

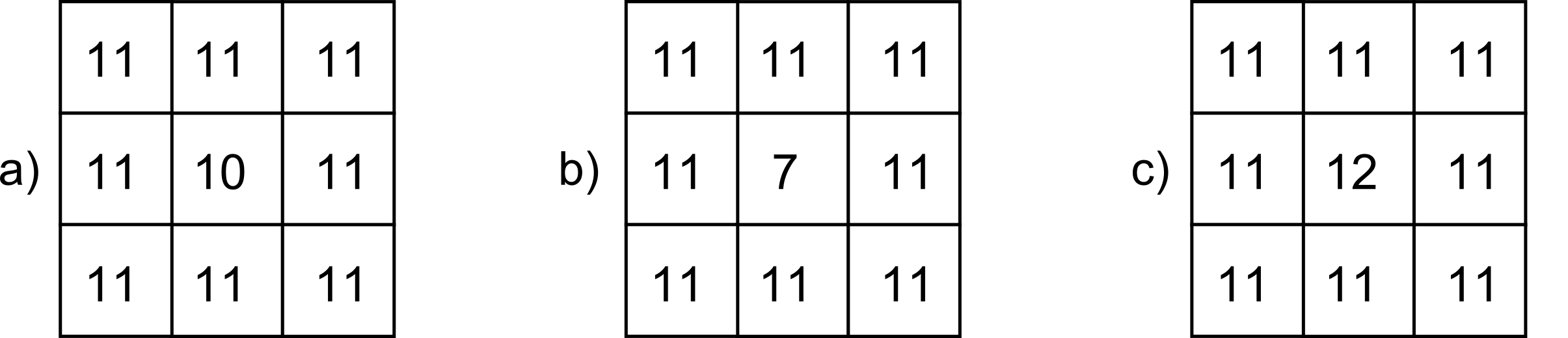
En la figura, que representa una porción de un Modelo Digital de Elevaciones y dos variantes alternativas con sendos errores de medición de la elevación, en el primer caso, y pese a que el error es mayor (hay mayor discrepancia entre el valor real y el recogido en el MDE), no varía la configuración del terreno. En la celda central encontramos una depresión, ya que en ella la elevación es menor que en las circundantes, y esto sigue ocurriendo así a pesar de existir ese error posicional. En el segundo caso (subfigura c), sin embargo, el error es menor en magnitud, pero al ser de signo contrario hace que la depresión se convierta en un pico, una configuración del terreno exactamente inversa. Si estudiamos las formas del terreno en ese punto (un análisis que arroja resultados cualitativos), obtendremos un valor erróneo.

Veremos más adelante que este tipo de errores son de gran importancia para muchos análisis, en particular para los relacionados con el comportamiento hidrológico del terreno, que estudiaremos en el capítulo Geomorfometria .

La forma en que los distintos tipos de errores aparecen en una capa es diferente en función del modelo de representación empleado, ya que cada uno de estos modelos tiene sus propias debilidades, y las fuentes de datos de las que pueden proceder son asimismo distintas.

Así, los errores posicionales son más comunes en el caso de capas vectoriales, y una de las fuentes de error principal en este sentido son los procesos de digitalización, especialmente si son de tipo manual. Junto a los errores que vimos en el capítulo Fuentes_datos (véase Condiciones_digitalizacion ), existen otros que pueden aparecer al crear una capa vectorial, tales como los que se muestran en la figura \ref{Fig:Errores_digitalizacion} para el caso de digitalizar una línea.

$$\label{Fig:Errores_digitalizacion}$$

Con independencia de la pericia y experiencia de un operador, resulta imposible que sea capaz de reproducir exactamente el objeto original y trazar con el cursor de la tableta digitalizadora o el ratón todos los detalles de este con absoluta fidelidad. Entre los errores que pueden aparecer encontramos falsos nudos (intersecciones de una línea consigo misma que no existen en realidad), puntos situados fuera del objeto, coincidencia imperfecta entre polígonos o mala referenciación de la hoja al situarla sobre la tableta (en el proceso de registro).

El problema principal en el caso de digitalizar líneas o polígonos (que pueden causar la aparición de mayor número de errores por su mayor complejidad) estriba en que aquello que se digitaliza es un conjunto infinito de puntos, y el proceso de digitalización solo puede recoger un número finito de ellos y después unirlos mediante segmentos rectilíneos.

La componente temática de una capa vectorial también puede adolecer de errores, que derivan a su vez tanto del proceso de introducción de los mismos como de los procesos de medición mediante los que se ha obtenido el valor concreto.

En el caso de capas ráster, la introducción de la componente temática no se realiza hacerse manualmente con el teclado, como sí puede sucede con las capas vectoriales. Ello no significa que las capas ráster no presenten errores en sus valores, pero el origen de estos es diferente. Un error habitual aparece en capas con información categórica que proceden de la clasificación de imágenes aéreas o de satélite. Los procesos que clasifican cada píxel de la imagen en función de sus Niveles Digitales (los cuales veremos en el capítulo Estadistica_avanzada ) introducen frecuentemente errores, y aparecen píxeles mal clasificados cuyo valor de clase no es correcto.

Los errores posicionales en las capas ráster se presentan de forma distinta a lo mostrado en la figura \ref{Fig:Errores_digitalizacion}. Las entidades tales como líneas van a tener una representación errónea debido a la resolución de la capa ráster, que no va a permitir registrar con fidelidad su forma real. Por otra parte, la georreferenciación de una imagen incorpora asimismo errores, que son equivalentes al error de registro en la digitalización vectorial. Este error va a ser distinto según las zonas de la imagen, ya que la distorsión que implica la transformación realizada no supone un error constante. Veremos estas funciones con más detalle también en el capítulo Procesado_imagenes , donde se tratan los dos principales errores que afectan a las imágenes: errores geométricos y errores radiométricos (básicamente, errores posicionales y errores en los Niveles Digitales).

Además de los errores de un único dato espacial (una capa de información), es importante considerar la forma en que los errores de distintos datos interactúan entre sí. En el trabajo con SIG es raro emplear una única capa, y lo más frecuente es trabajar con varias de ellas coordinadamente, cada una con sus respectivos errores. El modo en que esos errores se afectan entre sí puede condicionar la calidad de los resultados de forma similar a como los propios errores como tales lo hacen.

Como muestra la figura \ref{Fig:Sinergia_errores}, dos errores sistemáticos de igual magnitud en sendas capas pueden tener efectos distintos sobre el resultado dependiendo de sus signos.

$$\label{Fig:Sinergia_errores}$$

En la figura, tanto la capa de puntos como la de polígonos presentan un error sistemático. No obstante, un análisis que cuente el número de puntos dentro del polígono seguirá dando el mismo resultado en uno de los casos, ya que la forma de los errores de ambas capas hace que estos no afecten a este análisis, mientras que en el otro caso el resultado es completamente distinto del real.

Detección y medición de errores

Ahora que conocemos las fuentes y tipos de error, la evaluación y tratamiento de este empieza por su localización para saber a qué elementos del dato espacial afecta. Existen diversas metodologías para «inspeccionar» un dato espacial en busca de errores, que van desde métodos sencillos y obvios hasta avanzadas técnicas con base estadística para detectar patrones particulares o elementos «sospechosos» de contener algún error.

La forma más sencilla es la mera exploración visual. Algunos errores resultan obvios y una inspección sencilla permitirá localizarlos sin dificultad. Una coincidencia deficiente entre polígonos dejará un espacio en blanco que, si es de tamaño suficiente, puede ser localizado sencillamente en una exploración visual. De igual modo sucede con otro tipo de errores, en particular los errores de posición tales como los falsos nudos o la aparición de formas «ilógicas» (calles con ángulos muy bruscos, por ejemplo).

Es importante en este sentido que la representación del dato espacial sobre la que se realiza la exploración visual sea clara y adecuada, para revelar de la forma más notoria posible las posibles deficiencias de este. En este libro se dedica una parte entera a la visualización y representación de la información espacial y, al contrario de lo que pueda pensarse, esta no es solo de importancia para la generación de resultados al final de un flujo de trabajo, sino desde su mismo inicio. El análisis visual de los datos de partida, así como otros procesos de análisis, pueden beneficiarse de una representación correcta.

Existen errores que pueden detectarse visualmente, pero cuya detección (y corrección) puede automatizarse. Errores de este tipo son, por ejemplo, las conexiones imprecisas entre segmentos, que ya vimos en el capítulo Fuentes_datos . La función de snapping (ajuste por tolerancias), que se utiliza a la hora de digitalizar una capa vectorial, puede aplicarse a posteriori , una vez que la capa ya ha sido digitalizada. El SIG puede buscar esos enlaces imperfectos y convertirlos en enlaces correctos, resolviendo las uniones en las que exista una distancia entre vértices menor que una tolerancia preestablecida.

Como sabemos, hay SIG que son capaces de manejar topología y otros que no. También hay formatos de archivo que pueden almacenar topología y otros que no están pensados para ello. Por esta razón, los SIG topológicos trabajan a menudo con datos sin topología, pero a partir de los cuales puede crearse esta, e implementan por ello las funciones para dicha creación de topología. Esta creación implica la corrección de errores topológicos que puedan existir en los datos originales, que no son relevantes en el caso de no trabajar con topología, y por ello pueden no haber sido detectados o eliminados. Errores como las antedichas falsas conexiones o los polígonos con adyacencia imperfecta, ambos se pueden corregir de forma automática, formando parte esas funciones de corrección de las rutinas de creación de topología.

Otros errores no pueden detectarse visualmente, en muchos casos porque los motivos del error no se representan y no aparecen en la visualización. Errores topológicos relativos a las estructuras de datos empleadas para recoger dicha topología entran en este grupo. En muchos casos, pueden no obstante corregirse de forma automática a través de operaciones de filtrado y limpieza , que se encargan de controlar la coherencia topológica del dato.

En el terreno de los atributos, la detección de errores puede llevarse a cabo empleando las técnicas estadísticas habituales. La detección de valores improbables ( outliers ) es uno de los procesos básicos. Estos outliers son observaciones dentro de un conjunto de datos que no parecen guardar consistencia con el resto del conjunto [ Barnett1995Wiley ] y cuya detección puede llevarse a cabo de modo analítico o bien de modo visual, representando gráficamente los valores de los atributos. En general, las metodologías se fundamentan en comparar los valores con una distribución teórica y detectar la discordancia con esa distribución. Formas automatizadas de detectar outliers pueden encontrarse en [ LastOutliers ].

Observaciones de este tipo, alejadas de las características generales del conjunto de datos, pueden derivar de medidas erróneas tales como las provocadas por un equipo de medición en mal estado, aunque también pueden representar valores correctos pero de carácter excepcional.

Si se combina la componente espacial con la componente temática encontramos otro tipo de valores inusuales, los denominados outliers espaciales . Estos se definen como observaciones que son discordantes con las observaciones realizadas en su vecindad, y que expresa la idea lógica de que las mediciones cercanas deben tener valores similares} [ Lu2003IEEE ].

La diferencia entre un outlier en la componente temática y un outlier espacial es clara. Así, un valor de 10000 metros en elevación constituye siempre un valor excepcional, ya que va a encontrarse lejos de los valores medios recogidos, independientemente del lugar donde se hayan efectuado las mediciones. Un valor de 5000 metros puede constituir un outlier espacial en unas zonas (si tomamos medidas de elevación en, por ejemplo, Madrid, ya que será muy distinto del resto de elevaciones), pero puede ser un valor perfectamente lógico en otras zonas de estudio.

La detección de este tipo de valores puede realizarse, al igual que en el caso no espacial, de forma analítica o bien mediante exploración visual.

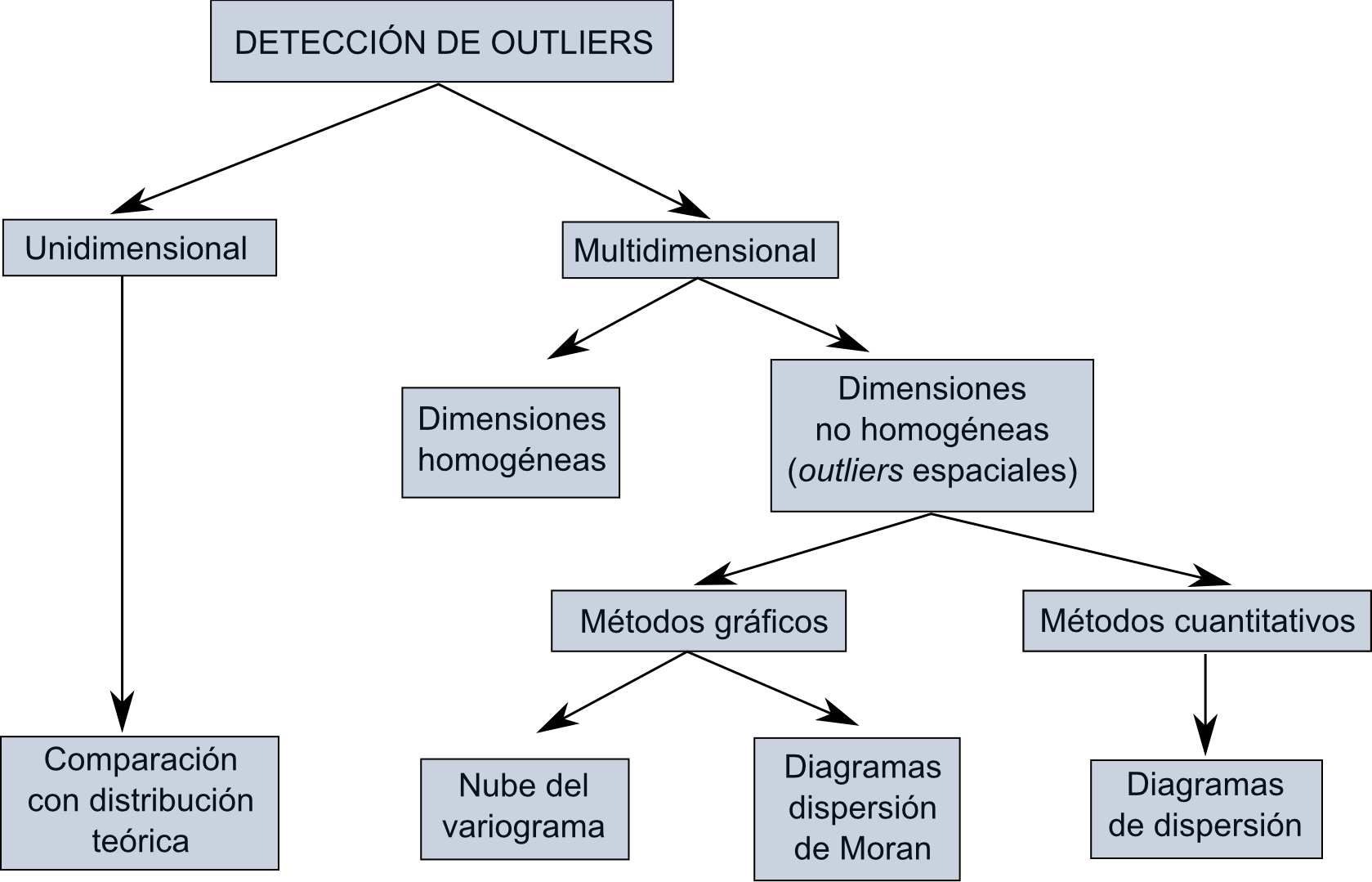
En base a lo anterior, existen una serie de procedimientos y metodologías para la detección de valores ilógicos en un conjunto de datos, los cuales se dividen de forma más genérica en dos grupos principales: unidimensionales y multidimensionales. Cuando en los multidimensionales la vecindad se define únicamente en función de la localización espacial y sin utilizar la componente temática, se tiene la detección de outliers espaciales. La figura \ref{Fig:Deteccion_outliers} muestra un esquema de esta clasificación y las metodologías más habituales. En [ Shekhard2003Unified ] puede encontrarse más información al respecto.

$$\label{Fig:Deteccion_outliers}$$

Una vez localizado el error, este puede cuantificarse de diversas formas, según sea la naturaleza de la variable sobre la que se produce dicho error.

Los errores posicionales o los atributos no categóricos son variables de tipo cuantitativo. El Error Medio Cuadrático es la forma más habitual de medir esos errores. Su expresión es:

\begin{equation} \mathrm{EMC}= \sqrt{\sum_{i=1}^N{\frac{(y_i - y_i')^2}{N}}} \end{equation}

donde $N$ es el total de puntos en los que se comprueba el error, $y$ el valor real, e $y'$ el valor estimado. En esencia, se trata de una desviación típica, por lo cual se asume al emplear esta medida que los errores son aleatorios y se distribuyen normalmente.

Otras medidas utilizadas son el Error Medio , el Error Medio Absoluto o el Error Máximo .

Para valores cualitativos no puede aplicarse esta medida, y deben emplearse otros parámetros. La medida del número de valores que coinciden (elementos correctamente atribuidos) es una forma de determinar el error existente. El uso de la matriz de confusión es la forma más habitual de medir el error en la componente temática cuando esta es de tipo cualitativo. Veremos con más detalle su empleo y el de otras técnicas más complejas de similar propósito en el apartado Validacion .

Propagación de errores y modelación del error

El análisis de un dato espacial con errores va a dar un resultado que contiene a su vez errores, y existirá una relación directa entre los errores en el dato de partida y aquellos que aparecen en el dato resultante de su análisis. Este hecho se conoce como propagación de errores .

La propagación de errores puede ser muy variable en función del tipo de error que aparezca y la clase de análisis que se lleve a cabo. Errores de gran magnitud en el dato original pueden no tener apenas efecto en el resultado, mientras que pequeños errores pueden causar grandes alteraciones en la calidad de este [ Hengl2008Elsevier ].

Una de las áreas en las que más se ha trabajado en el estudio de la propagación de errores es el trabajo con Modelos Digitales de Elevaciones. Como veremos en el capítulo Geomorfometria , los MDE son un dato de primer orden, ya que resultan de utilidad en prácticamente cualquier tipo de proyecto SIG, y son muy numerosos los distintos parámetros que podemos derivar de ellos. Por esta razón, la propagación de errores es un asunto importante dentro del trabajo con un MDE, pues de él se van a obtener muchos datos nuevos, e interesa saber cómo la calidad de estos nuevos datos se va a ver afectada por la calidad del MDE de partida.

El error principal que se estudia en este tipo de análisis es el de los atributos, es decir, el de la elevación. Los datos empleados se basan en el modelo de representación ráster, ya que este es el más habitualmente empleado para los análisis de un MDE. No obstante, metodologías como la que veremos a continuación pueden aplicarse igualmente para la modelación de otros errores, tales como los errores posicionales en la digitalización de una capa vectorial.

La metodología más extendida para la modelación de errores es la basada en simulaciones de Monte Carlo. El fundamento de este método es considerar un dato espacial dado (un MDE para el caso de este ejemplo) como una de las posibles «versiones» de la realidad que pueden existir con una magnitud de error concreta. Evaluando el error existente en un dato espacial y su distribución, y realizando simulaciones estocásticas en base a este, pueden obtenerse otras de esas «versiones» de la realidad. Posteriormente, puede realizarse el análisis no sobre el MDE como tal, sino sobre todo ese conjunto de datos derivados del MDE y su distribución de error.

De este modo, se simula la presencia de error añadiendo ruido al MDE original, pero de una forma acorde con el propio error existente en el dato base. De las alternativas que se obtienen mediante estas simulaciones, ninguna de ellas tiene que ser necesariamente correcta y carente de errores [ Chrisman1989Autocarto ] (lo más probable es que ninguna lo sea), pero el conjunto define un intervalo probable en el cual se situarán los valores reales. Se modela así la incertidumbre existente en el dato y la forma en que esta se propaga a los datos derivados.

Para una operación dada a aplicar sobre un MDE, la forma de proceder puede resumirse en los siguientes pasos [ Heuvelink1998Taylor ]:

• Estudiar la distribución del error en el MDE en base a un juego de datos de referencia (generalmente un conjunto de puntos con mediciones precisas). Para modelizar el error no basta simplemente medir este con un parámetro como el error medio cuadrático, sino analizar su distribución y calcular parámetros estadísticos en base al conjunto de todos los errores medidos. Si se asume una distribución normal de los errores, la media y la desviación típica son necesarias para definir esa distribución.

  Al igual que sucede con los datos en sí, los errores tiene una dependencia espacial. Esto es, cerca de un valor que presenta un gran error, aparecerán otros también con errores notables, y cerca de valores donde el error es pequeño, no existirán puntos muy erróneos. La autocorrelación espacial, que veremos con detalle más adelante en este libro, se presenta tanto en los datos como en los errores.

  Por esta razón, la modelación del error requerirá conocer otros elementos adicionales para definir correctamente su distribución, tales como semivariogramas o correlogramas (estudiaremos estos en detalle en el capítulo Estadistica_espacial , dedicado a la estadística espacial).

• Utilizando la distribución de los errores, se generan un número $n$ de nuevos MDE. Para cada uno de ellos, se genera una capa aleatoria de errores que se ajusta a la distribución definida, y esta se suma al MDE original. De este modo, en lugar de una posible versión de la realidad, se tienen $n$ versiones.

  La existencia de dependencia espacial puede añadirse en este paso si no se considera en el anterior, mediante el procesado de las capas de error y la aplicación de filtros sobre estas.

• Se aplica la operación sobre cada una de las $n$ capas obtenidas.
• Se calculan parámetros estadísticos de los $n$ resultados obtenidos, a partir de los cuales puede crearse un resultado único. Por ejemplo, la media de los $n$ resultados obtenidos puede considerarse como valor resultante de la operación, en sustitución del que se obtendría aplicando esta únicamente al MDE original.

En la figura \ref{Fig:Esquema_MonteCarlo} se muestra un esquema gráfico de esta metodología.

$$\label{Fig:Esquema_MonteCarlo}$$

Para ver con más claridad el efecto de este proceso, la figura \ref{Fig:Simulaciones_MonteCarlo} muestra respectivamente los resultados obtenidos a partir de un MDE, y la media de 20 y 50 simulaciones obtenidas según lo explicado anteriormente para el calculo de la curvatura horizontal (esté parámetro se explica en el capítulo Geomorfometria ).

$$\label{Fig:Simulaciones_MonteCarlo}$$

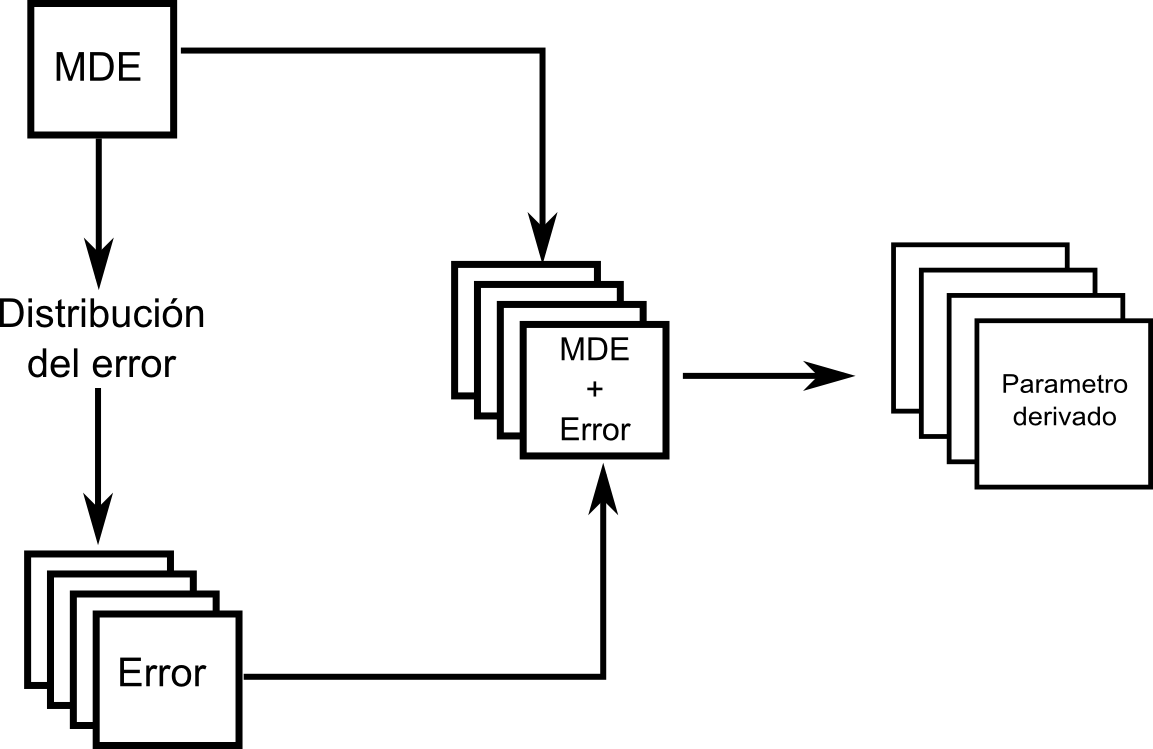
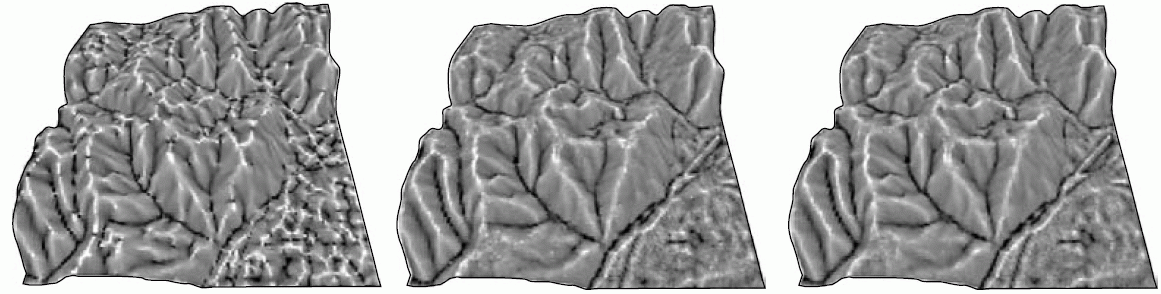
Pese a su importancia, las herramientas para estos análisis no se implementan de forma habitual en los SIG, sino que deben llevarse a cabo utilizando funcionalidades individuales de análisis y programando los procesos repetitivos que son necesarios para calcular todas las capas derivadas empleadas. Por esta razón, es extraño que estos procesos se lleven a cabo en proyectos SIG de modo genérico. El usuario de SIG es consciente de los errores que presentan los datos espaciales con los que trabaja y las implicaciones de estos en lo que respecta a la calidad de datos, pero raramente desarrolla procesos de modelación de la incertidumbre, que quedan por el momento reservados para un ámbito más teórico que práctico.

Gestión de errores

Conocidos los tipos de errores fundamentales que encontramos en los datos espaciales y la manera de medir estos y su propagación, deben formularse estrategias para tratar de reducir el error, así como definir metodologías que permitan obtener resultados más precisos dentro de un proyecto SIG.

Estas estrategias dependen, como es lógico, del tipo de proyecto, sus objetivos, o el tipo de dato que se emplee para su desarrollo.

Podemos dividir estas estrategias en dos grupos fundamentales:

• Utilización de datos de partida más precisos. Deben establecerse parámetros de calidad referidos a los datos con los que se trabaja, que permitan tener garantía de que estos están en condiciones de dar respuestas correctas a las cuestiones que planteemos en base a ellos.
• Minimización de los errores a lo largo del desarrollo del trabajo. No todas las operaciones que realizamos en un SIG implican la introducción de errores en la misma medida. La propagación del error puede controlarse si estructuramos adecuadamente los pasos a realizar, situando al final de la cadena de procesos aquellos que sean más propensos a generar errores o sobre los que se tenga más incertidumbre en cuanto a la calidad de los resultados que arrojan.

Con independencia de la forma en que la gestión de errores se aborde, es importante que a la hora de trabajar con un SIG se tengan en cuenta ciertas ideas fundamentales con objeto de evitar la introducción de errores innecesarios. Algunas de estas ideas se enumeran seguidamente:

• La utilización de capas de distintos orígenes y en distintos formatos favorece la aparición de errores y puede dar lugar a resultados de precisión insuficiente [ Vitek1984Pecora ].
• La precisión disminuye a medida que lo hace la resolución espacial [ Walsh1987PERS ].
• La precisión de un resultado nunca sera superior a la del dato de entrada con peor precisión [ Newcomer1984TAC ].
• Cuanto mayor es el número de capas empleadas para un análisis, mayores oportunidades existen de incorporar error a este e imprecisión a los resultados [ Newcomer1984TAC ].

Es igualmente importante recalcar el hecho de que los datos digitales con los que trabajamos en un SIG no son per se mejores que los datos analógicos en cuanto a su precisión y su falta de errores. Si bien existen muchas ventajas asociadas a los datos digitales, tal y como vimos en el capítulo Fuentes_datos , la precisión no ha de ser necesariamente una de ellas, o al menos no como para poder asumir que su naturaleza digital implica que un dato es de calidad suficiente. En ocasiones, los usuarios de SIG pueden olvidar esto y trabajar bajo unas suposiciones incorrectas, introduciendo errores en sus resultados y no siendo conscientes de ello.

La importancia de los metadatos es grande en este sentido, ya que la cartografía impresa habitualmente contiene información acerca de su calidad y su precisión, pero al trabajar con una capa en un SIG, esa información la contienen los metadatos. Mientras que en un mapa impreso no podemos separar el mapa en sí de esa información, en el contexto de capas de un SIG estas se encuentran formalmente separadas, hasta tal punto que la práctica más habitual es trabajar con capas sin metadatos o, de existir estos, no emplearse como parte importante de los propios datos.

Resumen

Pese a no haber sido una preocupación importante en los comienzos de los SIG, la calidad de los datos geográficos es hoy en día un aspecto clave para el trabajo con SIG. Las etapas fundamentales relativas a la calidad de los datos son la identificación de la fuente de error, su detección y medición, su modelación y, por último, la gestión de dicho error.

Las fuentes de error principales son las deficiencias de los datos originales, los errores conceptuales, los derivados de los procesos de digitalización y los introducidos en la realización de procesos con los datos. Estas fuentes introducen errores de posicionamiento, errores en los atributos asociados o de coherencia topológica, entre otros. Estas son algunas de las denominadas componentes de la calidad , entre las que también encontramos la procedencia de los datos o su validez temporalc.

Los errores aparecen de forma distinta en función de las características de los datos, en particular del modelo de representación elegido.

Detectar los errores puede realizarse de forma visual o bien de forma analítica, pudiendo automatizarse en este segundo caso. El error medio cuadrático es la medida más habitual del error en el caso de variables cuantitativas, mientras que la matriz de confusión es empleada para variables cualitativas.

Modelar el error y su propagación puede emplearse para conocer de forma más adecuada la validez de los resultados obtenidos a partir de un dato espacial. La realización de simulaciones condicionales mediante el método de Monte Carlo es la técnica más habitual para la modelación de errores.

Por último, es importante ser consciente de los errores que contienen los datos y de la posible aparición de estos a medida que realizamos tareas con ellos, con objeto de minimizar dicha aparición y limitar la presencia e influencia de los errores en los resultados finales.