Estadísticas espaciales

Introducción

La información espacial es susceptible de ser analizada estadísticamente como cualquier otro tipo de información. Una serie de $n$ datos recogidos en otros tantos puntos no deja de ser una serie de datos sobre la que pueden aplicarse las técnicas estadísticas habituales. Junto a ello, cada uno de estos datos tiene asociada una coordenada, y esta aporta una información adicional que puede emplearse igualmente para obtener resultados estadísticos de diversa índole.

Si trabajamos en el plano cartesiano, en lugar de una serie de valores de una variable $a$ disponemos de una serie de ternas $(x,y,a)$. Extendiendo la posibilidad de analizar estadísticamente los valores $a$ recogidos en esa serie de localizaciones, encontramos otras dos formas de analizar este conjunto.

Analizar la disposición espacial, con independencia de los valores. Es decir, estudiar el conjunto de pares de valores $(x,y)$
Analizar la disposición espacial y los valores recogidos. Es decir, estudiar el conjunto de ternas $(x,y,a)$

Este tipo de análisis se lleva a cabo preferentemente sobre capas de tipo punto, aunque algunas de estas formulaciones pueden igualmente aplicarse a capas ráster, considerando que cada celda conforma de igual modo una terna de valores.

Dentro de este capítulo analizaremos algunos de los analisis estadísticos espaciales más básicos, como son los siguientes:

Medidas centrográficas . El equivalente espacial de las medidas de tendencia central como el momento de primer orden (media) o la mediana, así como de las de dispersión tales como el momento de segundo orden (desviación típica).
Análisis estadístico de líneas . Descriptores estadísticos para líneas y ángulos.
Análisis de patrones de puntos . Este tipo de análisis permite caracterizar la estructura espacial de un conjunto de puntos en función de parámetros como la densidad o las distancias entre puntos y su configuración en el espacio.
Autocorrelación espacial . Los puntos cercanos tienden a tener valores más similares entre sí que los puntos alejados. Este fenómeno puede cuantificarse y estudiarse con una serie de índices, así como mediante elementos tales como variogramas o correlogramas.

Otro grupo de procedimientos con componente estadística, los relativos a las técnicas de interpolación, se verán en un capítulo independiente (Capítulo Creacion_capas_raster ). De igual modo, aquellos que permiten el calculo de densidades se recogen también en dicho capítulo.

Un capítulo dedicado a la aplicación de otras técnicas estadísticas más complejas tales como técnicas de agrupación o regresiones espaciales (Capitulo Estadistica_avanzada ) completa este grupo de secciones dedicadas a los elementos estadísticos.

Medidas centrográficas

Las medidas centrográficas representan descriptores básicos de los datos espaciales, extendiendo las medidas de tendencia central y dispersión de la estadística clásica al ámbito espacial.

La principal medida de tendencia central espacial es el centro medio . El centro medio es un punto cuyas coordenadas son la media en cada eje de las coordenadas de los puntos analizados (Figura \ref{Fig:Centro_medio_y_desviacion}).

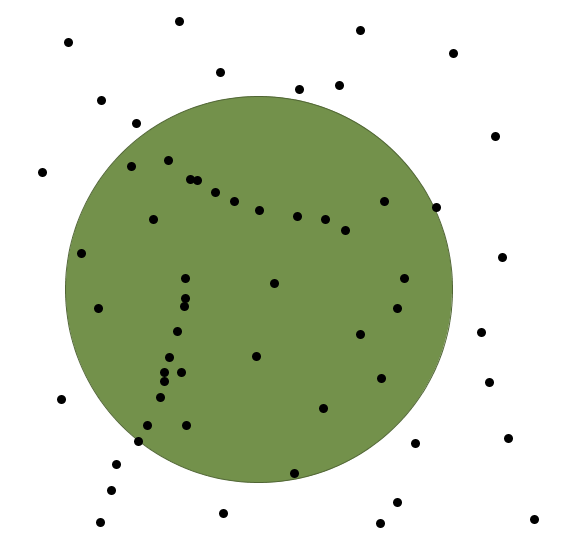
Circulo de radio igual a la distancia típica centrado en el centro medio del conjunto.

$$\label{Fig:Centro_medio_y_desviacion}$$

Es decir, el punto $(\overline{x}, \overline{y})$ tal que

\begin{eqnarray} \overline{x} = \frac{\sum_{i=1}^n x_i}{N} \\ \overline{y}= \frac{\sum_{i=1}^n y_i}{N} \nonumber \end{eqnarray}

Cada uno de los puntos puede ponderarse según el valor recogido en él, de forma que lo anterior quedaría como

\begin{eqnarray} \overline{x} = \frac{\sum_{i=1}^N a_i x_i}{\sum_{i=1}^N a_i} \\ \overline{y} = \frac{\sum_{i=1}^N a_i y_i}{\sum_{i=1}^N a_i} \nonumber \end{eqnarray}

El centro medio es el centro de gravedad del conjunto de puntos, tomando como masa de cada uno el valor asociado a este. Asimismo, es el punto que minimiza la suma de distancias al cuadrado, esto es, la expresión

\begin{equation} \sum_{i=1}^N d_{ic} = \sum_{i=1}^N (\overline{x} - x_i)^2 + (\overline{y} - y_i)^2 \end{equation}

Un uso habitual del centro medio lo encontramos en los estudios demográficos, que pueden analizar la evolución de las poblaciones sobre el territorio estudiando cómo se ha desplazado su centro medio a través del tiempo.

El equivalente espacial de la mediana es el centro mediano . Al igual que el centro medio, el centro mediano es también un punto. En este caso sus coordenadas son las medianas de las de los puntos analizados en cada eje [ Cole1968Wiley ].

Puede ser interesante también analizar el centro mediano como una línea en lugar de un punto. Por ejemplo, una línea vertical que pasa por la componente en $x$ del centro mediano. Si trabajamos con una serie de puntos que representan poblaciones y estos se ponderan según su número de habitantes, esta línea divide el territorio en dos zonas igualmente pobladas. La mitad de los habitantes viven a un lado de ella, y la otra mitad al otro lado.

En la figura \ref{Fig:Centro_mediano} puede verse una representación de lo anterior.

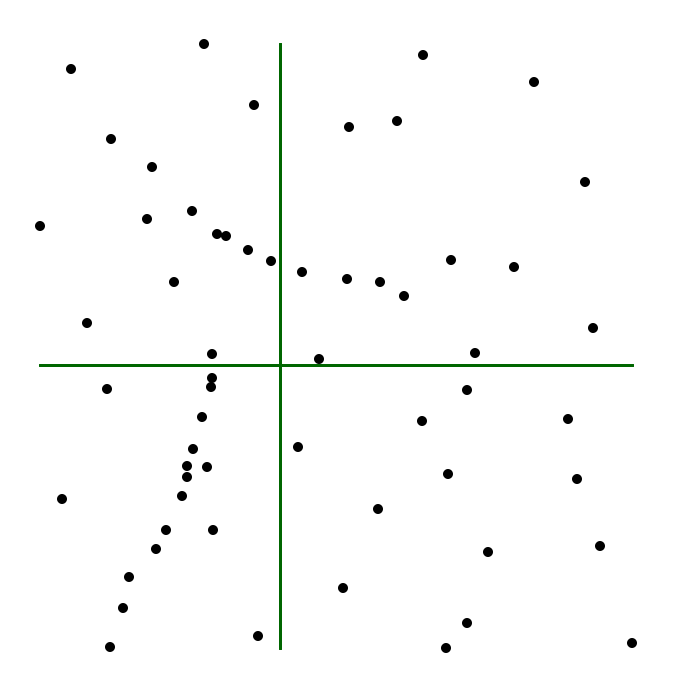
Centro mediano y líneas de división pasando por este, las cuales dividen el conjunto de puntos en dos partes iguales a Este y Oeste, y Norte y Sur, respectivamente.

El inconveniente del centro mediano es que depende de los ejes escogidos y no es por tanto invariante ante rotaciones. Para solucionar esto suele emplearse como definición alternativa la de aquel punto del espacio que hace mínima la suma de distancias a todos los puntos de datos[ King1962Prentice ]. El cálculo de este punto requiere de un proceso iterativo [ Rogerson2001Sage ] en el cual se tiene que

\begin{eqnarray} x = \frac{\sum_{i=1}^N \frac{d_i}{a_i}x_i}{\sum_{i=1}^N \frac{d_i}{a_i}} \\ y = \frac{\sum_{i=1}^N \frac{d_i}{a_i}y_i}{\sum_{i=1}^N \frac{d_i}{a_i}} \nonumber \\ \end{eqnarray}

donde $d_i$ es la distancia del punto i-ésimo a la localización del centro mediano en la iteración actual. Como primera coordenada para iterar, una buena elección es el propio centro medio. El proceso se detiene cuando la distancia entre el nuevo centro mediano y el de la iteración anterior es menor que un determinado umbral establecido de antemano.

Respecto a las medidas de dispersión, el equivalente a la desviación típica es la denominada distancia típica , cuya expresión es la siguiente [ Bachi1963RSA ]

\begin{equation} s_d = \sqrt{\frac{\sum_{i=1}^n d^2_i}{n}} \end{equation}

siendo $d_i$ la distancia entre el punto i-ésimo y el centro medio.

También puede escribirse lo anterior como

\begin{equation} s_d = \sqrt{\left(\frac{\sum_{i=1}^N x_i^2}{N} - \overline{x}^2 \right) + \left(\frac{\sum_{i=1}^N y_i^2}{N} - \overline{y}^2 \right)} \end{equation}

Es interesante comentar que la distancia a la media en el concepto habitual de desviación típica puede ser positiva o negativa (de ahí que se eleve al cuadrado y después se aplique la raíz), mientras que en el caso espacial es siempre positiva.

Una forma de representar esta distancia típica es mediante un circulo de radio dicha distancia centrado en el centro medio (Figura \ref{Fig:Centro_medio_y_desviacion})

La distancia típica puede, igualmente, calcularse ponderando los distintos puntos, quedando su expresión como

\begin{equation} s_d = \sqrt{\frac{\sum_{i=1}^n a_i d_i^2}{\sum_{i=1}^N a_i}} \end{equation}

Mediante esta representación se asume, no obstante, que la dispersión es la misma en todas direcciones. Esta simplificación raramente es cierta, y es más correcto definir en lugar de un círculo una elipse de desviación . Esta elipse de desviación viene definida por sus semiejes mayor y menor, en los cuales se dan, respectivamente, la mayor y menor dispersión.

El ángulo $\alpha$ que define al semieje mayor $x'$ viene expresado según

\begin{eqnarray} \tan{\alpha} = \frac{\sum_{i=1}^N dx_i - \sum_{i=1}^N dy_i}{2\sum_{i=1}^N dx_i dy_i} \nonumber \\ + \frac{\sqrt{\left(\sum_{i=1}^N dx_i - \sum_{i=1}^N dy_i \right)^2 +4\sum_{i=1}^N dx_i dy_i}}{2\sum_{i=1}^N dx_i dy_i} \nonumber \end{eqnarray}

siendo $dx_i$ y $dy_i$ las distancias en los ejes $x$ e $y$ respectivamente entre el punto i--ésimo y el centro medio.

El semieje menor es perpendicular al anterior.

Las distancias típicas en cada uno de estos dos semiejes vienen expresadas por

\begin{eqnarray} \delta_{x'} &=& \bigg(\sum_{i=1}^N dx^2_i \cos^2{\alpha} \nonumber\\ &&{} + 2\left(\sum_{i=1}^N dx_i dy_i\right)\sin{\alpha}\cos{\alpha} \nonumber \\ &&{} + \sum_{i=1}^N dy_i^2 \sin^2{\alpha}\bigg)^{\frac{1}{2}} \end{eqnarray}

\begin{eqnarray} \delta_{y'} &=& \bigg(\sum_{i=1}^N dx^2_i \sin^2{\alpha} \nonumber\\ &&{} + 2\left(\sum_{i=1}^N dx_i dy_i\right)\sin{\alpha}\cos{\alpha} \nonumber \\ &&{} + \sum_{i=1}^N dy_i^2 \cos^2{\alpha}\bigg)^{\frac{1}{2}} \end{eqnarray}

Por último, la medida de desviación relativa que equivale en la estadística espacial al coeficiente de variación es la distancia relativa [ McGrew1993William ], que se calcula dividiendo la distancia típica por el radio de un círculo con el mismo área que la zona de estudio. Si esta zona es circular, se tiene por tanto

\begin{equation} s_{d,rel} = \frac{s_d}{R} \end{equation}

siendo $R$ el radio de la zona de estudio.

En caso de que esta zona sea cuadrada y de área $A$ , se tiene que

\begin{equation} s_{d,rel} = \frac{s_d\sqrt{\pi}}{\sqrt{A}} \end{equation}

En la figura \ref{Fig:Distancia_relativa} puede verse cómo distribuciones espaciales iguales (con la misma distancia típica) representan dispersiones relativas distintas en relación a la zona de estudio.

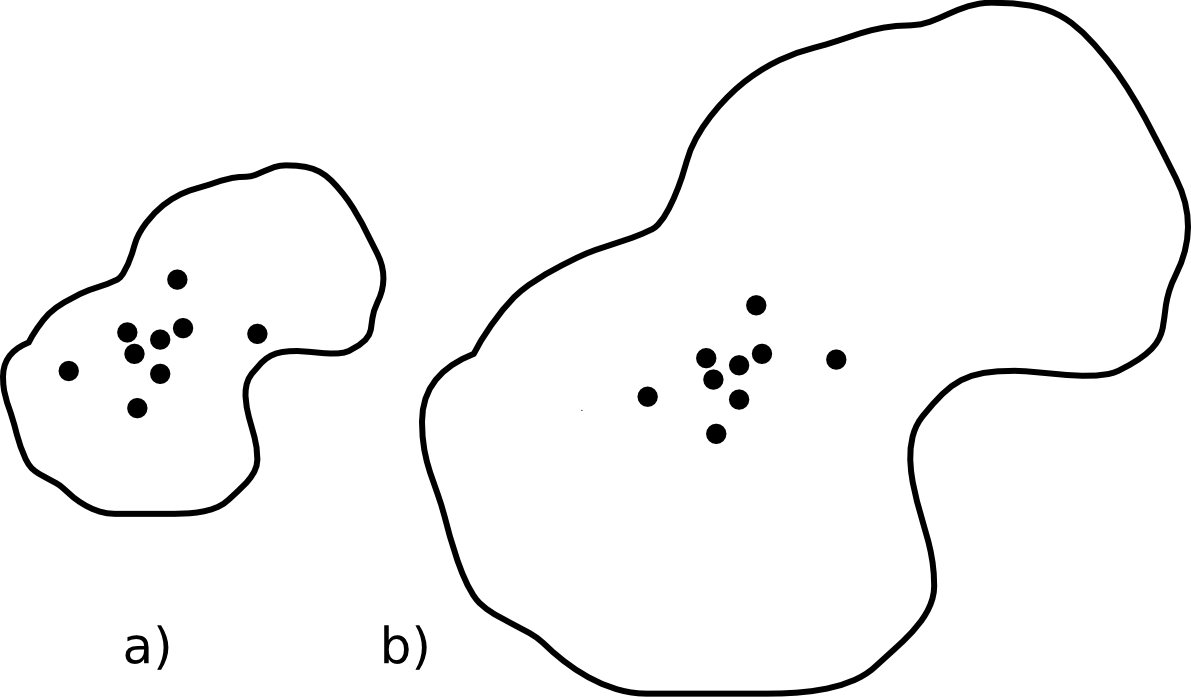
Aunque ambas distribuciones tienen la misma distancia típica, la dispersión en relación al área analizada es distinta, con lo que los valores de distancia relativa serán distintos.

Estadísticas sobre líneas. Variables circulares

Dentro de los objetos geográficos, las líneas merecen algunos comentarios aparte en lo que a su análisis respecta. Tanto las líneas como los polígonos pueden ser reducidos en ultima instancia a puntos (los polígonos bien por sus puntos constituyentes o bien por el centroide, el cual coincide con el centro medio), y analizados estos con algunas de las fórmulas antes vistas o las que se verán más adelante. La particularidad de las líneas estriba en que, además de valores puntuales o de área (como los de los polígonos), definen igualmente direcciones y ángulos de giro entre sus segmentos. El análisis estadístico de variables circulares como estas presenta sus propias particularidades, que deben conocerse para poder extraer resultados correctos a partir de datos de esta índole.

Un ejemplo del uso de variables direccionales lo encontramos, por ejemplo, en el estudio de desplazamientos de animales cuyas rutas hayan sido monitorizadas y se encuentren dentro de un SIG como capas de líneas. Un situación similar se da en el caso de elementos que no representen un movimiento pero tengan dirección, tales como fallas u otros elementos geológicos. Más alla de casos como estos, los conceptos relativos a este tipo de variables también tienen aplicación para cualquier información similar, con independencia de su formato de almacenamiento. Así, son de aplicación, entre otros, para el estudio de orientaciones dentro del análisis geomorfométrico (Capítulo Geomorfometria ), el cual se lleva a cabo fundamentalmente sobre capas ráster.

En el caso que nos ocupa del estudio de líneas, pueden considerarse todos y cada uno de los segmentos de estas como líneas en sí, o bien la línea ficticia que une el inicio del primer segmento con el final del último.

A continuación se mostrarán brevemente los estadísticos más frecuentes para datos circulares, con especial énfasis en su aplicación al análisis de líneas dentro de un SIG. Descripciones más detalladas de estos y otros elementos de estadística circular, junto a sus aplicaciones en áreas donde el empleo de SIG es habitual, pueden consultarse en [ Batchelet1981Academic ] o [ Fisher1993Cambridge ].

Para comenzar, el cálculo de la media de dos ángulos ejemplifica bien las particularidades de los datos circulares. Sean tres ángulos de 5°, 10° y 15° respectivamente. El concepto habitual de media aplicado a estos valores resultaría en un ángulo medio de 10°, correcto en este caso. Si giramos ese conjunto de ángulos 10 grados en sentido antihorario, dejándolos como 355°, 0°, 5°, la media debería ser 0°, pero en su lugar se tiene un valor medio de 120°.

Una forma correcta de operar con ángulos $\alpha_1,…,\alpha_n$ consiste en hacerlo con las proyecciones del vector unitario según dichos ángulos, es decir $\sin{\alpha_1},….\sin{\alpha_n}$ y $\cos{\alpha_1},….\cos{\alpha_n}$. Aplicando luego los estadísticos habituales sobre estos valores se obtienen unos nuevos valores de senos y cosenos que permiten obtener el ángulo resultante aplicando sobre ellos la función arcotangente.

En el caso de segmentos orientados tales como los que constituyen las líneas dentro de una capa de un SIG, resulta conveniente tratar cada segmento como un vector. La resultante de su suma vectorial será otro vector con la dirección media de todos los segmentos, y cuyo módulo (longitud) aporta información acerca de la tendencia y variación de las direcciones a lo largo de la linea. Si la dirección es uniforme, el módulo será mayor, siendo menor si no lo es (Figura \ref{Fig:Media_vectorial}). El vector resultante puede dividirse por el número total de segmentos iniciales para obtener una media vectorial.

Media vectorial (en rojo) de una serie de segmentos.

Es decir, se tiene un vector cuya orientación viene definida por un ángulo $\overline\alpha$ tal que

\begin{equation} \overline\alpha = \arctan{\frac{S}C} \end{equation}

y con un módulo $\overline{R}$ según

\begin{equation} \overline{R} = \frac{\sqrt{S^2 + C^2}}N \end{equation}

siendo $S$ y $C$ las sumas de senos y cosenos, respectivamente. \begin{equation} S = \sum_{i=1}^N \sin{\alpha_i} \qquad ; \qquad S = \sum_{i=1}^N \cos{\alpha_i} \end{equation}

El módulo $\overline{R}$ se conoce también como concentración angular y es una medida inversa de la dispersión angular. No obstante, hay que tener en cuenta que valores próximos a cero, los cuales indicarían gran dispersión, puede proceder de dos agrupaciones de ángulos similares (es decir, con poca dispersión) si estas agrupaciones se diferencian entre sí 180°.

Cuando se trabaja con direcciones en lugar de orientaciones, es frecuente multiplicar por dos los valores angulares y posteriormente simplificar el ángulo aplicando módulo 360°. Es decir, aplicar la transformación $\alpha' = 2\alpha \mod 360°$.

La forma en que las distintas orientaciones se congregan en torno a la media, relacionada directamente con la dispersión, puede servir para inferir la existencia de una dirección predominante o bien que los valores angulares se hallan uniformemente distribuidos. La comprobación de que existe una tendencia direccional es de interés para el estudio de muchos procesos tales como el estudio de movimiento de individuos de una especie, que puede denotar la existencia de una línea migratoria preferida o revelar la presencia de algún factor que causa dicha predominancia en las direcciones.

Existen diversos test que permiten aceptar o rechazar la hipótesis de existencia de uniformidad, entre los cuales destacan el test de Rayleigh, el test V de Kuiper [ Kuiper1960Akad ] o el test de espaciamiento de Rao [ Rao1969PhD ]

Para este último, se tiene un estadístico $U$ según

\begin{equation} U = \frac{1}2\sum_{i=1}^N \|T_i - \lambda\| \end{equation}

siendo

\begin{equation} \lambda = \frac{360}N \end{equation}

\begin{equation} T_i = \left\{ \begin{array}{ll} \alpha_{i+1} - \alpha_i & \textrm{si $1 \leq i \lt N-1$}\\ 360 - \alpha_n + \alpha_1 & \textrm{si $i = N$} \end{array} \right. \end{equation}

Puesto que las desviaciones positivas deben ser iguales a las negativas, lo anterior puede simplificarse como

\begin{equation} U = \sum_{i=1}^N (T_i - \lambda) \end{equation}

Para un numero de puntos dado y un intervalo de confianza establecido, los valores de $U$ están tabulados, y pueden así rechazarse o aceptarse la hipótesis nula de uniformidad. Dichas tablas pueden encontrarse, por ejemplo, en [ Russell1995CSSC ].

Análisis de patrones de puntos

Las coordenadas de un conjunto de puntos no solo representan una información individual de cada uno de ellos, sino de igual modo para todo el conjunto a través de las relaciones entre ellas. La disposición de una serie de puntos en el espacio conforma lo que se conoce como un patrón de puntos , el cual puede aportar información muy valiosa acerca de las variables y procesos recogidos en dichos puntos. Por ejemplo, si estos representan lugares donde se han observado individuos de una especie, su distribución espacial puede servir como indicador de la interacción entre dichos individuos o con el medio.

La caracterización de un patrón de puntos es, por tanto, de interés para la descripción de estos, y se realiza a través de análisis estadísticos y descriptores que definen la estructura del mismo.

Para llevar a cabo este análisis se asume que la estructura espacial de un patrón dado es el resultado de un proceso puntual . Se entiende por proceso puntual un proceso estocástico que genera tales patrones, compartiendo todos ellos una similar estructura (la ley de dicho proceso). Los puntos son eventos de dicho proceso. Describiendo el tipo de patrón se obtiene información sobre el proceso puntual que lo ha originado.

Podemos encontrar múltiples ejemplos de procesos puntuales, tales como la disposición de individuos de una especie, la disposición de los árboles en un bosque o la aparición de casos de una enfermedad. Cada uno de ellos tiene sus propias características.

Como se puede observar en la figura \ref{Fig:Patrones_puntos}, existen tres tipos de patrones que un proceso de puntos puede generar:

Agregado . La densidad de los puntos es muy elevada en ciertas zonas.
Aleatorio . Sin ninguna estructura, las posiciones de los puntos son independientes entre sí.
Regular . La densidad es constante y los puntos se disponen alejados entre sí.

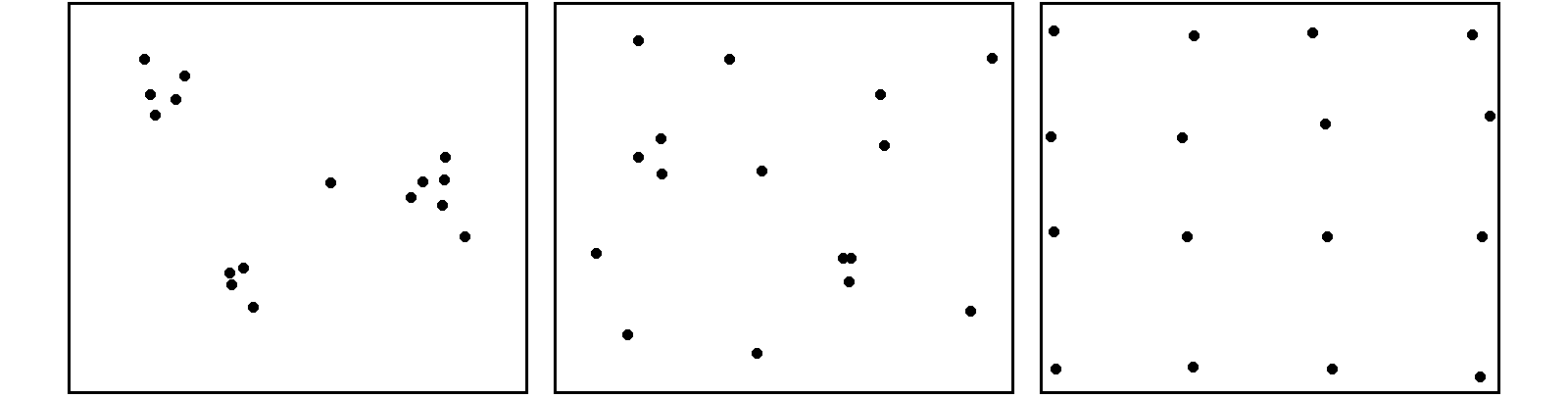
De izquierda a derecha, patrones de puntos agregado, aleatorio y regular.

El análisis de patrones de puntos se fundamenta básicamente en la comparación entre las propiedades de una distribución teórica aleatoria (distribución de Poisson) y las de la distribución observada. La distribución teórica aleatoria cumple que se da aleatoriedad espacial completa (CSR, Complete Spatial Randomness , en inglés). De este modo, se puede decidir si la distribución observada es también aleatoria en caso de existir similitud, o bien es de alguno de los dos tipos restantes, según sea la discrepancia existente.

Las propiedades a comparar pueden ser:

Propiedades de primer orden . La intensidad del proceso $\lambda(h)$, definida como la densidad (número de puntos por unidad de área). En general, se asume que es una propiedad estacionaria, esto es, constante a lo largo de la zona de estudio. Existen distribuciones como la distribución no homogénea de Poisson que asumen una variabilidad de la intensidad a lo largo de la zona de estudio. En el apartado Densidad veremos cómo crear capas continuas de esta intensidad $\lambda(h)$.
Distancia entre puntos . Relaciones entre cada punto con los de su entorno. Basado en las denominadas propiedades de segundo orden .

Análisis de cuadrantes

En el primero de los casos, la metodología de análisis de cuadrantes divide la zona de estudio en unidades regulares, cuadrantes , y estudia el número de puntos que aparecen dentro de cada una.

La forma de estas unidades puede ser cualquiera, aunque lo habitual es emplear unidades cuadradas, de ahí la denominación. Debido a los efectos de escala, el tamaño de estas unidades tiene una gran influencia en los resultados obtenidos. Un tamaño habitual es el doble del área media disponible para cada punto, es decir, cuadrados cuyo lado tendrá una longitud

\begin{equation} l = \sqrt{\frac{2A}{N}} \end{equation}

siendo $N$ el número de puntos y $A$ el área de la zona de estudio.

Con la serie de datos que indica el conteo de puntos en cada cuadrante, se procede al análisis estadístico. Este puede hacerse comparando los conteos en los cuadrantes o según la relación entre la media y la varianza de la serie. En este segundo caso, partimos de que en una distribución aleatoria es de esperar una varianza igual a la media [ Cressie1991Wiley ]. Por tanto, el cociente entre la varianza y la media debe ser cercano a 1. Si en la distribución analizada este cociente está próximo a ese valor, se tratará de una distribución aleatoria. En una distribución uniforme, la varianza (y por tanto el cociente con la media) será cercana a 0. En las distribución agrupadas, la varianza sera mayor, y el cociente por tanto superior a 1.

El análisis de cuadrantes no es en realidad una medida del patrón, sino de la dispersión. Además, debido al uso de una unidad de análisis (el cuadrante) fija, puede no ser capaz de localizar agrupamientos locales en esta.

Otra debilidad de este método es que no es capaz de diferenciar entre distribuciones tales como las de la figura \ref{Fig:Debilidad_cuadrantes}, claramente distintas pero que arrojan un resultado idéntico al aplicar esta metodología con los cuadrantes mostrados.

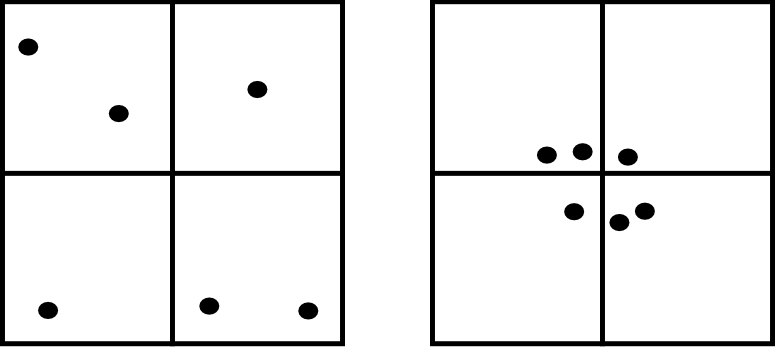
Dos disposiciones de puntos distintas que darían un mismo resultado al analizarse por el método de cuadrantes.

No obstante, la aplicación de este método en campos como la biología es muy habitual, y se han desarrollado numerosas extensiones del mismo tales como el índice de David--Moore [ David1954AnnalsBotany ], el índice de frecuencia de agregados [ Douglas1975Sankhya ], o el índice $I_{\delta}$ de [ Morisita1959Kyushu ], entre otros muchos.

Análisis de vecino más cercano

El método de vecino más cercano [ Evans1954Ecology ] permite solventar algunos de los problemas asociados al análisis de cuadrantes. Para ello, se basa en las distancias de cada punto a su vecino más cercano. Comparando estas distancias con el valor que cabe esperar en una distribución aleatoria, puede deducirse el tipo de estructura en la distribución observada.

El valor que define el patrón de puntos a estudiar es el índice de vecino más cercano , que se calcula como

\begin{equation} I_{mc} = \frac{\overline{d}_{mc}}{E(\overline{d}_{mc})} \end{equation}

siendo $\overline{d}_{mc}$ la media de las distancias al punto más cercano, según

\begin{equation} \overline{d}_{mc} = \frac{\sum_{i=1}^N d_{mc}}{N} \end{equation} $E(\overline{d}_{mc})$ es la media esperada en una distribución de Poisson, y se calcula según la expresión

\begin{equation} \hat{\mu} = \frac{1}{2\sqrt{\lambda}} \end{equation} siendo $\lambda$ la densidad de puntos por unidad de área, es decir

\begin{equation} \lambda = \frac{N}{A} \end{equation}

[ Donelly1978Cambridge ] propone corregir lo anterior para tener en cuenta los efectos de borde, utilizando la siguiente expresión:

\begin{equation} \hat{\mu} = \frac{1}{2\sqrt{\lambda}} + 0.0514 + \frac{0.041}{\sqrt{N}} \frac{B}{N} \end{equation}

donde $B$ es la longitud del perímetro del área estudiada.

El índice de vecino más cercano tiene un valor de 1 en una distribución aleatoria, menor de 1 en una distribución agregada, y mayor en una regular.

La desviación típica de las distancias se estima según

\begin{equation} \hat{\sigma}_{d} = \sqrt{\frac{4-\pi}{4\pi \frac{N^2}{A}}} \end{equation}

Aplicando como en el caso de la media una corrección de los efectos de borde, se tiene

\begin{equation} \hat{\sigma}_{d} = \sqrt{0.070 \frac{A}{N^2} + 0.037B\sqrt{\frac{A}{N^5}}} \end{equation}

Conociendo este resultado y que bajo la hipótesis de aleatoriedad espacial completa puede asumirse una distribución normal de los valores de distancia con la media y la desviación típica anteriores, pueden hacerse test de significación para conocer con qué grado de confianza es posible afirmar que la distribución analizada es o no aleatoria.

El análisis de vecino más cercano puede ampliarse al de los $n$ vecinos más cercanos. No obstante, este tipo de formulaciones se implementan con mucha menor frecuencia y son significativamente más complejas que las basadas en un único punto vecino.

Función K de Ripley

El problema de escala vimos que era patente en el método del análisis de cuadrantes, puesto que existía una fuerte dependencia del tamaño del cuadrante. La función K de Ripley trata de incorporar la escala como una variable más del análisis, convirtiendo dicha dependencia en un hecho favorable en lugar de una desventaja.

Para ello, en lugar de fijar una escala de análisis y una serie fija de cuadrantes de análisis, se tiene una serie aleatoria de zonas de análisis, las cuales se estudian a distintas escalas (con distintos tamaños). Para un proceso puntual dado, se trata de obtener una función que indique cuál es el numero de ocurrencias que deben darse a una distancia menor que un umbral dado $h$ de cualquier punto generado por dicho proceso. La función que cumple esta definición se denomina función K [ Ripley1977JRSS ], y puede expresarse como

\begin{equation} K(h) = \frac{1}{\lambda} E(n) \end{equation}

donde $n$ es el número de eventos a distancia menor que $h$ de un evento aleatorio cualquiera. La intensidad $\lambda$ se añade para eliminar la influencia de la densidad, ya que el valor esperado de puntos a una distancia dada está en relación directa con dicha densidad.

Tiene sentido estudiar esta función tan solo para valores de $h$ pequeños en comparación con el tamaño de la zona de estudio, ya que para otros valores no resulta coherente analizar los efectos de segundo orden dentro de dicha zona. Por ello, lo habitual es aplicar esta función solo a los valores de $h$ menores que la mitad de la dimensión menor de la zona de estudio.

Un estimador de la función K es

\begin{equation} \label{Eq:Ripley} \hat{K}(h) = \frac{1}{\lambda^2 A}\sum_{i=1}^N\sum_{j=1, j\neq i}^N I_h(d_{ij}) \end{equation}

siendo $I_h$ una función indicadora de la forma

\begin{equation} I_h(d_{ij} = \left \{ \begin{array}{ll} 1 & \textrm{ si } d_{ij} \leq h \\ 0 & \textrm{ si } d_{ij} > h \\ \end{array}\right. \end{equation}

En este estimador no se consideran los efectos de borde, y aquellos puntos situados cerca de la frontera de la zona de estudio tendrán estimaciones inferiores a las reales. Un estimador que corrige estos efectos [ Ripley1977JRSS ] es el siguiente:

\begin{equation} \label{Eq:Ripley_estimador} \hat{K}(h) = \frac{1}{\lambda^2 A}\sum_{i=1}^N\sum_{j=1, j\neq i}^N \frac{I_h(d_{ij})}{w_{ij}} \end{equation}

El valor $w_ij$ pondera los distintos puntos en función de su distancia al borde de la zona de estudio. Para calcularlo se traza una circunferencia por el punto $i$ con radio $d_{ij}$ (es decir, una circunferencia con centro en el punto $i$ y que pasa por el punto $j$), siendo $w_{ij}$ la fracción de dicha circunferencia que queda dentro de la zona de estudio (Figura \ref{Fig:Correcion_Ripley}).

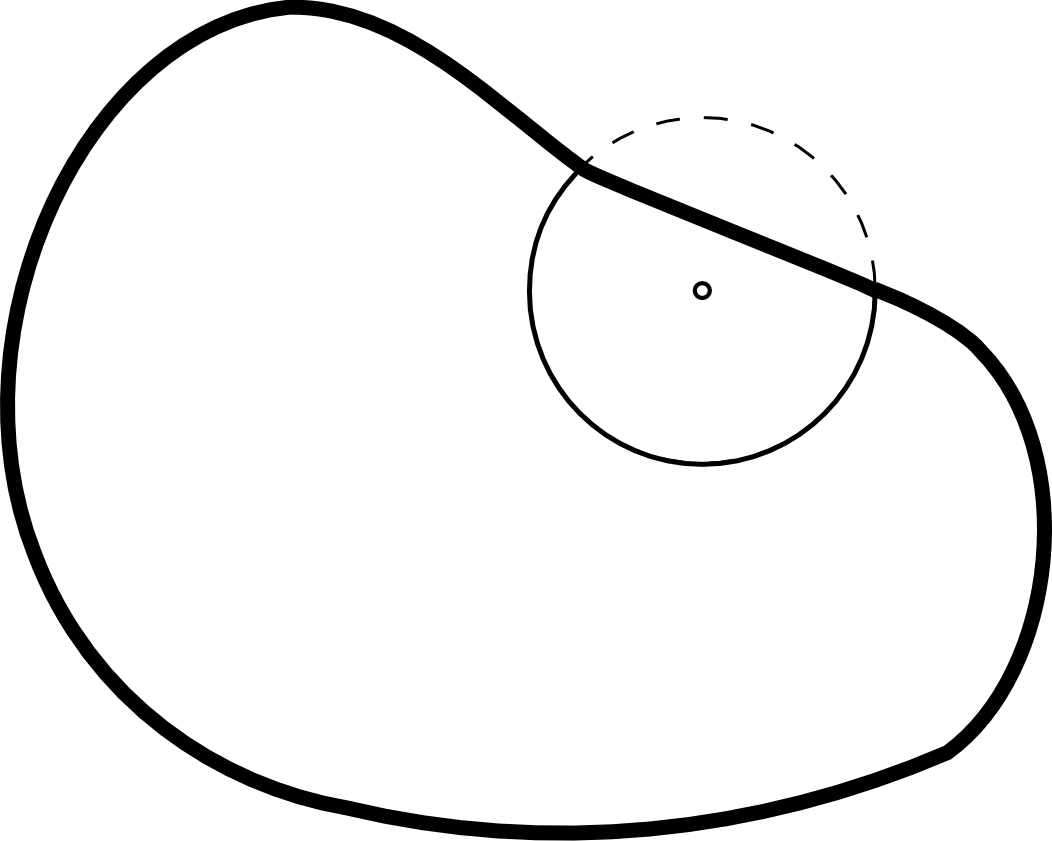
Corrección del estimador $\hat{K}(h)$ en función de los efectos de borde. El parámetro de corrección es el cociente entre la longitud interior (en trazo continuo) y la total de la circunferencia

Hay que tener en cuenta que en ocasiones no es conveniente aplicar el efecto de borde, por ejemplo en el caso en que el proceso puntual subyacente no tenga lugar fuera de la zona de estudio.

Puesto que la densidad se estima como $\lambda = \frac{N}{A}$, la expresión del estimador de la función K queda finalmente como

\begin{equation} \hat{K}(h) = \frac{A}{N^2}\sum_{i=1}^N\sum_{j=1, j\neq i}^N \frac{I_h(d_{ij})}{w_{ij}} \end{equation}

Para interpretar el significado de la función K, se tiene que, en condiciones de aleatoriedad espacial completa, el número de eventos a una distancia menor que $h$ es $\pi h^2$. Esto es, $K(h) = \pi h^2$. Comparando los valores esperados con los estimados, se tiene que si $\hat{K}(h) < K(h)$ existe agrupamiento, mientras que si $\hat{K}(h) > K(h)$ existe regularidad en la distribución.

Para esta interpretación resulta más habitual utilizar un estimador $ \hat{L}(h)$ de la forma

\begin{equation} \hat{L}(h) = \sqrt{\frac{\hat{K}(h)}{\pi}} - h \end{equation}

de tal modo que valores positivos de la misma indican agregación, mientras que los negativos indican regularidad.

Además de comparar el valor estimado con el valor esperado de la función K en condiciones de aleatoriedad espacial completa, puede compararse con el esperado para un proceso puntual determinado. Los valores de la función K son conocidos para muchos procesos puntuales, y esa información puede utilizarse para establecer comparaciones de igual modo. Distribuciones como las de Cox[ Cox1980Chapman ] o Gibbs han sido empleadas frecuentemente para el análisis de fenómenos tales como las distribuciones de pies dentro de masas forestales.

Frente a este enfoque, existe también la posibilidad de realizar un número $n$ (preferiblemente grande) de simulaciones de un proceso y calcular la media y desviación típica de los valores de la función K obtenidos en ellas. Con ellos puede posteriormente calcularse la probabilidad de que una distribución observada de puntos represente un resultado generado por dicho proceso.

Al igual que los métodos restantes, el empleo de funciones K se realiza con carácter global, asumiendo la estacionaridad de la función $K(h)$. No obstante, puede adaptarse a un uso local, considerando en lugar de una serie de puntos aleatorios, un punto concreto $i$. La expresión \ref{Eq:Ripley_estimador} puede particularizarse para dar un estimador de esta función K local, según

\begin{equation} \label{Eq:Ripley_estimador_local} \hat{K}(h) = \frac{1}{\lambda^2 A}\sum_{j=1, j\neq i}^N \frac{I_h(d_{ij})}{w_{ij}} \end{equation}

Autocorrelación espacial

Como vimos en Autocorrelacion_espacial , la autocorrelación espacial indica la relación entre el valor de una variable existente en un punto dado y los de la misma variable en el entorno cercano de dicho punto. La autocorrelación espacial es la expresión formal de la primera ley geográfica de Tobler, y puede ser tanto positiva (los puntos cercanos exhiben valores más similares que los puntos lejanos) o negativa (los puntos lejanos exhiben valores más similares que los puntos cercanos).

El desarrollo realizado entonces se centraba en tratar las implicaciones que la existencia de autocorrelación espacial tiene para el análisis estadístico de datos espaciales. En este apartado veremos índices que permiten evaluar el grado de autocorrelación espacial existente, así como elementos mediante los cuales dicha autocorrelación podrá utilizarse posteriormente como parte integrante de otras formulaciones, en particular las relacionadas con interpolación (Capítulo Creacion_capas_raster ).

La matriz de ponderación espacial

El concepto de autocorrelación espacial implica la definición de una vecindad de los distintos elementos geográficos. Se tiene que los valores de una variable registrados en aquellos elementos vecinos ejercen una influencia sobre los valores de dicha variable en un punto dado. Por ello es importante definir cuándo dos elementos son vecinos o no.

Aunque trabajamos con datos puntuales, este concepto de vecindad puede asociarse a otro tipo de entidades, como por ejemplo las de área. Así, puede considerarse que dos polígonos son vecinos si comparten al menos un lado común o, más restrictivamente, si comparten una longitud de sus perímetros mayor que un determinado umbral.

Para el caso de puntos, esta vecindad puede establecerse por distancia, considerando vecinos a todos aquellos puntos a una distancia menor que un umbral establecido. Este umbral puede aplicarse en todas direcciones (isotropía) o ser variable en función de la dirección (anisotropía).

De forma general, pueden considerarse todos aquellos factores que hagan que una entidad ejerza influencia sobre otra, y en el grado en la que dicha influencia tenga lugar. Esto puede incluir la consideración de otras relaciones existentes, como por ejemplo movimientos migratorios de especies, que «enlazan» unas entidades con otras y causan la existencia de interacción entre ellas más allá de la propia existente por distancia o contigüidad [ Anselin1992NCGIA ].

En la función K de Ripley ya vimos en la ecuación \ref{Eq:Ripley} cómo el uso del indicador $I$ definía ese concepto de vecindad «efectiva», ya que tomaba valor cero para los puntos a una distancia mayor que $h$, haciendo que dichos puntos no tuvieran efecto sobre el resultado final de la función. De forma similar, puede extenderse el concepto de este indicador para construir la denominada matriz de ponderación espacial .

Para un conjunto de $N$ entidades se tiene una matriz $W$ de dimensiones $N \times N$ en la que el elemento $w_{ij}$ refleja la influencia de la entidad $i$ sobre la $j$. Por convención, los valores $w_{ii}$ son iguales a cero. En el caso más sencillo, la matriz es de tipo binario, conteniendo únicamente valores 1 (existe vecindad efectiva entre las entidades) o 0 (no existe vecindad), pero los valores pueden ser cualesquiera. En la práctica, es de hecho habitual dividir estos valores por la suma de todos los valores de la columna, de forma que estén acotados siempre entre 0 y 1.

Mas allá de los valores que pueda contener, una característica primordial de la matriz de ponderación espacial es el método con el que ha sido creada, ya que la forma en la que se establece la vecindad entre los distintos elementos tiene influencia directa sobre dicha matriz. Esto, sin duda, afecta a las operaciones realizadas posteriormente sobre esta, por lo que la elección del método a emplear en su creación es altamente relevante.

Medidas de autocorrelación espacial

Dos son las medidas más habituales para cuantificar la autocorrelación espacial de una variable: el parámetro $I$ de Moran [ Moran1948JRSS ] y el parámetro $c$ de Geary [ Geary1954Incorporated ]. Ambos hacen uso de la matriz de ponderación espacial antes descrita.

En el caso del parámetro $I$ de Moran, su expresión es

\begin{equation} I = \frac{N}{S_0} \sum_{i=1}^N\sum_{j=1}^N \frac{w_{ij}(x_i-\mu)(x_j-\mu)}{\sum_{i=1}^N (x_i - \mu)^2} \end{equation}

donde $\mu$ es la media de la variable $x$ y $S_0$ es un factor de normalización igual a la suma de todos los elementos de la matriz.

\begin{equation} S_0 = \sum_{i=1}^N\sum_{j=1}^N w_{ij} \end{equation}

Si los valores de la matriz han sido normalizados dividiéndolos por la suma de las columnas, $S_0 = N$ y la expresión anterior se simplifica.

\begin{equation} I^* = \sum_{i=1}^N\sum_{j=1}^N \frac{w_{ij}(x_i-\mu)(x_j-\mu)}{\sum_{i=1}^N (x_i - \mu)^2} \end{equation}

El valor esperado de I es:

\begin{equation} E(I) = \frac{-1}{N-1} \end{equation}

Valores por debajo de este valor esperado indican autocorrelación negativa, mientras que los situados por encima reflejan autocorrelación positiva. Al igual que sucede para otros parámetros, los valores de la desviación típica del parámetro $I$ son conocidos, lo que permite establecer intervalos de confianza para rechazar o aceptar la hipótesis nula de ausencia de autocorrelación espacial.

Estos valores de la desviación típica tienen distintas expresiones en función de bajo qué supuestos se determinen. Estos supuestos y las expresiones resultantes no se tratarán aquí, pero pueden consultarse, por ejemplo, en [ Cliff1973Pion ].

Respecto el parámetro $c$ de Geary, su expresión es

\begin{equation} c = \frac{N-1}{2S_0} \sum_{i=1}^N\sum_{j=1}^N \frac{w_{ij}(x_i-x_j)^2}{\sum_{i=1}^N (x_i - \mu)^2} \end{equation}

Mientras que el parámetro $I$ da una caracterización más global, el parámetro $c$ es más sensible a las variaciones locales a distancia reducida.

El valor esperado de $c$ es 1. Valores menores de 1 indican autocorrelación espacial positiva, mientras que los superiores indican una autocorrelación negativa.

Ambos parámetros son parte de una familia de estadísticos denotadas como $\Gamma$, de la forma

\begin{equation} \Gamma = \sum_{i=1}^N\sum_{j=1}^N a_{ij}b_{ij} \end{equation}

Con este esquema pueden expresarse otros indicadores tales como los denominados índices de conteo conjunto ( joint count ) [ Cliff1973Pion ] u otros más específicos.

Todos estos parámetros caracterizan la autocorrelación espacial para el conjunto completo de puntos, es decir, para todo el área de estudio. Junto a estos, existen otros parámetros que miden la autocorrelación espacial a nivel local.

[ Getis1992GeoAnal ] proponen dos nuevos parámetros $G_i(d)$ y $G^*_i(d)$ que cuantifican si un punto dado $i$ se encuentra rodeado por agrupaciones de puntos con valores altos o bajos. En el caso de $G_i(d)$ no se tiene en cuenta el valor del punto $i$ mientras que en el caso de $G^*_i(d)$ sí se emplea este.

De forma similar, [ Anselin1995GeoAnal ] propone una versión local del parámetro $I$ de Moran, denotándolo como indicador local de asociación espacial ( Local Indicator of Spatial Association , LISA).

La forma de interpretar estos parámetros locales es similar a lo visto anteriormente, y las formulaciones concretas de cada uno pueden consultarse en las referencias correspondientes.

Variogramas

Los variogramas son elementos clave para definir la autocorrelación espacial y aprovechar el conocimiento de esta dentro de formulaciones como el kriging (ver Kriging ). Los variogramas se fundamentan en el concepto de semivarianza.

La semivarianza es una medida de la autocorrelación espacial de una variable $x$ entre dos puntos $i,j$, y viene expresada por

\begin{equation} \label{Eq:Semivarianza} \gamma(x_i,x_j) = \frac12(z_i-z_j)^2 \end{equation}

El cuadrado de las varianzas se multiplica por $\frac12$ debido a que $\gamma(x_i,x_j) = \gamma(x_j,x_i)$. De ahí el uso del prefijo semi .

Puesto que puede calcularse la distancia entre dichos puntos, pueden representarse los valores de $\gamma$ frente a las distancias $h$. Se obtiene una nube de puntos (nube del variograma) como la mostrada en la figura \ref{Fig:Nube_variograma}.

Representación de valores de semivarianza frente a distancia, formando la nube del variograma.

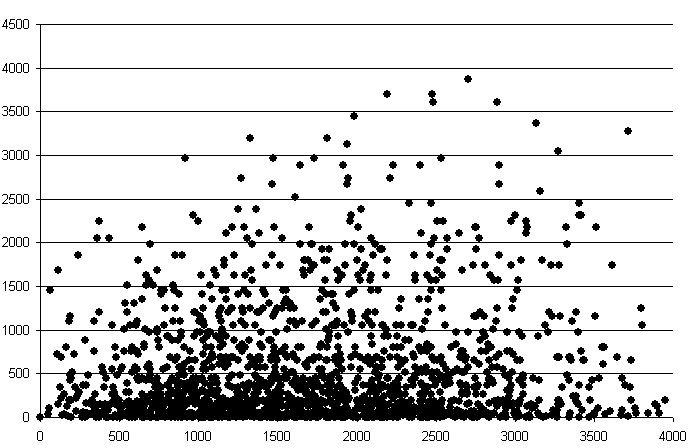
Esta nube aporta en principio poca información, pero puede resumirse agrupando los pares de puntos por intervalos de distancia, y calculando la media de todas las semivarianzas en cada intervalo. De esta forma se tiene una función que relaciona la semivarianza y la distancia entre puntos, según

\begin{equation} \gamma(h) = \frac1{2m-(h)}\sum_{i=1}^{m(h)} (x_i - x_j)^2 \end{equation}

siendo $m(h)$ el número de puntos del conjunto separados entre sí por una distancia $h$.

En la práctica se establecen una serie de valores de distancia equiespaciados, cada uno de los cuales define un intervalo centrado en dicho valor. La función $m(h)$ representa el número de puntos en cada bloque. Es importante que este número de puntos en cada bloque sea significativo, especialmente para dar validez al posterior ajuste sobre estos valores medios, como más adelante veremos.

La función $\gamma(h)$ es lo que se conoce como variograma experimental .

La nube de puntos de la figura \ref{Fig:Nube_variograma} se resume en el variograma de la figura \ref{Fig:Variograma}.

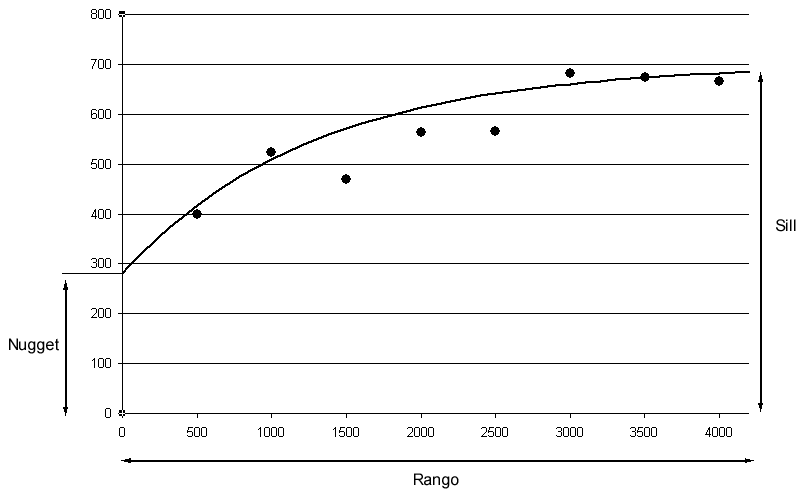
Resumen de la nube del variograma en un variograma experimental.

La elección de un tamaño óptimo para los intervalos es importante para obtener un variograma fiable. Si en el variograma aparecen ondulaciones, esto puede ser señal de que existe un comportamiento cíclico de la variable, pero más probablemente de que la distancia del intervalo no ha sido bien escogida.

Como puede verse en la figura, la curva que los puntos del variograma experimental describen implícitamente da lugar a la definición de unos elementos básicos que lo caracterizan.

Rango . El rango representa la máxima distancia a partir de la cual existe dependencia espacial. Es el valor en el que se alcanza la máxima varianza, o a partir del cual ya presenta una tendencia asintótica.
Sill . El máximo del variograma. Representa la máxima variabilidad en ausencia de dependencia espacial.
Nugget . Conforme la distancia tiende a cero, el valor de la semivarianza tiende a este valor. Representa una variabilidad que no puede explicarse mediante la estructura espacial.

Por ejemplo, para el caso de la figura propuesta estos valores pueden estimarse aproximadamente a primera vista como rango $\simeq$ 3000, sill $\simeq$ 700 y nugget $\simeq$ 300.

Puesto que existen procesos para los cuales la variación de valores no se da igual en todas las direcciones, existen también variogramas anisotrópicos que no solo indican la variación media dentro de un intervalo de distancia, sino que caracterizan esa variación para una distancia y una dirección concreta.

Una forma de visualizar cómo la variación es distinta en función de la dirección considerada es a través de una superficie variográficas . Estas superficies no son mapas como tales (la superficie variográfica a partir de una capa ráster no tiene las mismas coordenadas que esta. De hecho, no tiene coordenadas absolutas en el espacio), sino que, respecto a un punto central en el cual la variación es lógicamente cero, expresan en cada celda el valor medio que se da a la distancia y dirección que dicha celda define respecto al punto central.

Si se traza un perfil de valores de esta superficie desde el punto central hasta un extremo de esta y en una dirección dada, el conjunto de dichos valores conforma el variograma particular de esa dirección.

A partir de los puntos que forman el variograma experimental, puede definirse un modelo que aporta información sobre el proceso subyacente, a partir de su forma y sus parámetros. La definición de este modelo implica el ajuste de una curva a los puntos del variograma experimental, y tiene como resultado la obtención de un variograma teórico . En la figura \ref{Fig:Variograma} puede verse junto a los puntos del variograma experimental una curva ajustada a estos que define el variograma teórico. Sobre este último se pueden conocer las semivarianzas para cualquier distancia $h$, no solo para las definidas por los intervalos como en el caso del variograma experimental.

Existen muchas alternativas para elegir una función para el variograma teórico. Una función apta para este propósito debe cumplir los siguientes requisitos:

Ser monótona creciente.
Tener un máximo constante o asintótico. Es decir, un valor definido del sill . Funciones no acotadas superiormente, tales como las exponenciales, indicarían que la zona de estudio no es suficientemente grande, ya que no alcanza la dimensión a partir de la cual el efecto de la dependencia espacial deja de existir.
$\gamma(0)> 0$. Es decir, el nugget debe ser positivo.

Sobre la base anterior, se pueden establecer familias principales de funciones aptas para definir un variograma teórico:

Nugget puro. Funciones constantes de la forma \begin{equation} \gamma(h) =C_0 \qquad; \qquad \forall h \gt 0 \end{equation}
Funciones que alcanzan el valor del sill $(c)$ para un rango concreto $(a)$. Son funciones de la forma \begin{equation} \gamma(h) = \left\{ \begin{array}{ll} f(x) & \textrm{si $h \leq a$}\\ c & \textrm{si $h \gt a$} \end{array} \right. \end{equation} siendo las más habituales de las funciones $f(x)$ las de tipo lineal, circular o esférico. Las formulas detalladas de estas y otras funciones pueden consultarse, por ejemplo en [ Isaaks1989Oxford ].
Funciones que tienden asintóticamente al valor del sill $(c)$. Se define un rango efectivo , siendo este en el cual se da $\gamma(h) = 0.95c$. Entre estas funciones destacan
Exponencial

\begin{equation} \gamma(h) = c\left(1-e^{\frac{-3h}a}\right) \end{equation}

Gaussiana

\begin{equation} \gamma(h) = c\left(1-e^{\frac{-9h^2}{a^2}}\right) \end{equation}

Algunos autores como [ Goovaerts1997Oxford ] usan $h$ directamente en lugar de $3h$, en cuyo caso el rango no es igual a $a$, sino a $\frac{a}3$

El empleo de uno u otro modelo dependerá del conocimiento que tengamos acerca del proceso modelizado.

La figura \ref{Fig:Variogramas} muestra las gráficas de los tipos de variogramas anteriores.

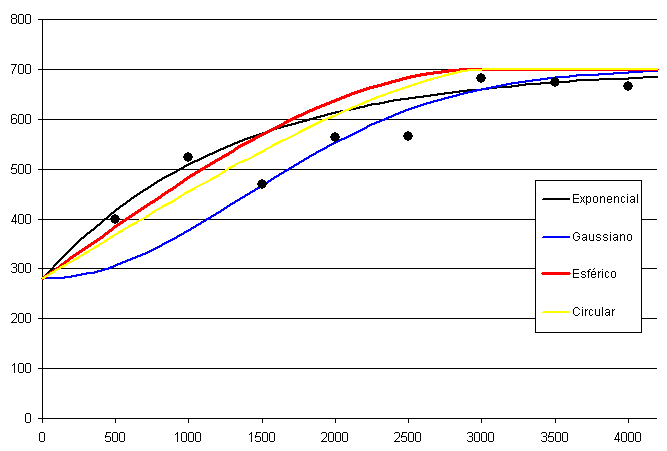
Distintos modelos de variograma teórico con los mismos parámetros de forma.

Llevar a cabo el ajuste del variograma teórico no es en absoluto un proceso trivial. Lo más sencillo es tratar de minimizar el error cuadrático. No obstante, deben tenerse en cuenta algunas consideraciones adicionales como las siguientes:

No todos los puntos del variograma experimental son igual de precisos. Si en un intervalo solo había cinco puntos en la nube del variograma mientras que en otro había 50, debe favorecerse un ajuste correcto sobre este último antes que sobre el primero, ya que su precisión será mayor.
Los puntos para valores altos del espaciamiento $h$ son menos relevantes y debe darse más importancia en el ajuste a los relativos a valores bajos. Esto se debe a que el objeto del variograma es modelizar la influencia que ejercen los puntos cercanos, y más allá del valor del rango esa influencia no se da, con lo que no es una parte de interés del variograma. Asimismo, la aplicación del kriging se realiza utilizando la parte inicial del variograma (valores pequeños de $h$), especialmente cuando hay una gran densidad de datos, por lo que resulta más apropiado tratar de minimizar los errores en esta parte inicial.

Una solución para incorporar lo anterior es, en lugar de minimizar el error cuadrático total, minimizar este ponderado según el número de puntos en cada intervalo y las distancias de estos. Es decir, minimizar

\begin{equation} \sum_{i=1}^b \frac{N_i}{h_i} (\hat{\gamma}(h_i)- \gamma(h_i))^2 \end{equation}

siendo $b$ el número de intervalos, $\hat{\gamma}(h_i)$ el valor en el variograma experimental y $\gamma(h_i)$ el valor en el variograma teórico.

La inspección visual del ajuste es también importante y resulta conveniente llevarla a cabo.

Por último, es importante señalar que el número total de puntos considerados debe tenerse en cuenta para saber si el variograma teórico calculado es fiable o no. Aunque resulta imposible establecer fórmulas exactas al respecto, se acepta generalmente que con menos de 50 puntos la fiabilidad del variograma será dudosa. Valores entre 100 y 150 son adecuados, y mayores de 250 puntos garantizan un variograma fiable.

En el caso de tratarse de variogramas anisotrópicos, estos números son mayores.

Correlogramas

Para dos variables independientes $x$ e $y$ dadas, se define la covarianza de una muestra como

\begin{equation} S_{xy}=\frac{1}{n-1}\sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y}) \end{equation}

Puede aplicarse este concepto para una única variable dada. Para dos puntos dados, su covarianza es

\begin{equation} S_{ij} = (x_i - \overline{x}) (x_j - \overline{y}) \end{equation}

El conjunto de valores de covarianza y distancias entre puntos da lugar a una nube de valores que, al igual que ocurría con las semivarianzas, puede emplearse para crear una curva experimental y a partir de esta una curva teórica. Con dicha curva teórica se tiene conocimiento de la covarianza a cualquier distancia, y recibe el nombre de correlograma .

Existe una relación directa entre el variograma y el correlagrama, como puede verse en la figura \ref{Fig:Variograma_correlograma}.

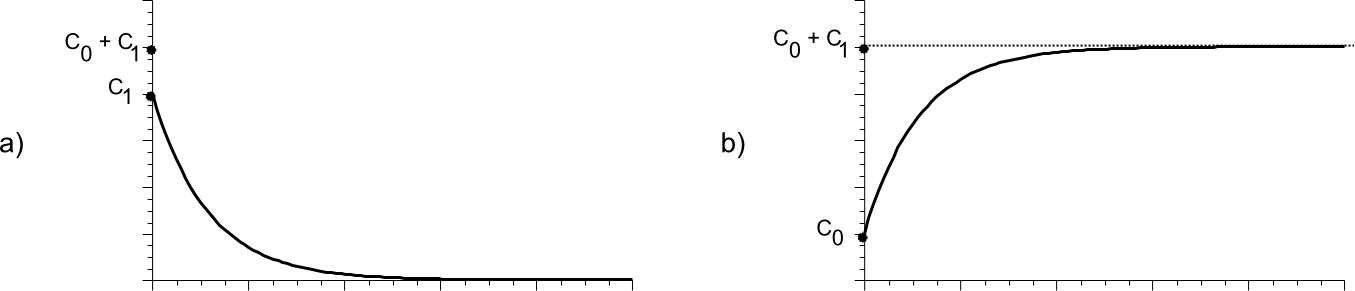
Relación entre correlograma (a) y variograma (b)

Con la notación de la figura, se tiene para el caso del variograma que

\begin{eqnarray} \gamma(h) = \left\{ \begin{array}{ll} 0 & \textrm{si $\|h\| = 0$}\\ C_0 + C_1\left(1-e^{h/a}\right) & \textrm{si $\|h\| > a$} \end{array} \right. \nonumber \end{eqnarray}

Para el correlograma, se tiene que

\begin{eqnarray} \gamma(h) = \left\{ \begin{array}{ll} C_0 + C_1 & \textrm{si $\|h\| = 0$}\\ C_1\left(e^{h/a}\right) & \textrm{si $\|h\| > a$} \end{array} \right. \end{eqnarray}

En la práctica, se emplea el variograma porque resulta más sencillo modelizar las semivarianzas que las covarianzas.

Resumen

Los datos espaciales presentan particularidades que deben considerarse a la hora de realizar cálculos estadísticos sobre ellos.Teniendo esto en cuenta, existen muy diversas formas llevar a cabo el análisis estadístico de datos espaciales, de las cuales hemos visto algunas de las más importantes.

Los elementos básicos de estadística descriptiva para datos espaciales son el centro medio, el centro mediano y la distancia típica. La elipse de variación permite representar gráficamente la dispersión, considerando que esta no se da igual en todas direcciones.

En el caso de trabajar con líneas y las direcciones que estas definen, es importante tener en cuenta la naturaleza circular de las variables. El trabajo con vectores en lugar de valores escalares es una solución práctica habitual para evitar resultados incorrectos.

Otro elemento importante del análisis estadístico espacial es el análisis de patrones de puntos. El método de división por cuadrantes, el de vecino más cercano, o el basado en funciones K de Ripley, todos ellos permiten caracterizar la disposición espacial de los puntos y con ello el proceso puntual inherente que da lugar a la misma.

Por último, la existencia de autocorrelación espacial puede medirse con índices como el $I$ de Moran o el $c$ de Geary, así como analizarse a través de variogramas. A partir de los datos de las semivarianzas se elabora un variograma experimental, el cual sirve como base para el ajuste de un variograma teórico. Este puede puede emplearse posteriormente en otras técnicas tales como el kriging, que veremos más adelante.