Creación de capas ráster

Introducción

Una buena parte de los análisis geográficos se realizan sobre capas ráster. Estas, por sus propias características, se prestan mejor a cierto tipo de análisis, y la implementación de estos resulta más sencilla, por lo que lo habitual es encontrarlos implementados para ser empleados con capas de esta clase.

La información de la que disponemos no siempre se encuentra en este formato, pero ello no significa que no podamos utilizarla. A partir de información almacenada según otros modelos de datos, podemos generar capas ráster (este proceso lo denominaremos rasterización ) que reúnan las características necesarias para usarse con los algoritmos correspondientes. El problema es en todos los casos la creación de una estructura regular a partir de información que no es regular, tal como la contenida en un TIN, una capa de polígonos, una de líneas, o una capa de valores puntuales.

Si disponemos de una capa de polígonos y estos cubren la totalidad del territorio, este proceso no es difícil. Basta ver dentro de qué polígono cae la coordenada que define cada celda, y asignar a esta el valor de uno de los atributos de la capa de polígonos, el cual contenga la variable a recoger en la capa ráster. En el caso del TIN es similar, ya que cada uno de los triángulos permite el cálculo de valores en sus puntos, y puede igualmente establecerse una relación entre estos y las celdas de una malla ráster que cubra el mismo espacio geográfico.

Si tenemos una capa de líneas la cosa no es muy distinta. Basta ver por qué celdas pasan esas líneas y asignar el valor de estas a dichas celdas. Pueden existir ambigüedades a la hora de considerar cuánto ha de recorrer una línea a través de una celda para considerar que pasa por esta y asignarle el valor correspondientes, como se muestra en la figura \ref{Fig:Formas_rasterizacion_lineas}. Aun así, y salvando estos aspectos, no resulta difícil rasterizar una capa de líneas y tener una capa ráster válida.

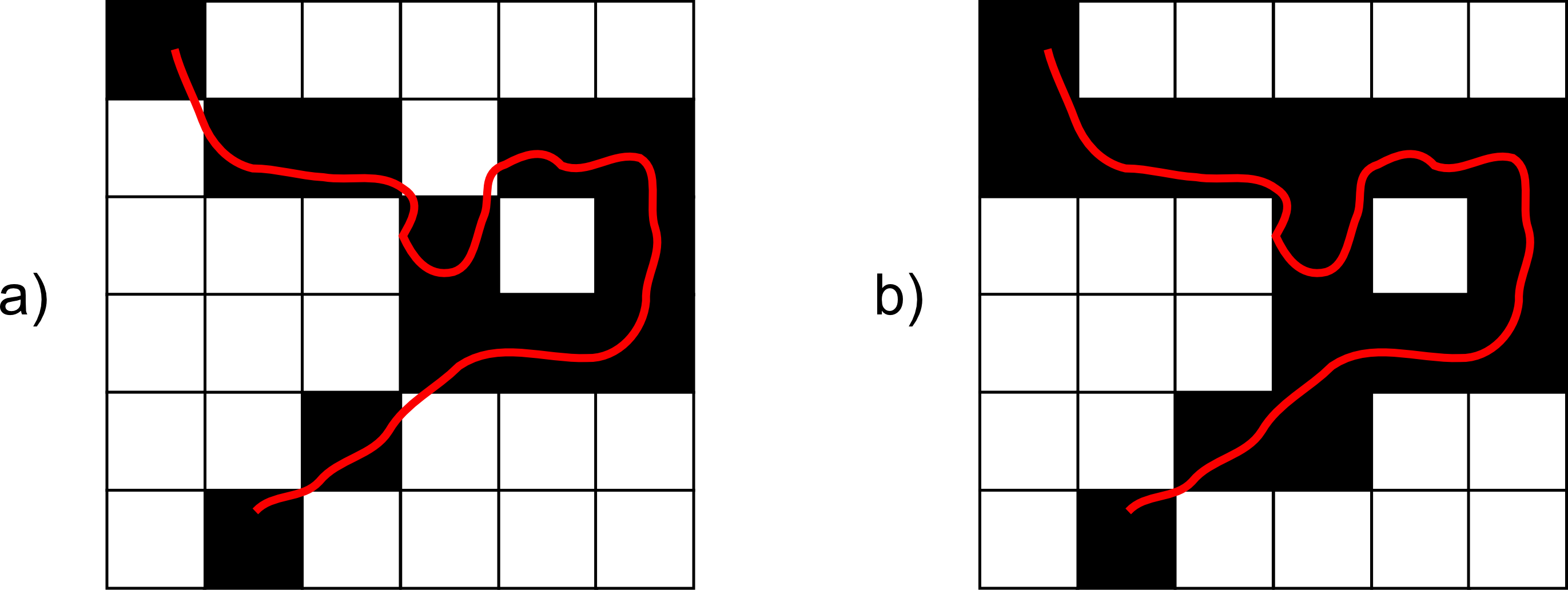
Formas distintas de rasterizar una línea en función del criterio empleado.

Por último, para el caso de una capa de puntos, la conversión en una capa ráster es aún más sencilla. Basta con asignar los correspondientes valores a aquellas celdas en las que se sitúen los puntos. Las restantes, y puesto que no existe información al respecto, deberán llevar el valor que codifica la ausencia de datos.

Estas formas de rasterización, sin embargo, pueden no ser idóneas según las circunstancias. En los dos últimos casos (líneas y puntos), y especialmente para el caso de puntos, la situación que se recoge en la capa ráster puede no ser la necesaria para el análisis, y realmente no estaremos aprovechando las capacidades del modelo de datos ráster a pesar de haber llevado a cabo una conversión.

Por ejemplo, si las líneas que rasterizamos son curvas de nivel, van a indicar la elevación en las mismas. Fuera de ellas, la capa ráster generada no tendrá datos, pero en realidad esas celdas sí que tienen una elevación concreta. Del mismo modo sucede si medimos esa elevación en una serie de puntos en lugar de en líneas y después rasterizamos la capa, o si medimos cualquier otra variable en un número dado de localizaciones puntuales y hacemos lo propio.

Para aprovechar la buena disposición del modelo ráster para el análisis, y especialmente en el caso de variables continuas, debemos tener una capa que contenga información en todas sus celdas, incluso si originalmente solo hemos medido los valores de la variable estudiada en una serie de celdas. Será en base a los valores de esas celdas como obtengamos posteriormente los valores en las restantes.

Los métodos de interpolación que veremos en este capítulo permiten rellenar esas celdas restantes a partir de los valores puntuales conocidos, realizando estimaciones. Para ello, aplican conceptos de estadística espacial más o menos complejos según su formulación particular, de tal modo que los puntos cercanos a cada celda son los que determinan el valor estimado de esta. Este hecho es una aplicación directa de la ley de Tobler, que establece que los puntos cercanos tiene mayor probabilidad de tener valores similares que aquellos separados por una distancia mayor.

En términos generales, un método de interpolación es una herramienta que permite el cálculo del valor de una variable en una coordenada para la cual dicho valor no es conocido, a partir de los valores conocidos para otra serie de coordenadas. En el caso particular de la creación de una capa ráster, las coordenadas $(x,y)$ donde han de calcularse los valores desconocidos son los centros de las celdas sin dato recogido.

El número de métodos distintos es muy amplio, y es importante reseñar que la bondad o no de uno u otro va ligada no solo al método en sí, sino también a la variable interpolada y al uso que se dé posteriormente a la capa resultante.

La aplicación de los métodos de interpolación es, asimismo, muy diversa. Casos habituales son, por ejemplo, la realizada a partir de datos de elevación tomados en campo mediante GPS o estación total, o de los datos climatológicos de precipitación y temperatura registrados en los observatorios de una red. Resulta imposible recoger valores para cada una de las celdas de una capa ráster que cubra el territorio a estudiar, pero estas variables, por ser continuas, se manejarán mejor y serán más útiles si se dispone de ellas en formato ráster. Los métodos de interpolación son los encargados de convertir esos datos puntuales en mallas regulares.

Tres situaciones para la aplicación de interpolación espacial.

En general, cualquier variable recogida mediante muestreo puede ser el punto de partida para la aplicación de dichos métodos.

En algunos de los casos anteriores, los valores en las celdas guardan una dependencia no solo con los puntos que contienen la variable interpolada, sino también con otras variables de las que puede o no disponerse de información. Por ejemplo, para el caso de la temperatura, esta se encuentra influenciada por la elevación. De igual modo, las características del suelo tendrán relación con parámetros del relieve tales como la pendiente o índices relacionados con la humedad topográfica (Capítulo Geomorfometria ).

Estas variables, que denominamos variables de apoyo o predictores , puede incorporarse como datos de partida a algunos métodos de interpolación, aumentando así su precisión. En general, se requiere que dichas variables de apoyo estén recogidas en formato ráster. Asimismo, pueden plantearse análisis de regresión mediante los cuales, y sin necesidad de utilizar la componente espacial, puedan estimarse los valores en las celdas problema a partir de los valores de la variable en los puntos conocidos y los valores de los predictores tanto en dichos puntos como en las celdas a rellenar.

Junto con lo anterior, la información de una determinada variable cuantitativa tomada en ciertos puntos puede servir para estimar densidades de dicha variable (tales como, por ejemplo, individuos de una especie) y crear superficies continuas. Este análisis se lleva a cabo no con métodos de interpolación o regresión, sino con otra serie de algoritmos habituales en los SIG que veremos al final del capítulo.

Interpolación

Un método de interpolación permite el calculo de valores en puntos no muestreados, a partir de los valores recogidos en otra serie de puntos.

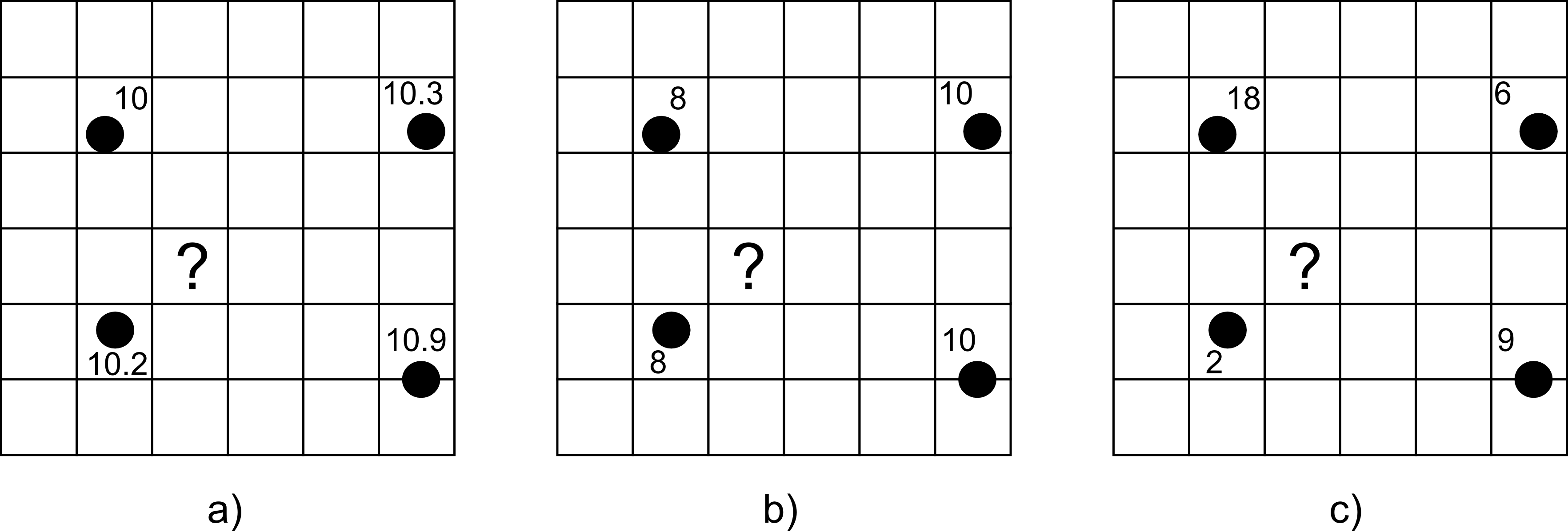
En la figura \ref{Fig:EjInterpolacion} encontramos tres situaciones en las cuales se hace necesario el uso de interpolación si queremos obtener una capa raster con valores en todas sus celdas. En dichas situaciones, los cuatro puntos señalados han sido muestreados y se dispone de un valor en ellos. Adviértase que no han de encontrarse necesariamente en el centro de las celdas. El problema es el mismo en cada uno de estos supuestos: queremos estimar los valores en las celdas de la malla, y en particular en la celda marcada con un interrogante.

Para el caso a) la lógica nos indica que el valor en esta celda debe estar alrededor de 10, ya que este valor sigue la tendencia natural de los valores recogidos, que tiene todos ellos un valor de esa magnitud. Si aplicamos cualquiera de los métodos de interpolación que veremos a continuación, el valor que obtengamos será con seguridad muy aproximado a esa cifra.

Supongamos ahora que nos encontramos en el caso b). En este supuesto, la lógica nos indica que el valor será inferior a 10, y también probablemente a la media de los valores muestrales (9), ya que la celda problema se sitúa más cerca de los valores inferiores que de los superiores a ese valor medio. Razonando de este modo, aplicamos el hecho de que la proximidad incrementa la semejanza de valores. Es decir, que existe autocorrelación espacial para la variable interpolada.

El caso c) es algo distinto. Aquí ya no parece tan sencillo «adivinar» el valor que corresponde. Esto es así no porque las operaciones sean más complejas, sino porque no existe de la misma forma que en los ejemplos anteriores la autocorrelación espacial de la variable, y esa lógica no resulta tan obvia. Utilizando los distintos métodos de interpolación, puede ser que estos den valores distintos, ya que se comportarán de forma diferente ante tal situación.

Estos sencillos ejemplos numéricos tienen como objetivo dar imagen general de lo que el proceso de interpolación conlleva, y que puede resultar más intuitivo al analizarlo sobre un conjunto reducido de puntos. A pesar de sus diferencias, grandes en muchos casos, todos parten de ideas comunes que lo único que pretenden es replicar de forma lo más precisa posible un campo a partir de un conjunto definido de puntos con valores de este.

Existen muchos métodos de interpolación, de los cuales algunos cuentan con más presencia en los SIG por estar más adaptados al tipo de dato que se maneja. Su aplicación habitual dentro de un SIG es bidimensional, ya que una capa ráster es una entidad bidimensional. Hablamos, por ello, de interpolación espacial . No obstante, estos métodos no han de restringirse al plano, y pueden extenderse a un numero superior de dimensiones para reflejar otras variables tales como la profundidad (por ejemplo, para construir un modelo tridimensional de las características del suelo entre dos profundidades establecidas y con un intervalo dado), o bien el tiempo.

Podemos clasificar los distintos métodos de interpolación según varios criterios [ Burrough1986Oxford ].

Según los puntos considerados para el cálculo de valores . Algunos métodos consideran que todos los puntos de los que disponemos tienen influencia sobre el valor a calcular en una celda. Estos modelos se conocen como globales . En otros, denominados locales , solo se considera un conjunto restringido de estos. Este conjunto puede establecerse por medio de un umbral de distancia (todos los situados a una distancia menor que el umbral), de conteo (los $n$ puntos más cercanos), o bien ambos.
La selección de este conjunto de puntos más cercanos (los de más influencia) es un aspecto importante en el rendimiento de los métodos de interpolación de este tipo. Cuando se trabaja con un número de puntos elevado, se hace inviable el cálculo de las distancias entre todos esos puntos para seleccionar los más cercanos. El uso de índices espaciales y otras estructuras semejantes (véase Indices_espaciales ) se hace necesario para poder aplicar eficientemente estos métodos de interpolación sobre dichos conjuntos con tal número de puntos.

En realidad, un método global puede entenderse como uno local con un umbral infinito, no existiendo una dicotomía estricta entre ambas clases.
Según su valor en los puntos de partida . En algunos métodos, denominados exactos , los valores asignados a las coordenadas correspondientes a los puntos de origen son exactamente los recogidos en dichos puntos. En los métodos aproximados , el valor en esas celdas es el que corresponde al mejor ajuste, y no ha de coincidir necesariamente con el valor original.
Según la inclusión o no de elementos probabilísticos . Diferenciamos entre métodos estocásticos (aquellos que emplean elementos probabilísticos) y métodos determinísticos (aquellos que no los emplean).

Por vecindad

El método más sencillo de interpolación es el de vecindad o vecino más cercano . En él se asigna directamente a cada celda el valor del punto más cercano. No existe formulación matemática que emplee las distancias entre puntos o los valores de estos, sino que el valor resultante es sencillamente el del punto más próximo.

Se trata, por tanto, de un método local, exacto y determinístico.

El resultado es una capa con saltos abruptos (tanto como lo sean las diferencias entre los valores de puntos cercanos), con un aspecto «aterrazado» (Figura \ref{Fig:Interpolacion_vecindad}). El conjunto de celdas con el mismo valor (dentro de la misma terraza) representa el lugar geométrico de las celdas cuyo punto más cercano de entre los de partida es uno dado.

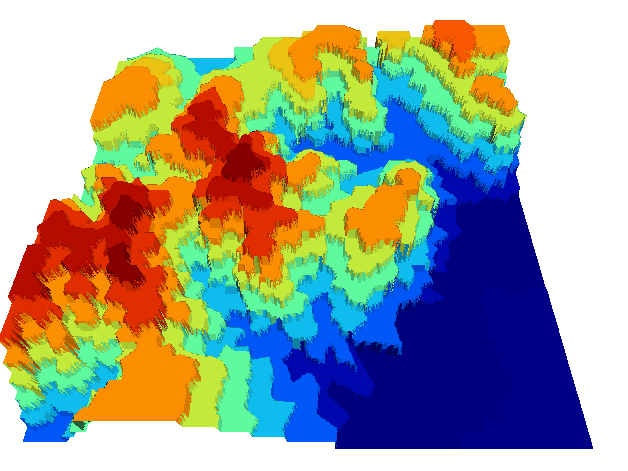
Superficie obtenida mediante interpolación por vecindad.

La interpolación por vecindad no es adecuada para el trabajo con variables continuas, pero sí para variables categóricas. Por ejemplo, para un conjunto de puntos cada uno de los cuales esté identificado con un código numérico, la interpolación por vecindad de ese valor da como resultado una capa donde los valores de las celdas identifican el punto más cercano. Esto puede utilizarse para calcular la influencia de cada uno de ellos en el espacio representado.

Este tipo de razonamientos ha sido empleado tradicionalmente para calcular los denominados polígonos de Thiessen , de uso habitual en el análisis climatológico, asociando a cada zona los valores de la estación meteorológica más cercana. Estos polígonos de Thiessen conforman una estructura conocida como teselación de Voronoi , que puede también calcularse de forma vectorial, como veremos en el capítulo Creacion_capas_vectoriales . La teselación de Voronoi está íntimamente ligada a la denominada triangulación de Delaunay , base para la construcción de TIN como en su momento detallaremos.

Métodos basados en ponderación por distancia

Los métodos basados en ponderación por distancia son algoritmos de interpolación de tipo local, aproximados y determinísticos. El valor en una coordenada dada se calcula mediante una media ponderada de los puntos de influencia seleccionados (bien sea la selección por distancia o por número de estos). Su expresión es de la forma [ Shepard1968ACM ]

\begin{equation} \widehat{z}=\frac{\sum_{i=1}^n p_i z_i^k}{\sum_{i=1}^n p_i^k} \end{equation}

siendo $p_i$ el peso asignado al punto i-ésimo. Este peso puede ser cualquier función dependiente de la distancia.

La función más habitual es la que da lugar al método de ponderación por distancia inversa , de la forma

\begin{equation} \label{Eq:Distancia_inversa} p_i = \frac{1}{d_i^k} \end{equation}

donde el exponente $k$ toma habitualmente el valor 2.

Otra función habitual es la de la forma

\begin{equation} p_i = e^{-kd_i} \end{equation}

así como la que constituye el método de decremento lineal , con la siguiente expresión:

\begin{equation} \label{Eq:Decremento_lineal} p_i = 1 - (\frac{d_i}{d_{max}})^k \end{equation}

donde $k$ es un parámetro que regula la forma de la función y $d_{max}$ la distancia máxima de influencia.

La figura \ref{Fig:Interpolacion_distancia} muestra la superficie calculada a partir de datos puntuales de elevación aplicando el método de ponderación por distancia inversa.

Superficie obtenida mediante ponderación por distancia inversa

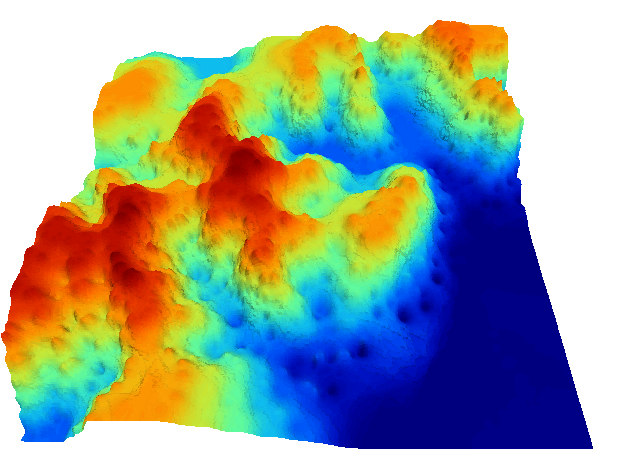
$$\label{Fig:Interpolacion_distancia}$$

Los métodos basados en ponderación por distancia solo tienen en cuenta el alejamiento, pero no la posición. Es decir, un punto situado a una distancia $d$ hacia el Norte tiene la misma influencia que uno situado a esa misma distancia $d$ pero hacia el Oeste.

Igualmente, los métodos basados en distancia no generan valores que se encuentren fuera del rango de valores de los datos de entrada. Eso causa efectos indeseados en caso de que el muestro de datos no recoja los puntos característicos de la superficie interpolada. La figura \ref{Fig:Zonas_llanas_por_IDW} muestra en un caso unidimensional cómo, de no recogerse los valores extremos (tales como cimas o valles), estos desaparecen y son sustituidos por tramos llanos

La interpolación basada en ponderación por distancia (a) no crea valores extremos si estos no han sido recogidos, lo cual deriva en un «aplanamiento» de la superficie y la aparición de falsas terrazas. Otros métodos tales como los *splines* (b) sí que permiten la aparición de valores fuera del rango muestreado.

Puede entenderse el método de vecino más cercano como un caso particular de método ponderado por distancia, en el que se emplea un único punto de influencia, y su peso asignado es $p_1=1$.

Curvas adaptativas (Splines)

Las curvas adaptativas o splines conforman una familia de métodos de interpolación exactos, determinísticos y locales. Desde un punto de vista físico pueden asemejarse a situar una superficie elástica sobre el área a interpolar, fijando esta sobre los puntos conocidos. Crean así superficies suaves, cuyas características pueden regularse modificando el tipo de curva empleada o los parámetros de esta, de la misma forma que sucedería si se variasen las cualidades de esa membrana ficticia.

La superficie creada cumple la condición de minimizar con carácter global alguna propiedad tal como la curvatura.

Desde un punto de vista matemático, los splines son funciones polinómicas por tramos, de tal modo que en lugar de emplear un único polinomio para ajustar a todo un intervalo, se emplea uno distinto de ellos para cada tramo. Las curvas definidas por estos polinomios se enlazan entre ellas en los denominados nudos , cumpliendo unas condiciones particulares de continuidad.

Los splines no sufren los principales defectos de los dos métodos anteriores. Por un lado, pueden alcanzar valores fuera del rango definido por los puntos de partida. Por otro, el mal comportamiento de las funciones polinómicas entre puntos se evita incluso al utilizar polinomios de grados elevados. No obstante, en zonas con cambios bruscos de valores (como por ejemplo, dos puntos de entrada cercanos pero con valores muy diferentes), pueden presentarse oscilaciones artificiales significativas. Para solucionar este problema, una solución es el empleo de splines con tensión [ Schweikert1966JMP ]. La incorporación de la tensión en una dirección permite añadir anisotropía al proceso de interpolación [ Mitasova1993MathGeo ].

Kriging

El kriging es un método de interpolación estocástico, exacto, aplicable tanto de forma global como local. Se trata de un método complejo con una fuerte carga (geo-)estadística, del que existen además diversas variantes.

El kriging se basa en la teoría de variables regionalizadas, la cual fue desarrollada por [ Matheron1963EcoGeo ] a partir del trabajo pionero de [ Krige1951MsC ]. El objetivo del método es ofrecer una forma objetiva de establecer la ponderación óptima entre los puntos en un interpolador local. Tal interpolación óptima debe cumplir los siguientes requisitos, que son cubiertos por el kriging:

El error de predicción debe ser mínimo.
Los puntos cercanos deben tener pesos mayores que los lejanos.
La presencia de un punto cercano en una dirección dada debe restar influencia (enmascarar) a puntos en la misma dirección pero más lejanos.
Puntos muy cercanos con valores muy similares deben «agruparse», de tal forma que no aparezca sesgo por sobremuestreo.
La estimación del error debe hacerse en función de la estructura de los puntos, no de los valores.

Junto con la superficie interpolada, el kriging genera asimismo superficies con medidas del error de interpolación, que pueden emplearse para conocer la bondad de esta en las distintas zonas.

En su expresión fundamental, el kriging es semejante a un método basado en ponderación por distancia. Dicha expresión es de la forma

\begin{equation} \label{Eq:Kriging} \widehat{z}=\sum_{i=1}^n z_i \Lambda_i \end{equation}

siendo $\Lambda_i$ los pesos asignados a cada uno de los puntos considerados. El cálculo de estos pesos, no obstante, se realiza de forma más compleja que en la ponderación por distancia, ya que en lugar de utilizar dichas distancias se acude al análisis de la autocorrelación a través del variograma teórico ( Variogramas ). Por ello se requiere, asimismo, que exista un número suficiente de puntos (mayor de 50, como se vio en el capítulo Estadistica_espacial ) para estimar correctamente el variograma.

A partir de los valores del variograma, se estima un vector de pesos que, multiplicado por el vector de valores de los puntos de influencia, da el valor estimado.

En el denominado kriging ordinario , e interpolando para un punto $p$ empleando $n$ puntos de influencia alrededor de este, el antedicho vector de pesos se calcula según

\begin{equation} \scriptsize \left( \begin{array}{c} w_1 \\ w_2 \\ \vdots \\ w_n\\ \lambda \end{array} \right) = \left( \begin{array}{cccc} \gamma(d_{11}) & \cdots & \gamma(d_{1n}) & 1 \\ \gamma(d_{21}) & \cdots & \gamma(d_{2n}) & 1\\ \vdots & \ddots & \vdots & 1\\ \gamma(d_{n1}) & \cdots & \gamma(d_{nn}) & 1\\ 1 & \cdots & 1 & 0 \\ \end{array} \right) \left(\begin{array}{c} \gamma(d_{1p}) \\ \gamma(d_{2p}) \\ \vdots \\ \gamma(d_{np})\\ 1\\ \end{array} \right) \end{equation}

siendo $d_{ij}$ la distancia entre los puntos $i$ y $j$, y $\lambda$ un multiplicador de Lagrange.

El error esperado en la estimación también se obtiene, como se dijo antes, a partir de la estructura de los puntos. Es decir, utilizando igualmente el variograma. Para ello se emplean los pesos calculados anteriormente, según

\begin{equation} S_p^2 = \sum_{i=1}^n w_i\gamma(d_{ip}) + \lambda \end{equation}

La aplicación del kriging ordinario implica la asunción de una serie de características de los datos:

Estacionaridad de primer y segundo orden. La media y la varianza son constantes a lo largo del área interpolada, y la covarianza depende únicamente de la distancia entre puntos.
Normalidad de la variable interpolada.
Existencia de una autocorrelación significativa.

La figura \ref{Fig:Interpolacion_kriging} muestra una superficie obtenida mediante kriging ordinario, junto a la capa de varianzas asociada.

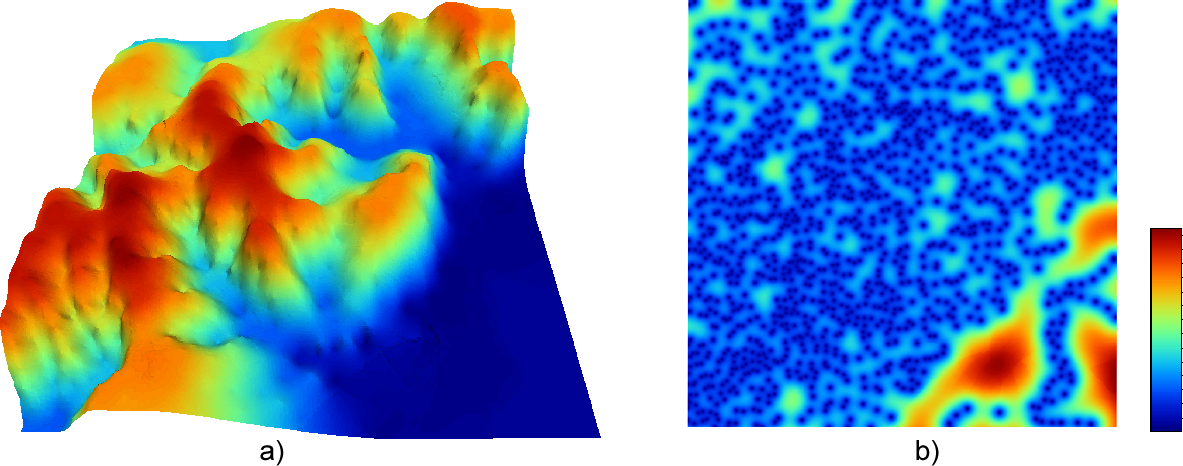
Superficie obtenida mediante interpolación por kriging ordinario y capa de varianzas.

Cuando no puede asumirse la estacionariedad de primer orden y existen una tendencia marcada en el valor medio esperado en los distintos puntos, puede aplicarse un tipo de kriging denominado kriging universal . Además de los valores a interpolar y sus coordenadas, este método permite el uso de predictores relacionados con dicha tendencia.

El kriging con regresión es similar en cuanto a sus resultados e ideas, aunque la forma de proceder es distinta. Mientras que en el universal se trabaja con los residuos y la superficie de tendencia conjuntamente, este separa ambas partes y las analiza por separado, combinándolas después para estimar los valores y los errores asociados.

Existen muchas otras variaciones del kriging tales como el kriging simple , el kriging por bloques o el co--kriging . La aplicación de estas formas, sin embargo, es limitada, debido a que no es tan frecuente su implementación. Los SIG habituales implementan por regla general las variantes básicas anteriores, quedando las restantes para programas especializados.

Ajuste de funciones. Superficies de tendencia

El ajuste de funciones es un método de interpolación determinístico o estocástico (según el tipo de función a ajustar), aproximado y global. Puede aplicarse de forma local, aunque esto resulta menos habitual. Dado el conjunto completo de los puntos de partida, se estima una superficie definida por una función de la forma

\begin{equation} \widehat{z} = f(x,y) \end{equation}

El ajuste de la función se realiza por mínimos cuadrados.

Estas funciones son de tipo polinómico, y permiten el cálculo de parámetros en todas las celdas de la capa ráster. Por su propia construcción, requieren pocas operaciones y son rápidos de calcular. Sin embargo, esta sencillez es también su principal inconveniente. Los polinomios de grado cero (plano constante), uno (plano inclinado), dos (colina o depresión) o tres, son todos ellos demasiado simples, y las variables continuas que pueden requerir un proceso de interpolación dentro de un SIG son por lo general mucho más complejas. Pueden emplearse polinomios de mayor grado que aumentan la precisión del ajuste en los puntos de partida. Sin embargo, aumenta por igual la oscilación de la función entre puntos, mostrando un mal comportamiento con grados elevados, y no obteniéndose en ningún caso la fidelidad a la superficie real que se logra con otros métodos.

La figura \ref{Fig:Interpolacion_funcion} muestra superficies con valores de elevación obtenidos mediante ajuste polinómico de grados dos y cinco.

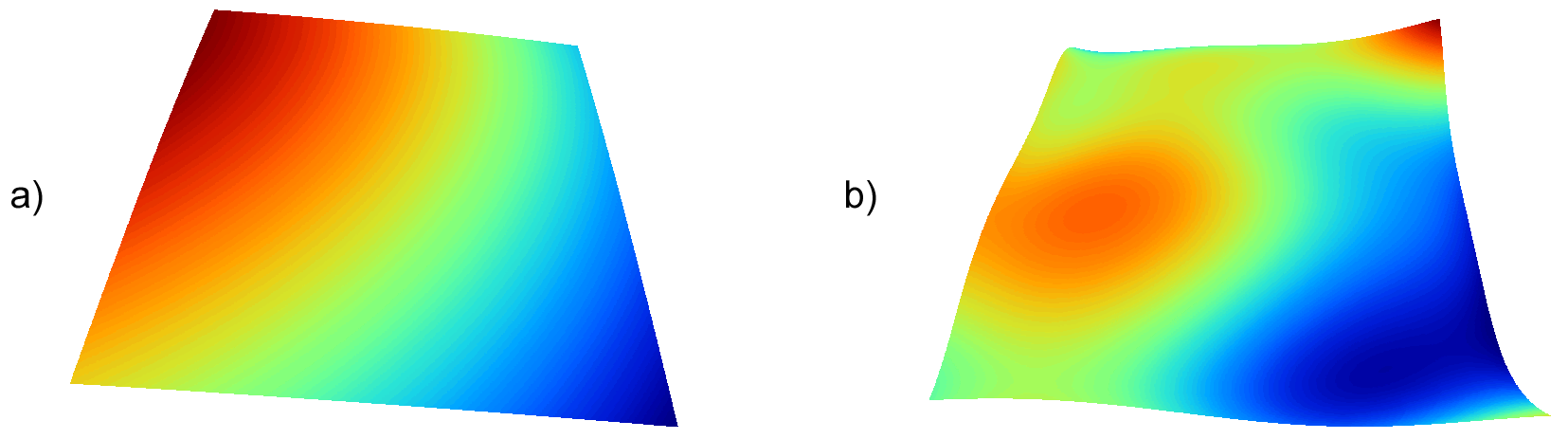
Superficies obtenidas mediante interpolación por ajuste polinómico de segundo (a) y quinto (b) grado.

El empleo de funciones de ajuste permite incorporar otras variables adicionales $h_i$ mediante funciones de la forma \begin{equation} \label{Eq:Ajuste_polinomios} \widehat{z} = f(x,y, h_1, …, h_n) \end{equation}

Esto posibilita la incorporación de variables de apoyo (predictores) que pueden tener una influencia en la variable interpolada, considerando así no únicamente la posición de los distintos puntos, sino los valores en ellos de dichas variables de apoyo.

Si bien en muchos casos la superficie interpolada puede no reflejar con precisión una variable, puede emplearse para considerar el efecto de tendencias globales en la distribución de esta. Una variable puede estar condicionada por efectos globales y efectos locales. Puesto que el ajuste de una función polinómica tal y como lo hemos visto aquí es un interpolador global, permite la separación de estos dos tipos de efectos. Este proceso constituye el empleo de las denominadas superficies de tendencia .

Supongamos una capa de temperatura. Esta dependerá de la altura, pero también de la latitud. Existe, por tanto, una tendencia global: a mayor latitud (supóngase hemisferio norte), menor temperatura. Esta se puede modelizar con una función lineal, y separar el efecto de ambos factores, altitud y latitud (Figura \ref{Fig:Superficies_tendencia}). El efecto local puede entenderse como el residuo de primer orden de la superficie interpolada.

Separación de una variable en un efecto debido a una tendencia geográfica (en este caso en forma de plano inclinado con valores mayores en la parte derecha) y un efecto local.

En la aplicación de predictores debe tenerse en cuenta el principio de parsimonia: mantener el modelo lo más simple posible. La incorporación de nuevos predictores, si estos se encuentran significativamente correlacionados, conlleva un aumento de la multicolinearidad [ Myers1990PWS ]. Esta circunstancia da lugar a un sobreajuste de la función y empeora la calidad de las estimaciones, especialmente en la predicción de datos fuera del área delimitada por los puntos de partida, es decir, la extrapolación.

Un caso particular de las funciones del tipo señalado en la ecuación \ref{Eq:Ajuste_polinomios} son las de la forma

\begin{equation} \widehat{z} = f(h_1, …, h_n) \end{equation}

es decir, aquellas que no consideran la componente geográfica y simplemente realizan una regresión en el espacio de atributos.

Puesto que existe autocorrelación espacial, en el caso de considerar el espacio geográfico resulta más conveniente el uso de mínimos cuadrados generalizados en lugar de mínimos cuadrados ordinarios. En el capítulo Estadistica_avanzada veremos con más detalle los temas relacionados con regresiones e inferencia estadística basada en datos espaciales.

Muestreo de datos para interpolación

Muchas veces, la información de la que disponemos la obtenemos de una fuente ajena y no queda más remedio que emplearla tal y como la recibimos. Tal es el caso de una curvas de nivel digitalizadas de un mapa clásico (no podemos disponer de más curvas porque no existen en el mapa original), o de unos datos de observatorios meteorológicos (no podemos densificar esa red y disponer de datos medidos en otros puntos).

En otras ocasiones, sin embargo, los datos pueden no haber sido tomados aún y debe plantearse un esquema para ello. Es decir, que ese conjunto finito de puntos a partir de los cuales obtener una superficie interpolada puede ser creado a voluntad, siempre que nos mantengamos dentro del marco de limitaciones (temporales, monetarias, etc.) existentes. El diseño del muestreo de forma eficiente ayuda de manera directa a obtener mejores resultados al interpolar los datos recogidos. Este diseño de muestreo puede realizarse no solo para obtener un conjunto de datos base, sino para enriquecer uno ya existente, ampliándolo con nuevos puntos.

El objetivo de un muestreo espacial es poder inferir nueva información acerca de una población en la que sus distintos elementos están georreferenciados, a partir de un subconjunto de dicha población. La razón de llevar a cabo el muestreo es la imposibilidad de analizar todos los miembros de la población, ya que estos pueden ser muy numerosos (como en el caso de todos los habitantes de un país) o infinitos (como sucede para variables continuas tales como elevaciones o temperaturas).

Aunque el uso de un muestreo no es exclusivamente la interpolación posterior de sus datos para obtener una superficie continua, sí que es cierto que la interpolación se ha de basar en un muestreo previo, por lo que ambos conceptos van íntimamente unidos. Por ello, analizaremos en esta sección algunas de las ideas fundamentales que deben conocerse para diseñar un muestreo, y que directamente condicionan la calidad de la interpolación aplicada sobre el conjunto de puntos muestreados.

Lógicamente, el trabajar con una fracción reducida de la población introduce un cierto nivel de error. Ese error puede controlarse y acotarse mediante el diseño del muestreo. Por ello, a la hora de diseñar un muestreo deben plantearse principalmente las siguientes preguntas [ Haining2003Cambridge ]:

¿Qué se pretende estimar? Algunas propiedades no poseen componente espacial, y lo importante es el cuánto , no el dónde . Por ejemplo, la media de una variable. En el caso de la interpolación, sí es de gran importancia el dónde, puesto que, como ya sabemos, existe autocorrelación espacial y esta es utilizada como concepto inherente a los distintos métodos de interpolación.
¿Que tamaño de muestreo (número $n$ de muestras) se necesita para un nivel de precisión dado? El error está acotado en función de los puntos muestrales. En algunos casos se necesita realizar una estimación con un alto grado de precisión, y dentro de un amplio intervalo de confianza. En otros, sin embargo, no es necesario, y plantear un muestreo demasiado amplio supone un gasto innecesario de recursos.
¿Dónde tomar esas $n$ muestras? Por la existencia de autocorrelación espacial o por la variación espacial que pueden presentar otras variables relacionadas, una de las partes más importantes del muestreo es determinar la localización exacta en la que tomar las muestras. Existen tres modelos básicos de muestreo: aleatorio, estratificado y regular (Figura \ref{Fig:Tipos_muestreo})

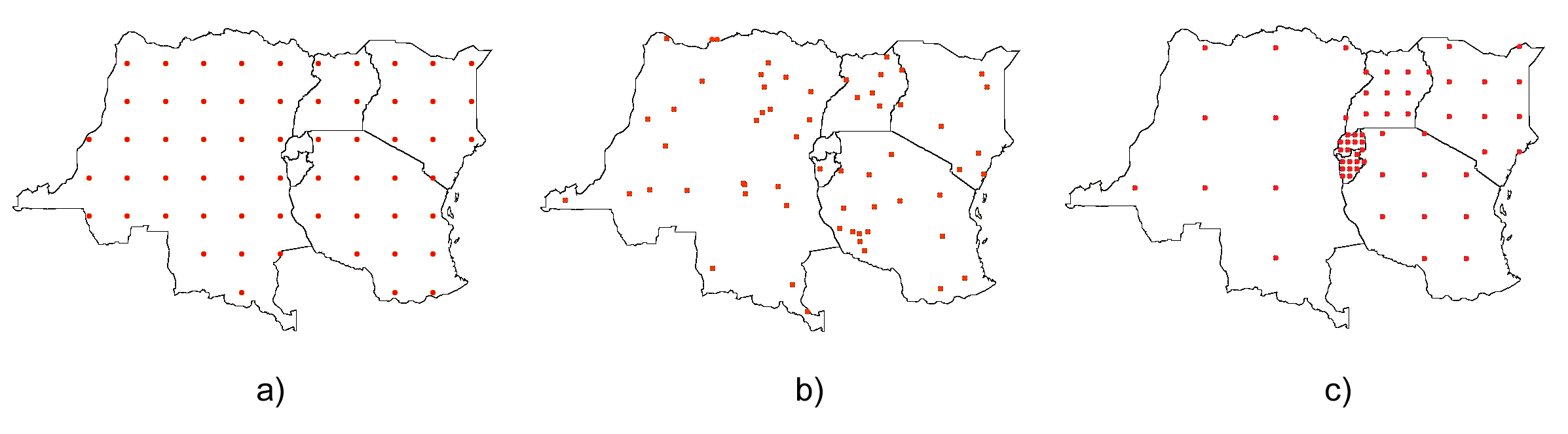
Tipos de muestreo. a) regular, b) aleatorio, c) estratificado
$$\label{Fig:Tipos_muestreo}$$

El muestreo aleatorio simplemente sitúa los puntos de muestreo al azar sin obedecer a ningún condición particular. Si se desconoce el comportamiento de la variable muestreada, un muestreo aleatorio puede ser una buena opción.

El muestreo regular sitúa puntos a intervalos fijos, constituyendo lo que se conoce como una malla de muestreo .

Por último, el muestreo estratificado requiere la presencia de una variable adicional relacionada. Si esta variable se encuentra zonificada, podemos subdividir el muestreo haciendo uso de las distintas zonas. Por ejemplo, si muestreamos una serie de parcelas donde estudiamos la altura media de sus árboles y disponemos de información sobre el tipo de suelo, podemos muestrear por separado para los distintas clases de suelo, ya que este tiene influencia sobre el crecimiento de los pies. Esto aumenta la precisión del muestreo, ya que en lugar de una única población heterogénea, se tienen un numero de subpoblaciones más homogéneas, en virtud de la agrupación según un factor común.

Los diseños pueden combinarse para obtener resultados más satisfactorios. Por ejemplo, puede hacerse un diseño estratificado y en cada uno de los estratos (cada zona definida por la variable adicional) plantear un muestreo regular con un tamaño particular de malla o incluso con un número de puntos a muestrear distinto en cada estrato.

Aplicando conjuntamente todo lo anterior debe tratar de diseñarse un muestreo que cumpla con lo siguiente:

Explicar la variabilidad de la variable lo mejor posible. Así, en el caso de plantear un muestreo que complemente a uno previo, ya se dispone de información acerca de la variable muestreada. Esta puede emplearse para distribuir adecuadamente los nuevos puntos de muestreo, aplicando que, por ejemplo, se necesitan más muestras en zonas de alta variabilidad.
El empleo de los denominados muestreos pilotos es una herramienta para conocer en primera aproximación las propiedades de la variable a estudiar y diseñar el muestreo acorde con estas.
Ser representativa. Esta representatividad debe ser tanto en el espacio de atributos como en el espacio geográfico, según puede verse en la figura \ref{Fig:Representatividad_muestreo}

El muestreo a) es representativo en el espacio de atributos pero no en el geográfico. El b), sin embargo, es representativo en el espacio geográfico pero no en el de atributos.

La figura muestra también algunas de las principales debilidades que pueden encontrarse en los distintos métodos de diseño de muestreo. Si la variable exhibe un comportamiento periódico, un muestreo regular puede enmascarar la existencia de dicha periodicidad y no ser representativo en el espacio de atributos. Ese es el caso del ejemplo a). En general, si existe algún tipo de orden oculto en la variable a analizar, debe tenerse cuidado a la hora de emplear muestreos sistemáticos, para evitar estos fenómenos. En el caso del ejemplo a), aunque no es un muestreo sistemático, la estructura de los puntos muestrales es bastante regular, lo que provoca que no se obtenga la representatividad en el espacio de atributos, dada la estructura periódica de la variable en el eje $x$.

En el ejemplo b) el muestreo no es representativo del espacio geográfico ya que el diseño deja grandes áreas sin ser muestreadas. Esto puede suceder al emplear muestreos aleatorios, ya que estos, por su propia aleatoriedad, pueden generar estructuras que dejen amplias zonas sin ser muestreadas o con una intensidad de muestreo insuficiente.

Elección del método adecuado

Junto a los métodos de interpolación que hemos visto, que son los más comunes y los implementados habitualmente, existen otros muchos que aparecen en determinados SIG tales como los de vecino natural [ Sibson1981Wiley ], interpolación picnofiláctica [ Tobler1979JASA ], u otros. Además de esto, cada uno de dichos métodos presenta a su vez diversas variantes, con lo cual el conjunto global de metodologías es realmente extenso. A partir de un juego de datos distribuidos irregularmente, la creación de una malla ráster regular es, pues, una tarea compleja que requiere para empezar la elección de un método concreto. Este proceso de elección no es en absoluto sencillo.

No existe un método universalmente establecido como más adecuado en todas situaciones, y la elección se ha de fundamentar en diversos factores. Al mismo tiempo, un método puede ofrecer resultados muy distintos en función de los parámetros de ajuste, con lo que no solo se ha de elegir el método adecuado, sino también la forma de usarlo. Entre los factores a tener en cuenta para llevar esto a cabo, merecen mencionarse los siguientes:

Las características de la variable a interpolar . En función del significado de la variable, las características de un método pueden ser adecuadas o no. Si, por ejemplo, interpolamos valores de precipitación máxima anual, no es adecuado utilizar aquellos métodos que suavicen excesivamente la superficie resultante, ya que se estarían perdiendo los valores extremos que, por la naturaleza del valor interpolado, son de gran interés.
Las características de la superficie a interpolar . Si conocemos a priori algunas características adicionales de la superficie resultante, algunos métodos permiten la incorporación de estas características. Por ejemplo, variaciones bruscas en puntos de discontinuidad tales como acantilados en el caso de interpolar elevaciones son aplicables mediante la imposición de barreras con métodos como el de distancia inversa, pero no con otros como el kriging.
La calidad de los datos de partida . Cuando los datos de partida son de gran precisión, los métodos exactos pueden tener más interés, de cara a preservar la información original. Si, por el contrario, sabemos que los datos de partida contienen mucho ruido, aquellos métodos que suavizan el resultado tales como el kriging son preferibles, de cara a atenuar el efecto de dicho ruido.
El rendimiento de los algoritmos . Algunos algoritmos como los basados en distancia son rápidos y requieren un tiempo de proceso aceptable incluso en conjuntos de datos de gran tamaño. Otros, como el kriging, son mucho más complejos y el tiempo de proceso es elevado. A esto hay que sumar la configuración propia del método, con lo que crear una capa ráster con algunos métodos puede llevar mucho más tiempo que con otros y requerir un esfuerzo mayor.
El conocimiento de los métodos . Por obvio que parezca, debe conocerse bien el significado del método para poder aplicarlo. Un método de gran complejidad como el kriging exige una sólida base de conceptos geoestadísticos para su aplicación. Más aún, el elevado número de ajustes que requiere y la alta sensibilidad del método a la variación de estos valores refuerza lo anterior.
La figura \ref{Fig:Kriging_resultados} muestra tres capas interpoladas mediante kriging a partir de un conjunto de puntos. El empleo de distintos ajustes y variogramas (lógicamente, no todos correctos) da lugar a capas muy diferentes. Si no se emplea correctamente, un método de interpolación puede producir resultados carentes de sentido, que aunque dan lugar a una capa con datos en todas sus celdas, dichos datos pueden no ser adecuados.

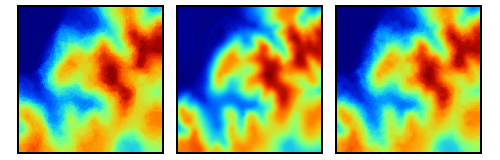
Distintos resutlados obtenidos por kriging a partir de un mismo juego de puntos, utilizando diferentes ajustes.
$$\label{Fig:Kriging_resultados}$$

Pese a lo anterior, el kriging es utilizado habitualmente sin considerar estos aspectos, obteniéndose resultados aparentemente correctos pero con frecuencia erróneos. La experiencia del usuario es un elemento clave en la aplicación de métodos de interpolación, y debe ponerse gran énfasis en este aspecto.

No debe olvidarse tampoco que algunos métodos asumen que se dan ciertas condiciones de los datos de partida, y esto puede no ser cierto, o bien requerirse algún tipo de transformación para que así suceda. Es necesario siempre comprobar que se dan estos supuestos.
El uso de la capa resultante . No es lo mismo utilizar un MDE para crear una vista 3D con una fotografía aérea, que emplearlo para crear una ortofoto. Los requerimientos de calidad en el primer caso son menores, tan solo de tipo visual, y cualquiera de los métodos puede sernos válido. Aplicar una metodología compleja y laboriosa quizás no sea la mejor opción en este caso, y sí lo sea el empleo de una más sencilla.

Elección de las características de la capa resultante

Los métodos que hemos visto en este capítulo no imponen restricciones sobre la distribución o el número puntos de entrada (si bien el kriging, por ejemplo, exige un cierto número de puntos para un ajuste fiable del variograma teórico), ni tampoco sobre las características de la capa ráster resultante. A pesar de ello, resulta claro que existe una relación directa entre ambas, y que la capacidad de un conjunto de valores puntuales para generar una capa ráster es limitada.

En la práctica, a partir de cualquier capa de puntos podemos obtener cualquier capa ráster, ya que pueden siempre calcularse los valores en las celdas. Pero si aplicamos algunos conceptos cartográficos e ideas básicas de teoría de la información, no es difícil darse cuenta de que esto puede ser incorrecto. Existen unas características idóneas para la capa ráster interpolada, fuera de las cuales no es adecuado interpolar.

Vimos en Modelo_raster que la resolución horizontal o tamaño de celda era uno de los parámetros básicos que definían las características de una capa ráster. Existiendo relación entre los puntos de origen y la capa interpolada a partir de ellos, debe existir por igual una relación entre la distribución espacial de los valores puntuales y dicho tamaño de celda, pues ambos elementos definen la precisión con que se recoge la variable estudiada.

Cuando el número de puntos no es suficiente para ello, crear una capa con una resolución alta (tamaño de celda pequeño) equivale a generar un resultado cartográficamente incorrecto. Por el contrario, interpolar con un tamaño de celda demasiado grande supone estar desperdiciando parte de la información de partida, lo cual, en el caso de trabajar sobre un muestreo realizado específicamente para ello, implica un malgasto de medios materiales y humanos en la recogida de datos. La elección del tamaño de celda adecuado es, por tanto, fundamental en el proceso de interpolación.

Los conceptos que vamos a ver a este respecto pueden emplearse tanto para estimar el tamaño de celda de la capa a interpolar, como para ayudar en el diseño del muestreo previo a la creación de esta. Así, si conocemos de antemano (por ejemplo, por el uso que le vamos a dar) las características de la capa que necesitamos generar, podemos diseñar de forma más correcta el muestreo haciendo uso de estas ideas.

[ Hengl2006CG ] argumenta que el tamaño de celda adecuado de una capa ráster es función de la escala, la capacidad de proceso, la precisión posicional, la densidad de muestreo, la correlación espacial existente y la complejidad de la superficie a interpolar. Según estos conceptos, define tamaños mínimos y máximos de celda para cada circunstancia y cada factor considerado de los anteriores. Asimismo, recomienda una solución de compromiso entre los citados valores extremos.

Para la densidad de muestreo, se considera que, por ejemplo para la toma de datos de suelo, por cada centímetro cuadrado del mapa debe existir al menos una muestra [ Avery1987Soil ]. Aplicando los conceptos que vimos en Escala , se llega a una resolución óptima

\begin{equation} \Delta s = 0.0791 \sqrt{\frac{A}{N}} \end{equation} siendo $A$ el área de la zona a interpolar y $N$ el número de puntos disponibles.

Si, en lugar de lo anterior, aplicamos criterios basados en la disposición geométrica de los puntos, se llega a un valor

\begin{equation} \Delta s = 0.5 \sqrt{\frac{A}{N}} \end{equation}

La gran diferencia existente entre este tamaño recomendado y el anterior se debe al hecho de que este último es válido únicamente para patrones de puntos completamente regulares. En el caso de patrones aleatorios o agregados se deben aplicar consideraciones distintas. Por ejemplo, para el caso de un patrón agregado, la distancia media entre puntos es aproximadamente la mitad de la existente en un patrón regular con el mismo número de puntos. Por ello, la anterior fórmula quedaría como

\begin{equation} \Delta s = 0.25 \sqrt{\frac{A}{N}} \end{equation}

Aunque resulta imposible dar una cifra exacta para la resolución óptima considerando todos los factores implicados, valores recomendados como los anteriores son de gran utilidad para poder al menos tener una idea del intervalo en el que el tamaño de celda a escoger debe encontrarse. Sin constituir «recetas» infalibles a la hora de elegir un tamaño de celda, constituyen herramientas útiles que deben considerarse antes de interpolar un conjunto de puntos.

Comprobación del ajuste. Validación

Algunos métodos como el kriging dan una estimación del error además de la capa de valores interpolados. En los métodos aproximados tales como el ajuste de funciones polinómicas, puede calcularse el residuo cuadrático según

\begin{equation} \varepsilon = (\widehat{z} - z)^2 \end{equation}

Es decir, como el cuadrado de la diferencia entre el valor real y el estimado.

En los métodos exactos, por propia definición, este valor es cero, lo cual no quiere decir, lógicamente, que la capa interpolada sea «perfecta» (lo es, pero solo en los puntos de partida), ni que no pueda llevarse a cabo una validación.

Una forma habitual de proceder es, si se dispone de un juego grande de datos (con muchos puntos), «reservar» algunos de ellos para una validación posterior. Se interpola así una capa a partir de la mayor parte de ese conjunto, y se comprueba la diferencia entre los valores estimados en los puntos restantes y los valores medidos en dichos puntos. Los valores estimados en esos puntos no han sido influenciados por los valores reales, ya que no estos se han empleado en la interpolación.

Si no disponemos de un conjunto de datos de validación y el juego de datos disponible es reducido y no podemos separar una parte de él para validar el resultado, podemos llevar a cabo un proceso de validación cruzada. En este proceso, se calculan por interpolación puntos en cada una de las coordenadas de los puntos de muestreo, empleando en cada caso todos los puntos restantes.

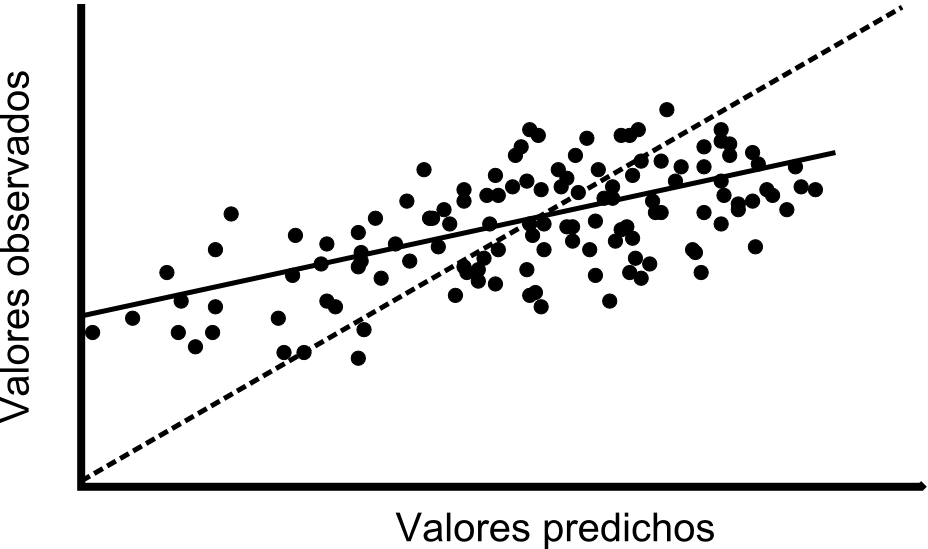
De esta forma, obtenemos un conjunto de pares de valores con los valores reales y estimados en cada punto, que podemos mostrar en una gráfica como la de la figura \ref{Fig:Validacion_cruzada}. De igual modo, podemos efectuar un análisis de regresión y obtener la expresión de la recta de ajuste, el coeficiente de correlación de esta o el residuo medio cuadrático. El valor representativo en este caso, no obstante, es la propia expresión de la función. En caso de un ajuste perfecto, la recta debe ser de la forma $y=x$, por lo que resulta interesante representar esta recta ideal para poder comparar.

Validación cruzada previa de datos puntuales para interpolación.

Densidad

Además de los métodos de interpolación, hay otro tipo de operaciones que pueden realizarse sobre capas de puntos, y que dan como resultado capas ráster.

Supongamos el siguiente caso. Se tiene una capa de puntos como la de la figura \ref{Fig:Densidad} que indica los registros de observación de una determinada especie. Si queremos crear un mapa de densidad de individuos, nos encontramos en un caso similar al que implica la interpolación: la carencia de datos a lo largo de todo el espacio. En este caso, al igual que entonces, podemos aplicar formulaciones específicas para calcular dicha densidad.

Como se vio en el apartado Analisis_patrones_puntos , la densidad representa la intensidad (propiedad de primer orden) del patrón de puntos, que es una realización concreta del proceso de puntos que lo ha generado.

Por simplicidad, ignoraremos por el momento los atributos asociados a cada punto. Es decir, consideraremos únicamente el dato espacial, que nos dice que en las coordenadas del punto ha sido observada una especie. Asociando a cada punto un área de influencia (por ejemplo, el radio de movimiento conocido de la especie), podemos calcular la capa de densidad de esta sin más que contar en cada celda el número de puntos observados cuyo área de influencia incluye a dicha celda, y dividiendo después por la superficie del área de influencia.

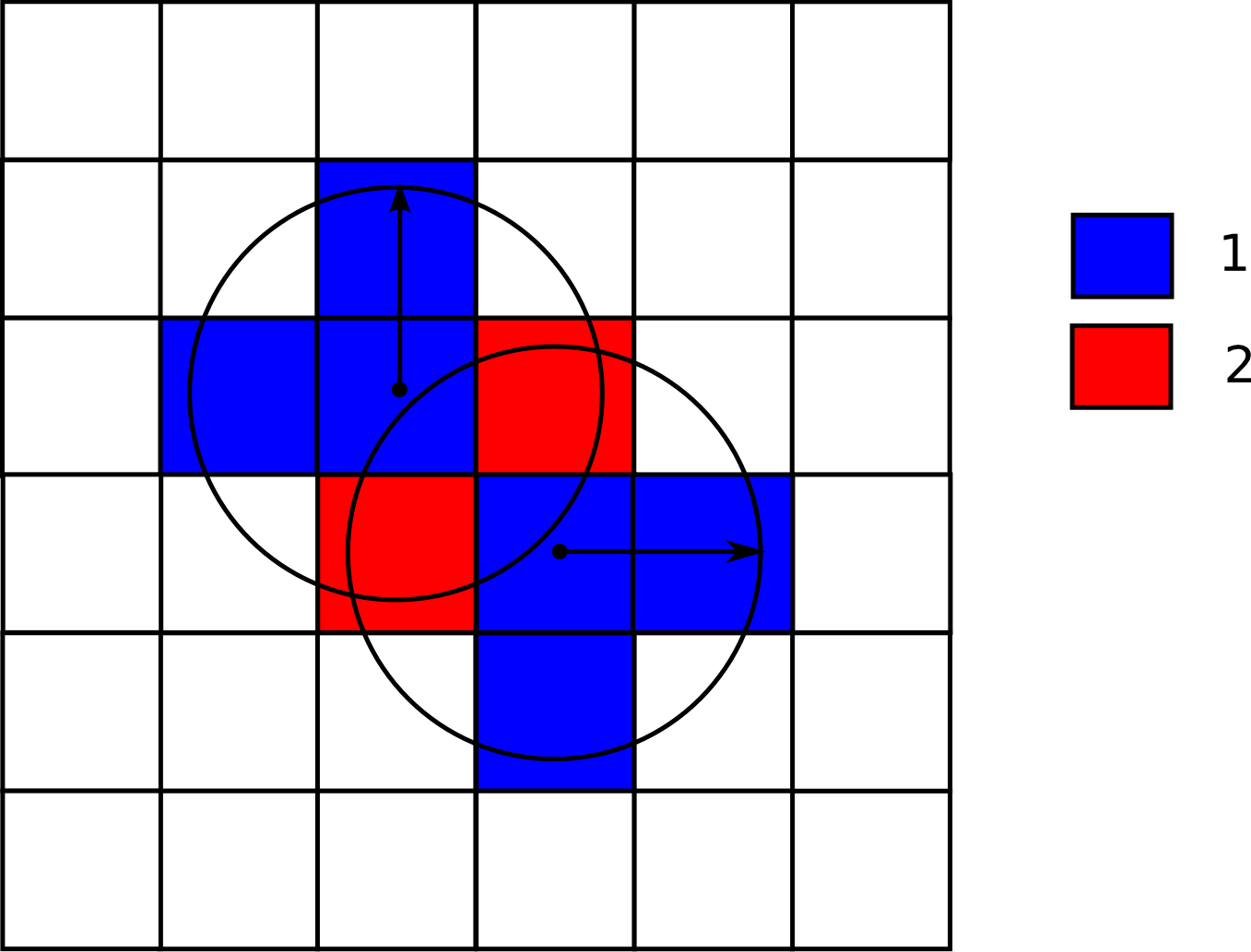
La figura \ref{Fig:Densidad_sencillo} muestra un ejemplo sencillo con la áreas de influencia de dos únicos puntos. Donde ambas áreas intersecan, la densidad es, lógicamente, mayor. Las celdas que no están en el área de influencia de ningún punto tienen un valor de densidad nulo.

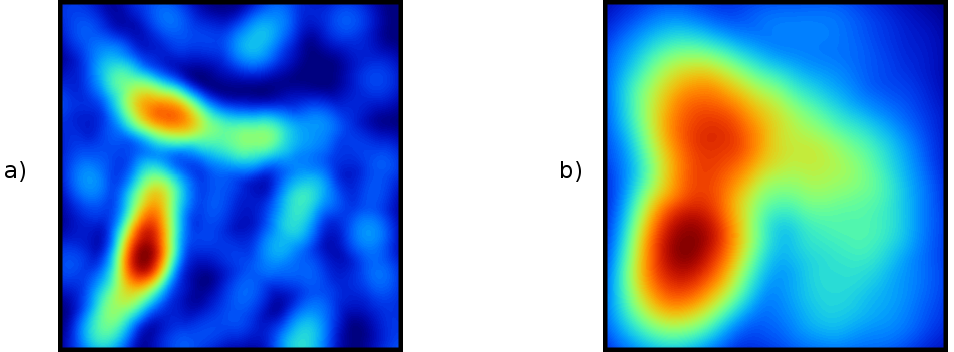
Esquema del cálculo de densidades utilizando un área de influencia fija.

$$\label{Fig:Densidad_sencillo}$$

La elección del área de influencia afecta directamente al resultado obtenido, tal como puede verse en la figura \ref{Fig:Densidad}, que muestra dos capas de densidad calculadas para distintos radios de influencia.

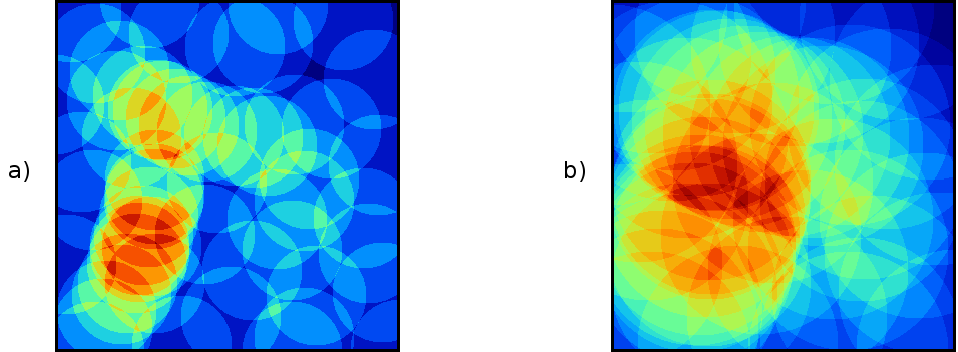
Capas de densidad a partir de una capa de puntos. El tamaño del radio de influencia en (b) es el doble que en (a).

Se asume por defecto que el área de influencia es circular (mismo alcance de dicha influencia en todas direcciones), y que es la misma para todos los puntos.

En realidad, puede entenderse la creación de una capa de densidades como un histograma bidimensional, siendo por tanto una función de probabilidad.

La pertenencia o no al área de influencia de cada punto es una función discontinua. Para crear capas de densidad con transiciones suaves, pueden utilizarse funciones distintas, de modo que la influencia varíe con la distancia de forma continua.

En estadística, una función núcleo o núcleo (kernel) es una función de densidad bivariante y simétrica, empleada en la estimación de funciones de densidad de probabilidad de variables aleatorias. El caso anterior en el que todos puntos de la ventana de influencia tienen el mismo peso es un caso particular de núcleo, pero existen muchos otros que dan lugar a estimaciones no discontinuas.

La teoría acerca de este tipo de funciones y su uso no se desarrollará aquí, pudiendo consultarse, por ejemplo, en [ Silverman1986Chapman ].

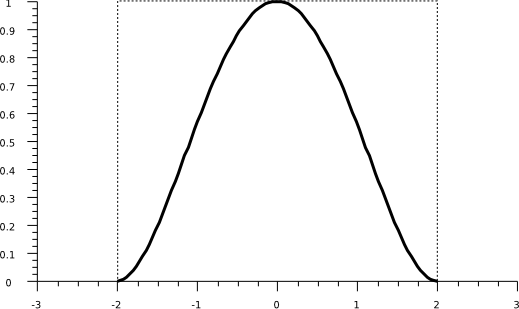
Un núcleo de uso frecuente es el mostrado en la figura \ref{Fig:Nucleo_gaussiano}, denominado gaussiano , cuya aplicación resulta en capas suavizadas y continuas (Figura \ref{Fig:Densidad_kernel}), y cuya expresión es

\begin{equation} k(h)=\left(1-\frac{h^2}{r^2}\right)^2 \qquad \forall h \leq r \end{equation}

donde $h$ es la distancia al punto y $r$ el radio máximo de influencia.

Comparación entre una función núcleo constante (en trazo punteado) y un núcleo gaussiano (en trazo continuo) para un radio de influencia $r=2$.

Como puede observarse comparando las figuras \ref{Fig:Densidad} y \ref{Fig:Densidad_kernel}, la diferencia entre el uso de uno u otro núcleo es notable, pero la utilización de radios distintos, independientemente del método empleado, da lugar a resultados muy diferenciados. El radio de influencia máxima es, pues, el parámetro más importante en la estimación de densidades, y debe seleccionarse de acuerdo con la distribución de los puntos muestrales.

Capas de densidad a partir de una capa de puntos mediante nucleo gaussiano. El tamaño del radio de influencia en (b) es el doble que en (a).

Además de emplear las coordenadas de cada punto para la estimación de densidad, pueden ponderarse estos con los atributos de cada uno de ellos. Así, partiendo de una capa de puntos que represente núcleos poblacionales, para cada uno de los cuales se disponga de su número de habitantes, puede obtenerse una capa de densidad de población. O, en el caso de los puntos que representan observaciones de individuos de una especie, recoger en estos puntos no solo el hecho de que se ha producido un avistamiento, sino cuántos de ellos.

La figura \ref{Fig:Densidad_sencillo_ponderada} muestra un ejemplo del cálculo de densidades si se emplea ponderación de los puntos.

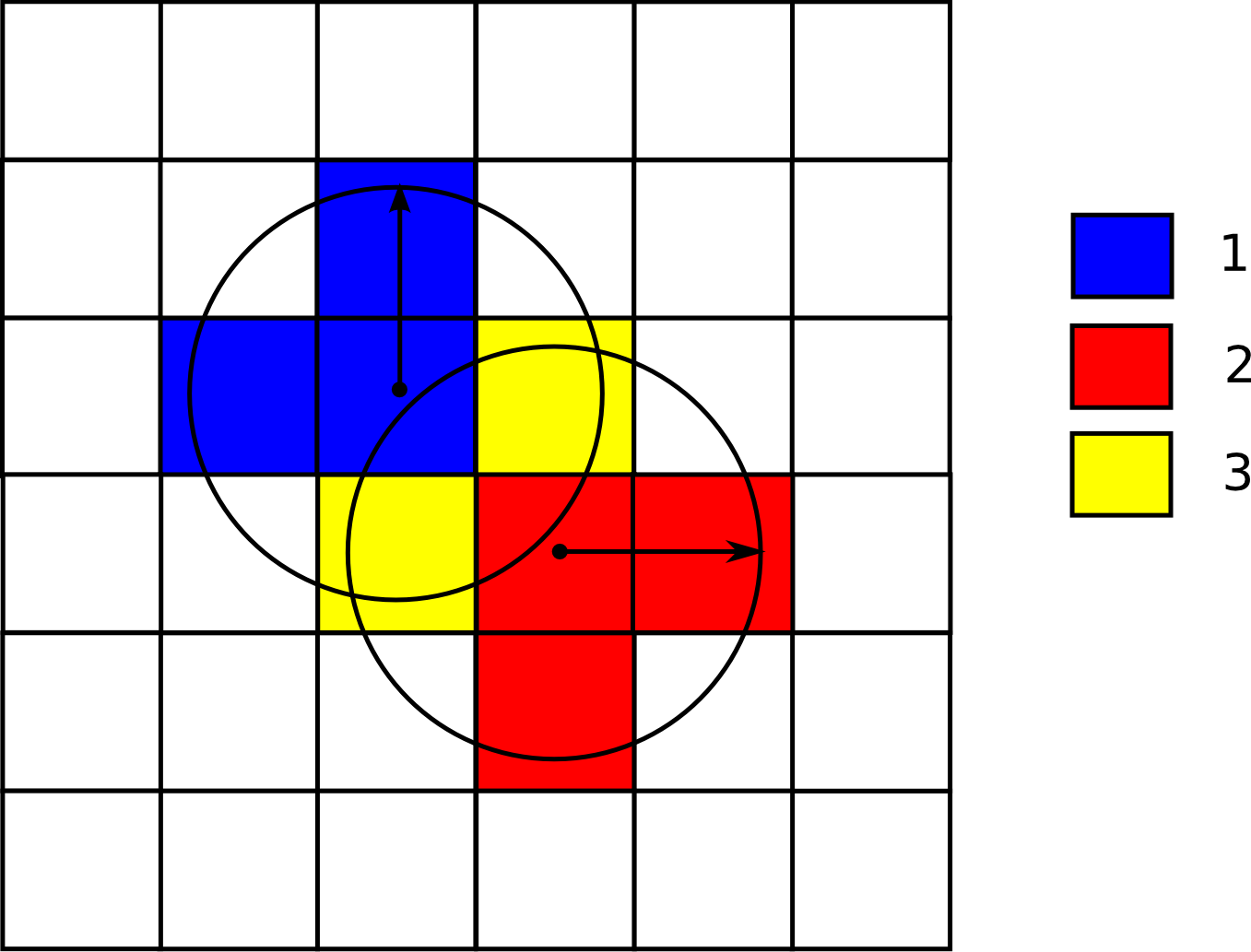
Esquema del cálculo de densidades utilizando un área de influencia fija y ponderación según valores. El punto inferior derecho tiene un peso $p=2$, mientras que el superior izquierdo un peso $p=1$.

En el caso de las observaciones de una especie, la capa de densidad nos da igualmente una medida de la probabilidad de encontrar esa especie en cada celda. El cálculo de estas probabilidades es la base para el desarrollo de modelos predictivos más complejos. Estos modelos incluyen la utilización de variables de apoyo, así como muestreos no solo de presencia, sino también de ausencia.

Resumen

La información vectorial, en particular la disponible en forma de puntos, puede convertirse en capas ráster a través del uso de métodos de interpolación. Estos permiten calcular valores en puntos no muestreados, a partir de valores recogidos en una serie de localizaciones. De este modo, se puede asignar un valor a cada celda de una capa ráster, y crear una representación continua de la variable recogida en los puntos de muestreo.

Existen muchos métodos de interpolación distintos, entre los que cabe destacar los siguientes por su implementación habitual en los SIG:

Vecino más cercano
Ponderación por distancia
Ajuste de polinomios
Curvas adaptativas
Kriging

La elección del método a emplear debe realizarse en función del tipo de datos a interpolar, las características de estos, y los requerimientos y usos previstos de la capa resultante, entre otros factores. Asimismo, es importante elegir una resolución de celda adecuada y, en caso que los puntos de muestreo no vengan dados a priori , diseñar un muestreo óptimo.

Empleando métodos de validación y validación cruzada, puede comprobarse la bondad de ajuste de la capa interpolada y la validez de los datos de partida y el modelo empleado.

Junto con los métodos de interpolación, el calculo de densidades permite igualmente la creación de capas ráster a partir de datos puntuales.