Álgebra de mapas

Introducción

Se entiende por álgebra de mapas el conjunto de técnicas y procedimientos que, operando sobre una o varias capas en formato ráster, nos permite obtener información derivada, generalmente en forma de nuevas capas de datos. Aunque nada impide que este proceso se lleve a cabo sobre capas vectoriales, se entiende que el álgebra de mapas hace referencia al análisis desarrollado sobre capas ráster, pues estas, por su estructura regular y sus características inherentes, son mucho más adecuadas para plantear los algoritmos y formulaciones correspondientes. Los procedimientos que se aplican sobre información geográfica vectorial se clasifican generalmente dentro de otros bloques de conocimiento, como es por ejemplo el caso de las operaciones geométricas (incluidas dentro de la geometría computacional), cuyos procesos se tratarán en el capítulo Operaciones_geometricas .

Conviene aclarar que, en la práctica y el uso diario de los SIG, el término álgebra de mapas suele utilizarse de forma errónea. Ello es debido a que la gran mayoría de las aplicaciones SIG implementan algún tipo de funcionalidad para la combinación de un número dado de capas ráster, de forma que pueden relacionarse mediante expresiones matemáticas para la obtención de una nueva capa, y esta funcionalidad se designa normalmente como álgebra de mapas o en ocasiones calculadora de mapas .

La gran utilidad de esta funcionalidad y su uso habitual hacen que se asocie casi exclusivamente con ella el concepto de álgebra de mapas, olvidando —o desconociendo—, que también las restantes funcionalidades de análisis emplean el álgebra de mapas como base fundamental. Es por ello más correcto utilizar en tal caso esa segunda denominación, calculadora de mapas , para dichas herramientas, ya que, si bien el uso de estas operaciones entre capas es una aplicación de los conceptos propios del álgebra de mapas, no es la única, y no debe pensarse que todo él es expresable de ese modo.

Como tal, el álgebra de mapas lo forman un conjunto de variables (los mapas), expresiones y funciones, los cuales, a través de una sintaxis adecuada, permiten la obtención de nuevos resultados geográficos. Las funciones que se implementan en las calculadoras de mapas son, como veremos, un subconjunto de las posibles, lo que bien podríamos denominar una aritmética de mapas . El concepto de álgebra de mapas, más extenso que el anterior, constituye sin embargo no una herramienta puntual, sino un completo marco de trabajo para el manejo de capas ráster y, muy especialmente, su análisis encaminado a la obtención de nuevos resultados.

Si analizamos las practicas geográficas hasta nuestros días, vemos que el álgebra de mapas como proceso de análisis no es algo nuevo. La idea de utilizar mapas existentes para generar otros nuevos o simplemente extraer de ellos resultados cuantitativos es una práctica común desde el mismo momento en que aparece la cartografía moderna. Sin embargo, es con la aparición de los Sistemas de Información Geográfica y la posibilidad de procesar los datos geográficos en un entorno informatizado cuando se dota de formalismo a estos planteamientos y se define con rigor el conjunto de herramientas de análisis.

La definición actual del álgebra de mapas la debemos a Dana Tomlin [ Tomlin1990Prentice ], quien estableció la división principal de funciones y dio cuerpo a la disciplina, sentando así las bases para lo que es hoy en día la manera habitual de proceder en el análisis de capas geográficas ráster. Posteriormente, otros autores han desarrollado generalizaciones y extensiones de las ideas de Tomlin, pero son estas las que, desde el punto de vista práctico, cubren la mayor parte de casos posibles y resultan de utilidad directa para el análisis habitual.

Más allá de lo que se desarrolla en este capítulo, las ideas que veremos a continuación se van a repetir de forma continua en la mayoría de capítulos de esta parte, pues constituyen la base formal y conceptual de los análisis que siguen en dichos capítulos.

Para comenzar el estudio del álgebra de mapas, veamos unos casos prácticos que nos servirán para introducir con posterioridad los elementos básicos. En primer lugar, consideremos la siguiente expresión, que define la bien conocida Ecuación Universal de Pérdidas de Suelo (USLE) [ Wischmeier78USDA ]

\begin{equation} \label{Eq:USLE} A = R\cdot K \cdot LS \cdot C \cdot P \end{equation}

donde $A$ representa las pérdidas totales en toneladas por hectárea y año, y los factores $R, K, LS, C$ y $P$ representan la influencia de los diversos factores (agresividad del clima, tipo de suelo, topografía, uso de suelo, y prácticas de conservación) sobre dichas pérdidas. La USLE representa, por tanto, un modelo sencillo que combina cinco variables, todas ellas susceptibles de ser recogidas en las correspondientes capas ráster. Si extendemos el cálculo puntual de la variable $A$ a todos los puntos de la zona estudiada, obtendremos una nueva capa de dicha variable, evaluando la anterior expresión para cada una de las celdas de esas capas ráster (Figura \ref{Fig:USLE}).

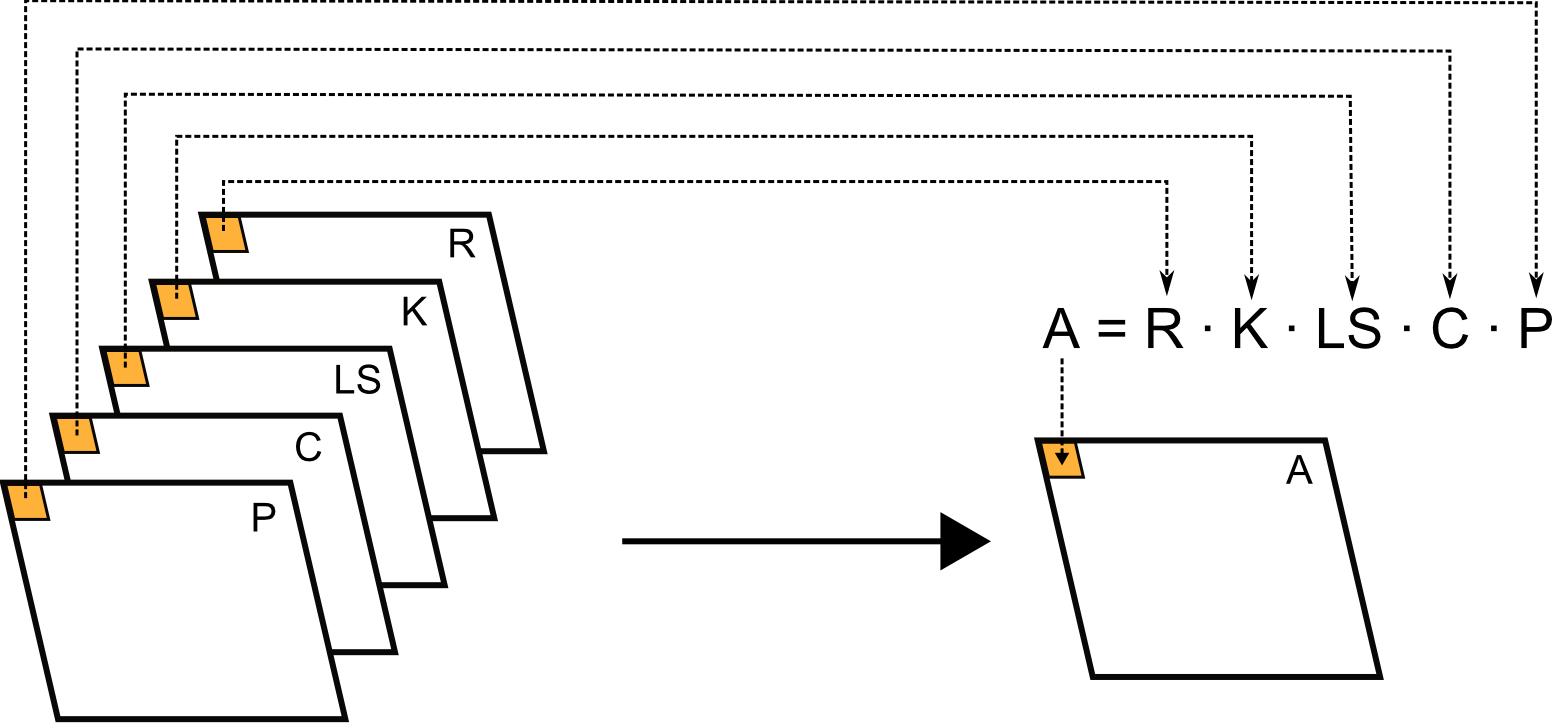
Puede extenderse una formula algebraica tal como la de la Ecuación Universal de Pérdidas de Suelo (USLE) a un conjunto de capas. Basta operar celda a celda con las capas que contienen las variables implicadas, para obtener una nueva capa resultante con el conjunto de valores calculados.

La discretización del espacio que implica la representación en formato ráster de un parámetro sobre una superficie dada, hace que ese análisis de «todos los puntos» se materialice en un análisis de todas las celdas que contiene la nueva capa a obtener. Esto nos hace ver la idoneidad de este formato para trasladar las ideas matemáticas de modelos sencillos como la USLE a un álgebra de mapas donde estos modelos no se apliquen en un emplazamiento concreto, sino en toda una región de interés a tratar.

En este caso, basta con aplicar la expresión mostrada en la figura \ref{Fig:USLE} celda a celda, y obtener tantos valores resultantes como celdas haya, que conformarán una nueva capa con la distribución espacial de las pérdidas de suelo correspondientes.

Consideremos ahora que, junto con el mapa de pérdidas de suelo obtenido según lo anterior, disponemos de una división en subcuencas de la zona de estudio. Puede resultar interesante asociar a cada una de las unidades hidrológicas un valor relacionado con los valores de pérdidas de suelo que se dan en ella. Por ejemplo, la media de los valores de pérdidas de suelo de todas las celdas de la subcuenca. Partiendo de estos dos mapas, podemos obtener un tercero que nos indique las pérdidas medias en cada cuenca, de interés sin duda para localizar las unidades que puedan presentar mayores problemas de erosión (Figura \ref{Fig:USLE_por_subcuencas}).

Valores de pérdidas de suelo por subcuencas.

La base conceptual en este caso vemos que es distinta al primer supuesto, ya que no extendemos ningún modelo puntual aplicándolo en todas las celdas con distintos valores de entrada para cada una de ellas, sino que estas van a contener un valor medio asociado al total de celdas incluidas en su misma subcuenca. Esta forma de proceder ya no se corresponde con el caso anterior y no puede ser llevada a cabo con las funcionalidades de calculadora de mapas que citábamos como habituales en los SIG, ya que no se da un análisis entre capas celda a celda, sino un análisis dentro de la propia capa con otras celdas relacionadas a través de esa pertenencia a la misma unidad hidrológica. No obstante, como veremos, este tipo de funciones también forman parte del álgebra de mapas.

Por último, supongamos que es de interés estudiar la distribución de valores de esas pérdidas de suelo. Un histograma de frecuencias resultaría de gran utilidad. En este caso, el análisis trabaja una vez más sobre la capa de pérdidas de suelo, pero no genera nuevos resultados geográficos. Aun así, la generación de nuevas capas no es una condición básica del álgebra de mapas, ya que sus procesos pueden tener como resultado elementos muy diversos.

Todos estos ejemplos son parte de los resultados que pueden obtenerse utilizando los distintos componentes del álgebra de mapas, que a continuación detallaremos.

Tipos de funciones en el álgebra de mapas

Las funciones son el elemento principal del álgebra de mapas. Cuatro son los tipos principales de funciones que podemos definir, agrupadas según la forma en que toman la información necesaria para su cálculo de entre la contenida en todas las celdas de las capas de origen.

Local . El valor en cada celda de la capa resultante es función únicamente de los valores en esa misma celda en las capas de partida.
Focal . El valor en cada celda de la capa resultante es función del valor en dicha celda y en las situadas en un entorno definido alrededor de la misma.
Zonal o regional . El valor en cada celda de la capa resultante es función del valor de todas las celdas conectadas a esta que presentan un mismo valor para una de las capas de entrada (pertenecen a la misma clase que esta).
Global . El valor resultante de la función es obtenido a partir de todas las celdas de la capa.

La combinación de distintas funciones y de enfoques variados da lugar a un enorme conjunto de operaciones de análisis basadas en el álgebra de mapas así definido. Este conjunto es el que dota de toda su potencia a los SIG como herramientas de análisis del medio, y permite extraer de los datos geográficos en formato ráster toda la información que realmente contienen.

Funciones locales

Las funciones de análisis local analizan los valores de una celda concreta en una serie de capas para obtener el valor resultante. En rojo, celdas de partida analizadas. En verde, celda que recoge el resultado.

Las funciones locales asignan valores a una celda en base a los valores que esa misma celda presenta para cada una de las capas de entrada, operando con estos de una forma u otra. Es decir, el valor resultante para una localización dada es función exclusivamente de lo que se encuentra en dicha localización, no dependiendo en modo alguno de otras localizaciones (otras celdas) (Figura \ref{Fig:Funciones_locales}).

Las funciones locales son las que utilizamos cuando empleamos esa anteriormente citada aritmética de mapas , tal y como veíamos por ejemplo en el caso de la USLE. Aunque otro tipo de funciones también operan con varias capas, la combinación de una serie de ellas suele llevarse a cabo con funciones locales, que calculan los valores para cada punto de acuerdo con los valores de dichas capas en ese punto. El ejemplo de la USLE es una función sumamente sencilla, que tan solo multiplica las capas de partida, pero pueden elaborarse funciones más complejas utilizando todos los operadores disponibles, que estudiaremos más adelante.

Una función de tipo local puede ser también aplicada sin necesidad de tener una serie de capas, sino con una única capa de partida. Por ejemplo, un cambio de unidades es una función local, ya que cada uno de los valores expresados en las unidades de destino solo depende del valor expresado en las unidades de origen en cada propia celda. Si una capa conteniendo elevaciones expresadas en metros la multiplicamos por 100, obtenemos una nueva capa con valores de elevación en centímetros, habiendo aplicado una función local para realizar la conversión.

De igual modo, convertir los valores de una capa de pendientes de radianes a grados requiere multiplicar sus valores por $180/\pi$.

Además de operar con escalares, podemos aplicar también funciones matemáticas. Por ejemplo, las capas que presentan un gran coeficiente de variación (elevada varianza en relación a la media de los valores de la capa) muestran mucha más información si aplicamos una transformación logarítmica. En la figura \ref{Fig:Transformacion_logaritmica} vemos una capa de área acumulada $a$ (este concepto hidrológico se explicará en el apartado Area_acumulada ) junto a otra que representa el parámetro $\log(a)$, apreciándose claramente la diferencia entre ambas en cuanto a la riqueza de información visual que aportan. Esta transformación logarítmica es una función local dentro del álgebra de mapas.

La aplicación de una transformación logarítmica modifica la representación visual de una capa. a) Capa original, b) capa tras trasformación logarítmica.

Una aplicación común de una función local con una sola capa la encontramos en la normalización de valores. En ocasiones, antes de efectuar un proceso que englobe a varias capas (por ejemplo, otra función de análisis local pero multicapa), es necesario homogeneizar estas de modo que todas se hallen en un mismo rango de valores. Este proceso se denomina normalización . Es habitual que el rango común sea el intervalo $(0,1)$, para lo cual se aplica a cada capa la función local definida por la siguiente expresión:

\begin{equation} y_{ij} = \frac{x_{ij} - x_{min}}{x_{max} - x_{min}} \end{equation}

donde $y_{ij}$ es el valor normalizado en la celda $ij$, $x$ el valor de esa celda en la capa inicial y $x_{min}$ y $x_{max}$, respectivamente, los valores mínimo y máximo de la variable en el conjunto de celdas de la capa.

Si en vez de aplicar una función matemática sobre el valor de cada celda, aplicamos una serie de criterios referidos a dicho valor mediante operadores de comparación, podemos llevar a cabo un proceso de clasificación. De este modo, podemos obtener a partir de una capa continua una capa discreta en la que las celdas serán clasificadas en grupos según el valor de la variable de partida, o bien reconvertir una clasificación ya existente en otra de acuerdo a unas condiciones establecidas. La figura \ref{Fig:Clases_pdte} muestra una clasificación de los valores de pendiente en clases, práctica habitual en muchas disciplinas a la hora de trabajar con este parámetro. Para ello se ha utilizado el siguiente criterio.

\begin{equation} s' = \left\{ \begin{array}{ll} 1 & \textrm{si } s \leq 5 \\ 2 & \textrm{si } 5\lt s \leq 10 \\ 3 & \textrm{si } 10 \lt s \leq 20 \\ 4 & \textrm{si } s\gt20 \end{array} \right. \end{equation}

donde $s'$ es la clase de pendiente, y $s$ el valor de la pendiente en porcentaje.

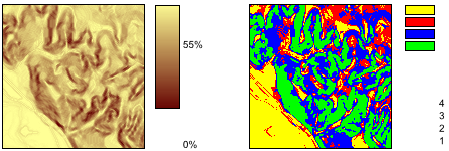
Mediante una función local de reclasificación, podemos convertir una capa de valores continuos en una capa de clases con información discreta.

También es posible reclasificar capas que ya contienen información categórica, sustituyendo los valores de una clase por un nuevo valor. Puede utilizarse para crear clasificaciones menos detalladas, agrupando clases similares en una única.

Dentro de las funciones locales sobre una única capa, podemos considerar como un caso particular la generación de nuevas capas «desde cero», es decir, sin basarnos en los valores de ninguna capa previa. Por ejemplo, crear una capa de valor constante $k$ o una capa con valores aleatorios dentro de un intervalo definido. En este supuesto, se toma de la capa origen solo su extensión y tamaño de celda, pero los valores son generados sin basarse en los existentes en ella.

Cuando las funciones locales se aplican a varias capas, la forma de combinar estas es muy variable. Junto a las operaciones que ya hemos visto, podemos utilizar algunas otras, y de modos igualmente variados. El conjunto de ellas lo dividimos en los siguientes grupos:

Operadores aritméticos . Para formar expresiones con las distintas capas tales como la ecuación USLE que ya conocemos.
Operadores lógicos . Pueden tomarse los valores de las capas como valores booleanos (1 o 0, verdadero o falso), o aplicar expresiones lógicas de tipo pertenece al conjunto u operadores de comparación, entre otros.
Parámetros estadísticos . Por ejemplo, el valor mayor de entre las todas las capas. También pueden recogerse otros como el orden del valor de una capa dentro de la serie ordenada de valores en todas las capas, el código de la capa donde aparece ese valor mayor, o el numero de capas con valores iguales a uno dado. La figura \ref{Fig:Analisis_local_estadistico} muestra algunos ejemplos simples basados en estas ideas.

Algunos ejemplos sencillos de análisis local estadístico con múltiples capas. En la fila superior, capas de origen y su numeración correspondiente. En la inferior, de izquierda a derecha: valor más frecuente (mayoría), valor máximo, y capa de máximo valor. ND indica celdas sin datos en las cuales no puede establecerse un valor resultante por no estar este bien definido.

Comenzando por el supuesto más sencillo de utilizar únicamente dos capas, podemos aplicar operadores lógicos tales como $, \neq, =, \leq$ o $\geq$. Por ejemplo, con dos capas con información categórica de usos de suelo correspondientes a dos fechas distintas, el operador de desigualdad nos servirá para detectar en la nueva capa resultante aquellas celdas donde el uso de suelo haya cambiado.

Cuando tenemos un conjunto mayor de capas, podemos aplicar los operadores anteriores, e incluso combinar operadores de varios grupos distintos de entre los anteriores. Por ejemplo, la técnica conocida como Ordered Weighted Average (OWA) [ Yager1988IEEESMC ], aplica una media ponderada de las capas de la forma

\begin{equation} y=\sum_{i=1}^n z_i k_i \ ; \ k_i \in \mathbb{N} \end{equation}

siendo $n$ el número de capas y $z_i$ el valor i--esimo de los de las distintas capas, ordenados estos en orden ascendente. El valor $i_1$ sería el más pequeño de todas las capas en la celda problema, y $i_n$ el mayor. Esto hace que el valor $z_i$ que se multiplica por $k_i$ no esté siempre asociado a una capa fija ($i$ no representa a una capa), sino a una posición dentro de la lista ordenada formada por los valores de todas las capas para cada celda.

La aplicación del OWA puede verse como un uso combinado de una función de análisis local de tipo estadístico que se encarga de generar nuevas capas con los valores i-esimos, y la posterior aplicación de una operación aritmética. Esta última ya se aplicaría de la forma habitual, pero sobre las capas provenientes de la primera operación, no sobre las originales.

Aunque si trabajamos con capas de tipo categórico carece de sentido desde un punto de vista conceptual el operar aritméticamente con valores que identifican una clase, las operaciones aritméticas nos pueden servir de igual modo en este caso para obtener nuevas capas. Una función local aritmética nos sirve como herramienta para realizar algunas tareas, entre ellas una habitual como es combinar en una sola capa dos clasificaciones distintas.

Partiendo de una capa de usos de suelo y una de tipos de suelo, podemos obtener una nueva clasificación que combine ambas (Figura \ref{Fig:Combinacion_capas_categoricas}). Un proceso como se realiza, por ejemplo, para el cálculo del Número de Curva [ USDA1986TR55 ], una variable hidrológica que permite calcular la generación de escorrentía a partir de una precipitación dada. La clase de Número de Curva se asigna en función del uso y el tipo de suelo. El proceso es, en realidad, una intersección de las zonas definidas por cada capa.

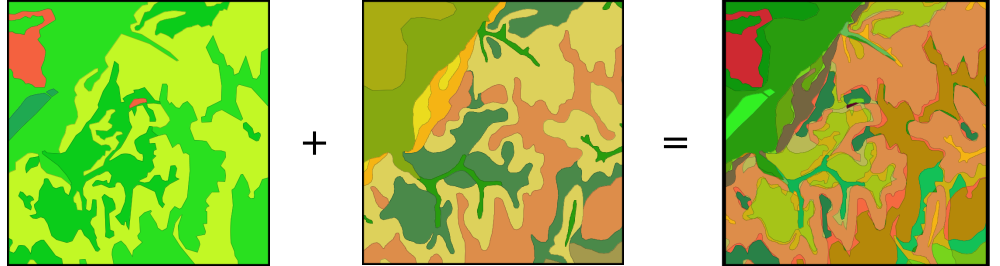
Combinación de dos capas categóricas para crear una nueva clasificación que une ambas.

Para efectuar esta intersección, debemos en primer lugar reclasificar las capas de inicio de tal modo que un valor en la capa resultante defina unívocamente una única combinación de estas. Después, operaremos con las capas reclasificadas, eligiendo un operador que nos permita mantener esa correspondencia biunívoca entre pares de valores de origen y valor resultante.

Una forma de hacer esto, suponiendo un número de clases $m$ en la primera clase y $n$ en la segunda, es reclasificar la primera de ellas mediante la expresión

\begin{equation} c'_i = k^i \ ; \ k \in \mathbb{N}, i=1… m \end{equation}

donde $c'_i$ es el nuevo valor a asignar a la clase i--ésima. Es decir, se asignan potencias sucesivas de un valor natural. De igual modo, se asignan los nuevos valores a la segunda capa siguiendo la progresión de potencias, de la forma

\begin{equation} c'_i = k^{i + m} \ ; \ k \in \mathbb{N}, i=1… n \end{equation}

Con las capas anteriores, basta sumarlas para obtener una nueva en la que el valor de cada celda nos define inequívocamente a partir de qué valores originales se ha calculado.

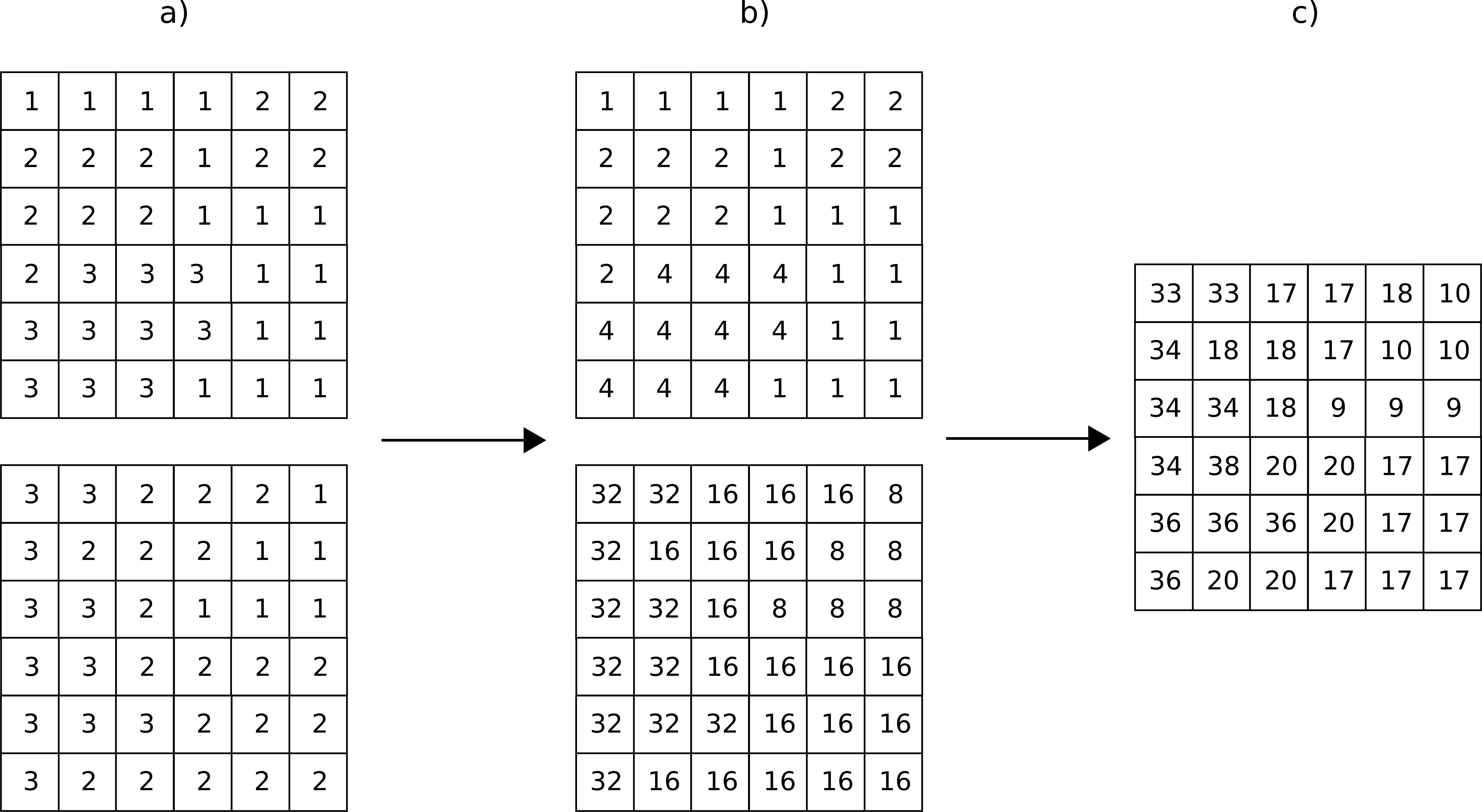
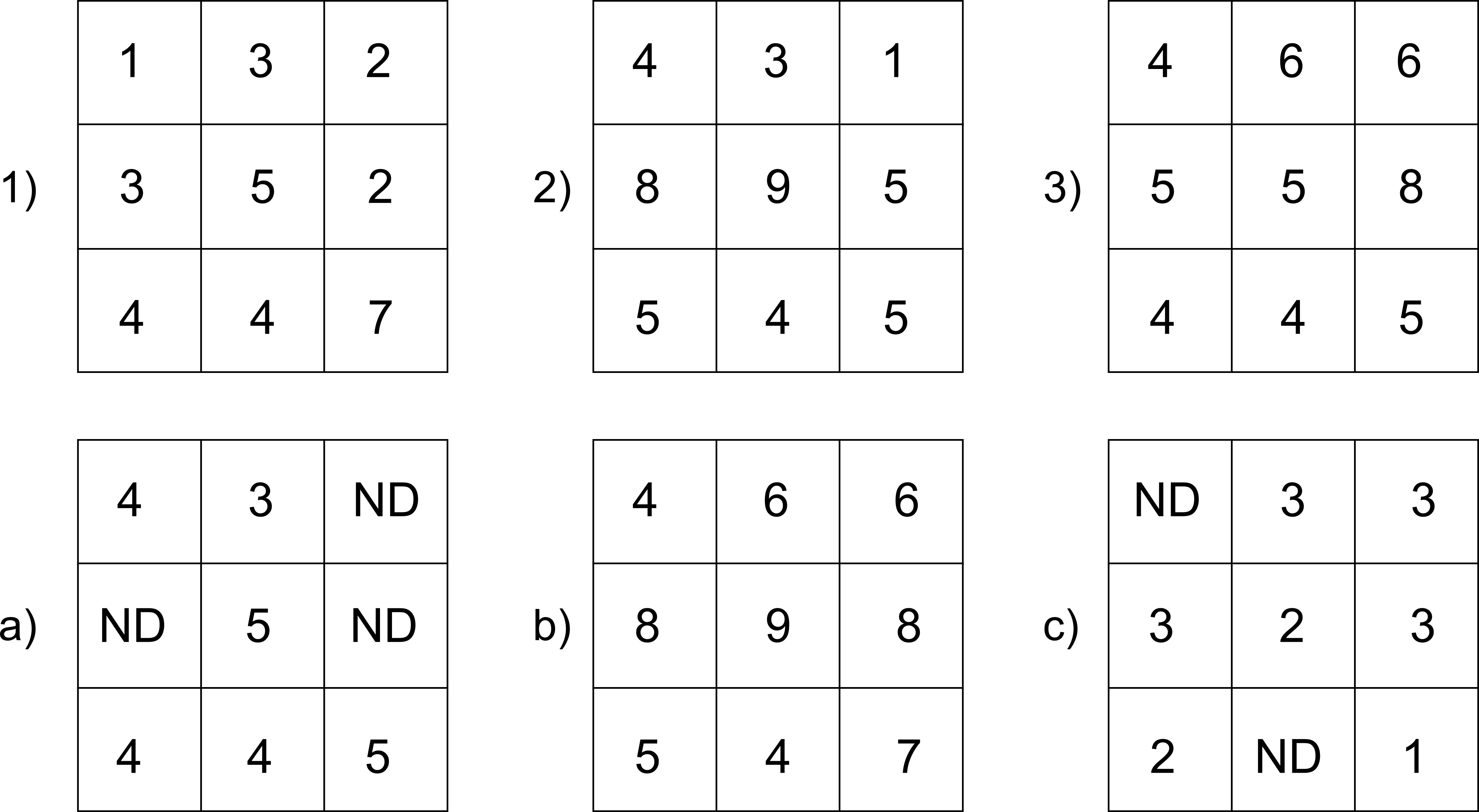
Ejemplo de combinación de dos capas categóricas. a) capas originales, b) capas reclasificadas, c) resultado.

Para ver un ejemplo que sea manejable, en la figura \ref{Fig:Combinacion_capas_categoricas_peq} se muestran dos capas con su valores originales, las capas reclasificadas según el esquema anterior, y la capa resultante.

Los SIG más comunes incorporan entre sus elementos funciones que simplifican este proceso y hacen innecesario operar de este modo, por lo que no es corriente tener que aplicar estos razonamientos manualmente. No obstante, resulta de interés el mostrar estas técnicas para estimular y desarrollar la capacidad de razonar espacial y numéricamente en base a los conceptos del álgebra de mapas, conociendo estos con detalle.

Por ultimo, para concluir esta sección es interesante señalar que la gestión de valores que representan la ausencia de datos es un aspecto importante en el empleo de operadores aritméticos en funciones locales. En general, se adopta como práctica habitual el que una operación aritmética entre celdas de varias capas devuelva un valor de sin datos siempre que alguna de las celdas implicadas carezca de datos (es decir, tenga un valor de sin datos). Dicho de otro modo, la presencia de un valor de sin datos en la operación hace que la celda resultante reciba automáticamente también valor de sin datos, particularmente el establecido para la capa resultante.

Esta forma de proceder, además de dar un resultado coherente con los datos de entrada, puede utilizarse como herramienta para, aplicando inteligentemente capas con zonas sin datos, preparar las capas de entrada de cara a su uso en otros análisis. Ese es el caso de la creación de máscaras , que nos permiten restringir la información de la capa a una parte concreta de la misma. La figura \ref{Fig:Mascara} muestra cómo un modelo digital del terreno se recorta para contener información únicamente dentro de una zona definida, en este caso todas las celdas situadas a más de 180 metros de elevación.

Para realizar el recorte, la capa que define la zona de interés contiene valor 1 en las celdas interiores y el valor de sin datos correspondiente en las exteriores. Al multiplicarlo por el modelo digital del terreno, el resultado es la propia elevación en las interiores, y el valor de sin datos en las exteriores, ya que una de las capas no tiene datos suficientes para poder generar otro resultado.

Recorte de una capa empleando una mascara con celdas sin datos. La rampa de colores se ha variado en la capa recortada para ajustarse al nuevo rango de valores de esta.

También veremos más adelante que ese uso de mascaras tiene su equivalente vectorial, existiendo una operación de recorte para capas de datos vectoriales.

Funciones focales

Las funciones de análisis focal operan sobre una sola capa de datos, asignando a cada celda un valor que deriva de su valor en la capa de partida, así como de los valores de las situadas en un entorno inmediato de esta (Figura \ref{Fig:Funciones_focales}). La función focal queda así definida por las dimensiones y forma del entorno a considerar, así como por la función a aplicar sobre los valores recogidos en este.

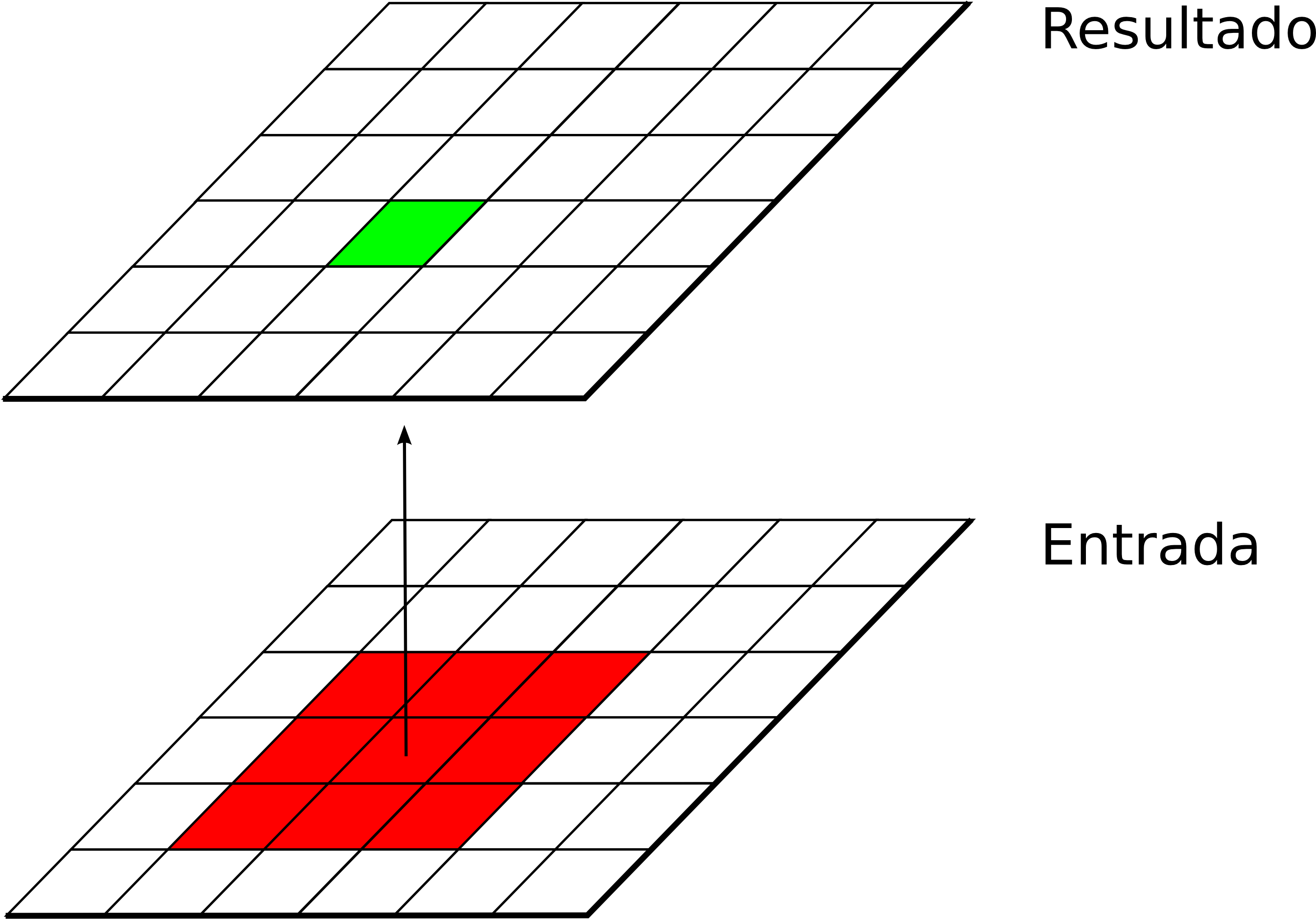
Las funciones de análisis focal analizan los valores de una celda y las situadas en un entorno de esta para obtener el valor resultante. En rojo, celdas de partida analizadas. En verde, celda que recoge el resultado.

A diferencia de las funciones locales, las focales no se aplican sobre varias capas, ya que la información necesaria se extrae de la vecindad de cada celda, dentro de la propia capa de partida.

Las funciones focales más habituales emplean un entorno cuadrado $3 \times 3$ centrado en la celda, que se va desplazando por la capa de tal modo que todas las celdas van siendo designadas como celdas centrales, y se calcula así un nuevo valor para todas ellas. Este entorno de celdas a considerar se denomina frecuentemente ventana de análisis .

Para definir las operaciones sobre esta ventana, es frecuente introducir una notación como la siguiente con el fin de simplificar las expresiones.

siendo $z_5$ la celda central, la cual recibirá el valor resultante de la operación efectuada. Puesto que los análisis focales basados en esta ventana tipo son habituales, haremos uso de esta notación en diversos puntos dentro de esta parte del libro.

Aunque menos frecuentes, pueden utilizarse ventanas de tamaño mayor, $n\times n$, siendo $n$ un valor impar para que de este modo exista un celda central. De otro modo, la ventana no podría quedar centrada sobre la celda a evaluar, sino desplazada. De igual forma, la ventana no ha de ser necesariamente cuadrada, y otras formas distintas son aplicables. La figura \ref{Fig:Tipos_ventana} muestra algunas de las más comunes, todas ellas también aplicables a distintos tamaños.

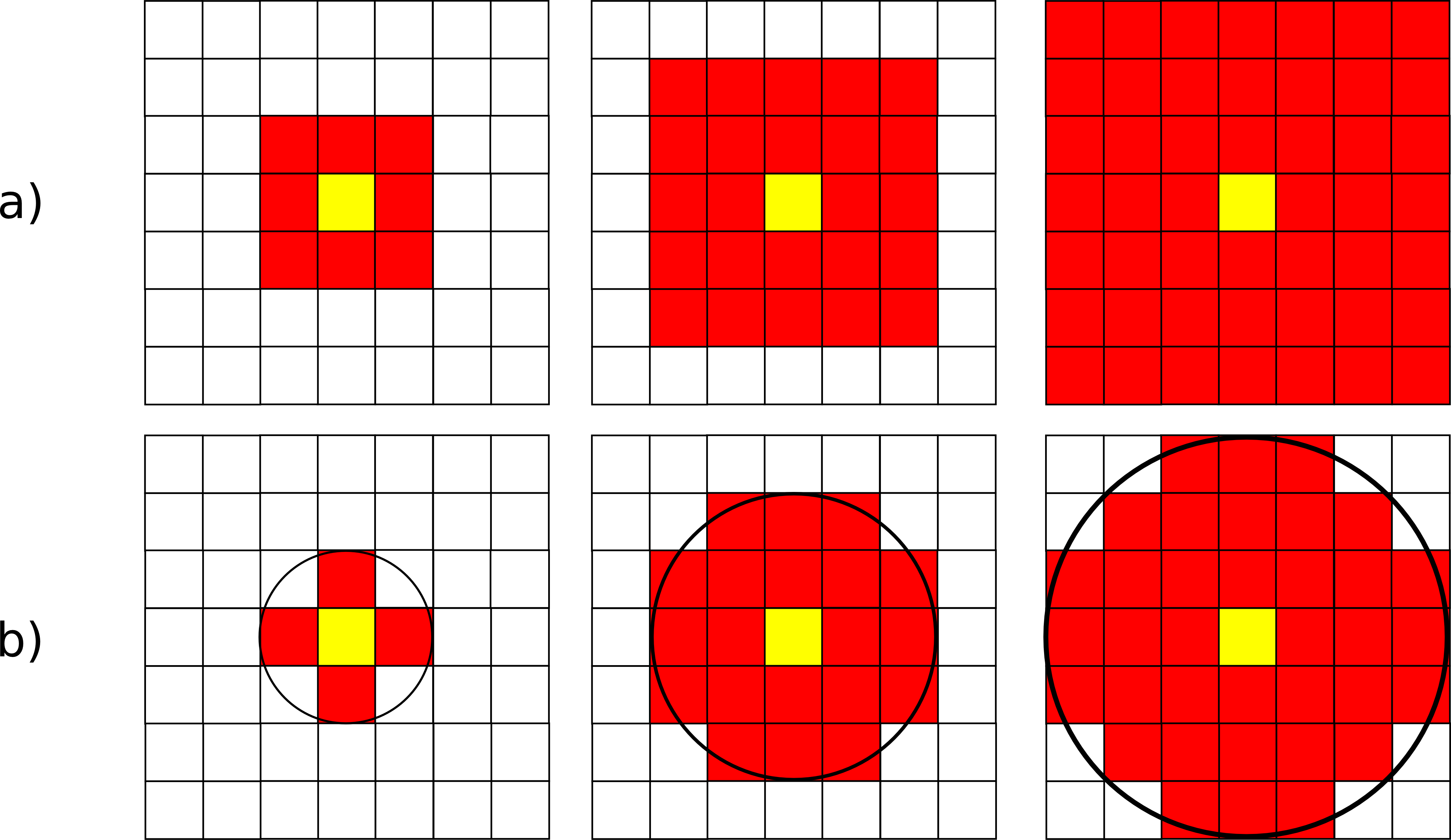
Algunos de los tipos de ventana de análisis más comunes en distintos tamaños. a) cuadrada, b) circular

Con los valores de las celdas contenidas en la ventana de análisis pueden realizarse operaciones muy diversas, entre las que cabe citar las siguientes:

Cálculo de descriptores estadísticos . Los más habituales son la media, la mediana, los valores extremos o el rango de valores. Para el caso de valores discretos, son comunes parámetros como el número de clases (número de celdas con distinto valor) dentro de la ventana de análisis.
Combinaciones lineales . De acuerdo con expresiones de la siguiente forma:
\begin{equation} \label{Eq:VentanaConvolucion} y=\frac{\sum_{i=1}^n z_i k_i}{\sum_{i=1}^n k_i} \ ; \ k_i \in \mathbb{R} \end{equation}

Este grupo particular de operaciones se conocen como convoluciones , y son la base para una larga serie de procedimientos muy comunes en el tratamiento de imágenes digitales. Es habitual expresar el conjunto de valores $k_i$ también en forma de ventana, siendo esta, lógicamente, coincidente en sus dimensiones con la de análisis. Por ejemplo, como en el siguiente caso:

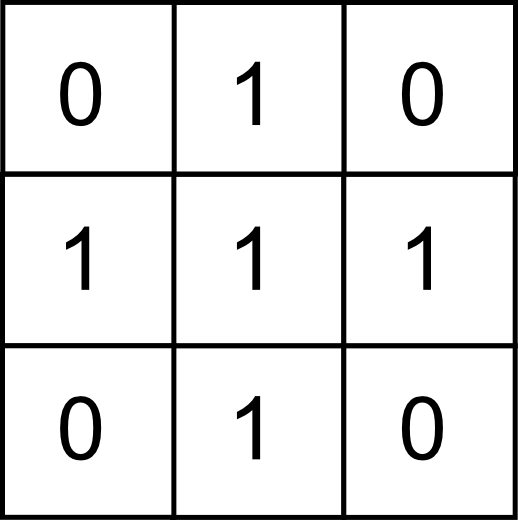
Este conjunto de valores de $k_i$ así expresados se conoce comúnmente como núcleo o kernel de la convolución. Nótese que el núcleo anterior se corresponde con el cálculo de la media aritmética, pudiendo expresarse este descriptor estadístico como una combinación lineal de los valores de la ventana, a través de un núcleo.
Operaciones matemáticas de forma general . No necesariamente combinaciones lineales, aplican operadores más complejos a los valores de la ventana.
Clasificaciones . En función de la configuración de los valores dentro de la ventana clasifican la celda en una serie de posibles grupos, de acuerdo con unas reglas definidas. El resultado es una capa de información discreta, frente a las anteriores que producen capas continuas. Un ejemplo de esto lo encontramos en la clasificación de formas de terreno, la cual veremos en el apartado Caracterizacion_terreno , o en la asignación de direcciones de flujo según el modelo D8 ( Direcciones_flujo ).

Algunas de las funciones anteriores se han de definir de forma específica para un tamaño y forma de ventana dado, mientras que otras, como el caso de los descriptores estadísticos, pueden definirse de forma genérica. La diferencia estriba en que en estos la posición del valor dentro de la ventana de análisis no es relevante, mientras que para otras funciones sí lo es.

El resultado de un operador de análisis focal no ha de ser necesariamente un valor que se sitúa en la celda central de la capa resultante una vez ha sido calculado. Por ejemplo, y relacionado con lo comentado en el párrafo anterior, [ Caldwell2000GeoComputation ] propone un operador que, evaluando los valores dentro de la ventana de análisis, modifique la capa de salida no en la celda central, sino en aquella.que cumpla una condición dada. Por ejemplo, aquella que contenga el valor máximo de entre todas las de la ventana. Lo importante en este caso no es el valor, sino sobre qué celda se sitúa.

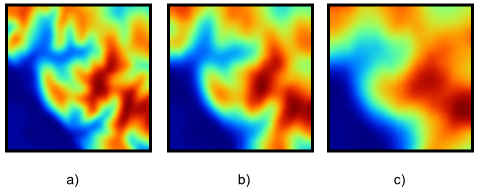
Con respecto al tamaño de la ventana de análisis, debe mencionarse que la utilización de uno u otro tiene dos consecuencias directas: por un lado el proceso es más costoso en términos de tiempo a medida que aumentamos la ventana, ya que el número de celdas a analizar es mayor. Por otro, el resultado puede diferir notablemente, y es necesario tener en cuenta el significado del parámetro a calcular para establecer unas dimensiones correctas —dimensiones en unidades reales, no en número de celdas— de la ventana. La figura \ref{Fig:Comparacion_tamanos_ventana} muestra cómo el efecto de un filtro de media, el cual produce un desenfoque de la imagen, se hace más patente a medida que empleamos ventanas de análisis mayores.

En [ Wood1996PhD ] puede encontrarse información adicional sobre la noción de escala de análisis —especialmente para el caso de análisis del terreno— y otros conceptos íntimamente relacionados con la elección de un tamaño de ventana. En el apartado Caracterizacion_terreno veremos un análisis particular en el que la elección del tamaño de ventana es particularmente importante.

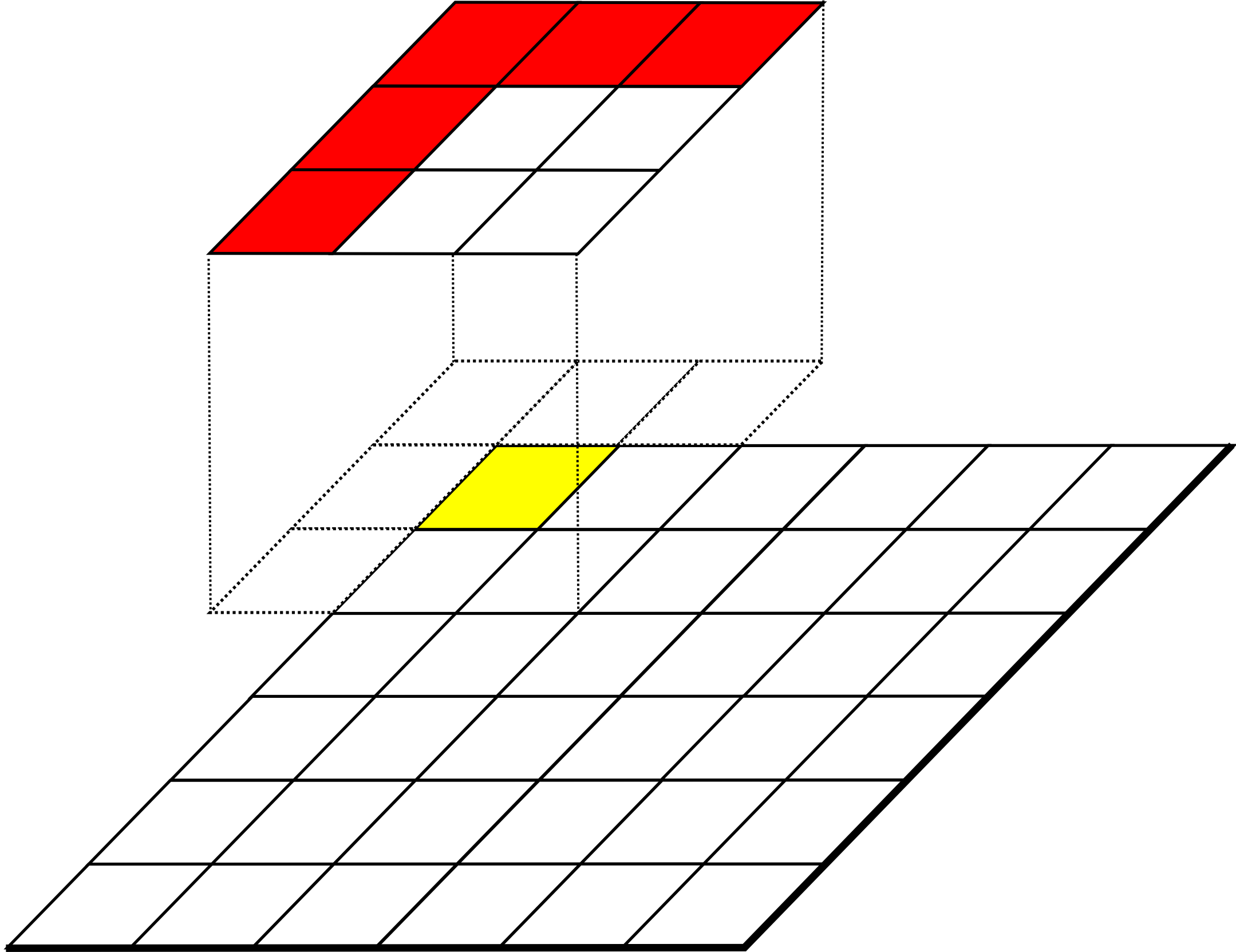
Resultados de un filtro de mediana sobre una imagen para distintos tamaños de ventana. a) $5\times5$, b) $10\times10$ c) $20\times20$

Con independencia de dicho tamaño de ventana, siempre vamos a tener algunas celdas para las que esta no va a poder definirse en su totalidad. Estas celdas son las situadas en los bordes de la capa, ya que en su caso siempre habrá algunas celdas de la ventana que caigan fuera y para las cuales no tengamos un valor definido (Figura \ref{Fig:Analisis_focal_bordes}). En este caso, debe o bien definirse una nueva formulación para estas celdas de borde, o trabajar únicamente con las celdas interiores a la capa, o directamente asignar un valor de sin datos a la capa resultante, indicando que no puede evaluarse el parámetro en ausencia de algún dato. El optar por una u otra alternativa será función, como ya vimos antes, de si el valor resultante depende o no de la posición de los valores de partida.

En las celdas de borde la ventana de análisis no puede definirse en su totalidad. Las celdas en rojo representan celdas fuera de la capa para las cuales no existe información

Para el caso de una media aritmética, si de los nueve valores de la ventana habitual solo tenemos, por ejemplo, seis, podemos operar con ellos y asumir que el resultado será satisfactorio. En el caso de asignar direcciones de flujo, sin embargo, los valores pueden ser erróneos, ya que tal vez el flujo se desplace hacia las celdas fuera de la capa, pero al faltar la información de estas, no será posible hacer tal asignación. Una práctica recomendable en cualquier caso es no limitar la extensión de la capa a la mínima que englobe el área del territorio que queramos estudiar, sino tomar una porción adicional alrededor para que estos efectos de borde no tengan influencia sobre nuestro estudio.

Funciones zonales o regionales

Las funciones de análisis zonal asocian a cada celda valores relativos no a ella misma ni a un entorno fijo alrededor, sino a la clase a la que dicha celda pertenece (Figura \ref{Fig:Funciones_zonales}). Se necesita, por tanto, una capa de apoyo que contenga la pertenencia de cada celda a una u otra clase, ya que la utilización de una celda en el análisis no se establece por posición, como en los casos anteriores, sino por valor. Esta capa es de tipo discreto y representa una teselación del territorio en un número definido de clases.

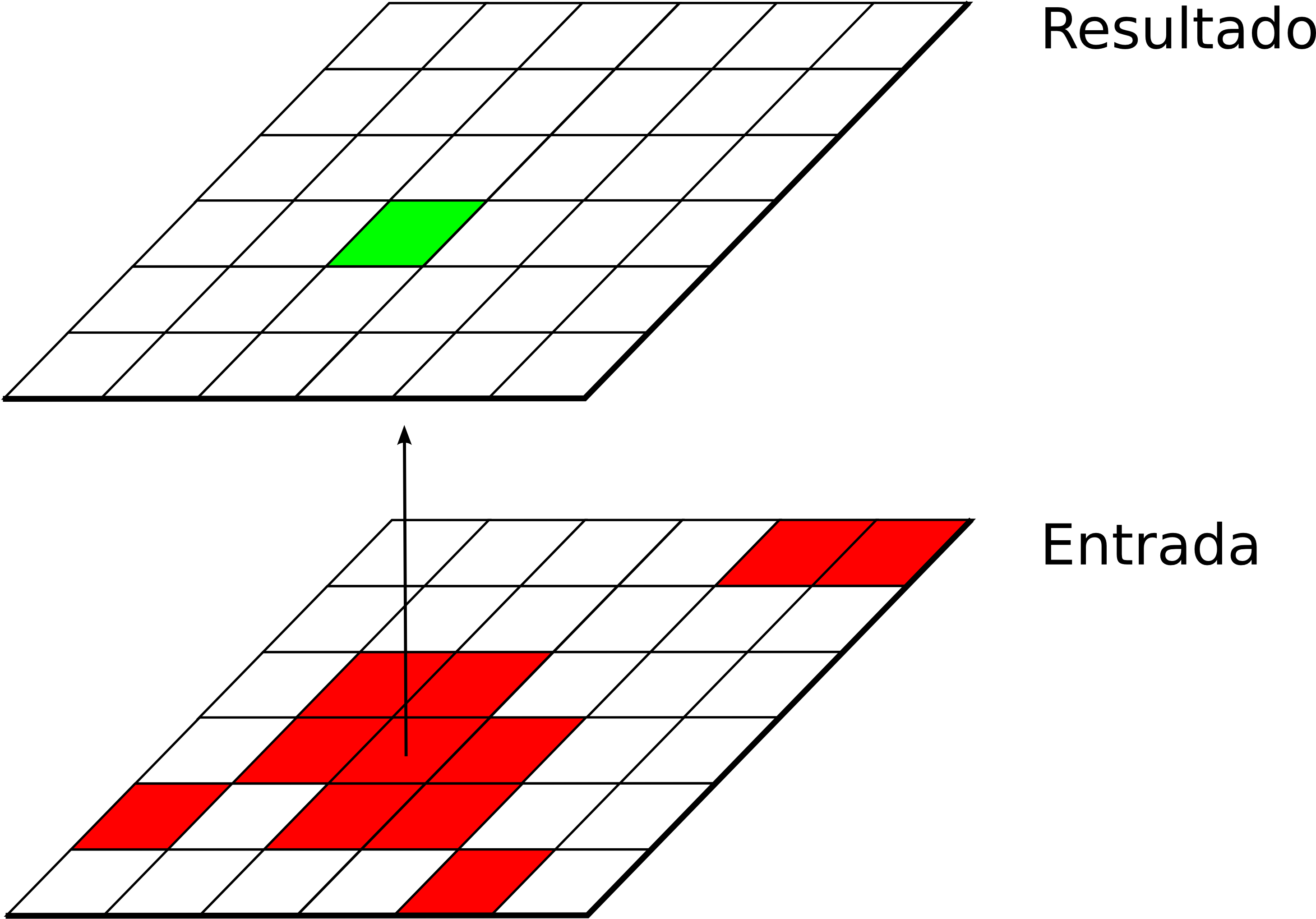
Las funciones de análisis zonal analizan los valores de todas las celdas asociadas a una misma clase cada para obtener el valor resultante. En rojo, celdas de partida analizadas. En verde, celda que recoge el resultado.

Lo habitual es emplear esta capa de clases en conjunción con otra, ya sea de valores continuos o discretos, y extraer de esta segunda los valores a utilizar para definir el valor representativo de cada clase. Ese es el caso del ejemplo propuesto al principio del capítulo, donde se utiliza el mapa de pérdidas de suelo para asignar los valores correspondientes a cada subcuenca. En este caso, las clases vienen definidas por las subcuencas.

La definición del conjunto de celdas relacionadas con una dada puede realizarse de dos formas distintas (Figura \ref{Fig:Definicion_clases}):

Todas las celdas con el mismo valor que la celda problema, conectadas por contigüidad con esta.
Todas las celdas con el mismo valor que la celda problema presentes en la capa, con independencia de su conexión.

Formas de definir las clases para el análisis zonal. En verde, celda de análisis. En rojo, celdas a considerar en su misma clase para ser empleadas en el cálculo. a) asignación por valor con contigüidad, b) asignación únicamente por valor.

En el caso de las pérdidas por subcuencas, calculábamos con los valores del conjunto de celdas pertenecientes a cada clase su media aritmética, pero pueden aplicarse igualmente diversos descriptores estadísticos o funciones más complejas, al igual que ya vimos en los otros tipos de funciones.

Los valores a asignar a cada clase pueden extraerse también de la propia capa de clases, no siendo necesaria otra capa. En este caso, estos valores resultantes suelen tener relación no con un parámetro adicional, sino con la geometría de cada clase. Por ejemplo, la superficie o el perímetro de cada tesela pueden recogerse como valores asociados a esta.

Este es un tipo de análisis muy frecuente en el estudio del paisaje, y el número de parámetros que pueden obtenerse por análisis zonal a partir de una única capa de clases es muy elevado. Junto a parámetros sencillos como la citada superficie o el perímetro, otros parámetros más complejos pueden servir para recoger la configuración estructural de las teselas, su riqueza y variabilidad, la fragmentación, etc [ referenciaFragstats ].

Funciones globales

Las funciones globales son aquellas que utilizan la totalidad de valores de la capa para la obtención del resultado (Figura \ref{Fig:Funciones_globales}). Por su forma de operar, no generan exclusivamente nuevas capas como las anteriores funciones, sino tanto valores concretos como objetos geográficos de diversa índole.

Las funciones de análisis global analizan el conjunto de valores de una capa para obtener un valor resultante, que puede ser tanto un objeto geográfico (capa ráster o vectorial) como un valor escalar sencillo, una tabla u otro tipo de resultado.

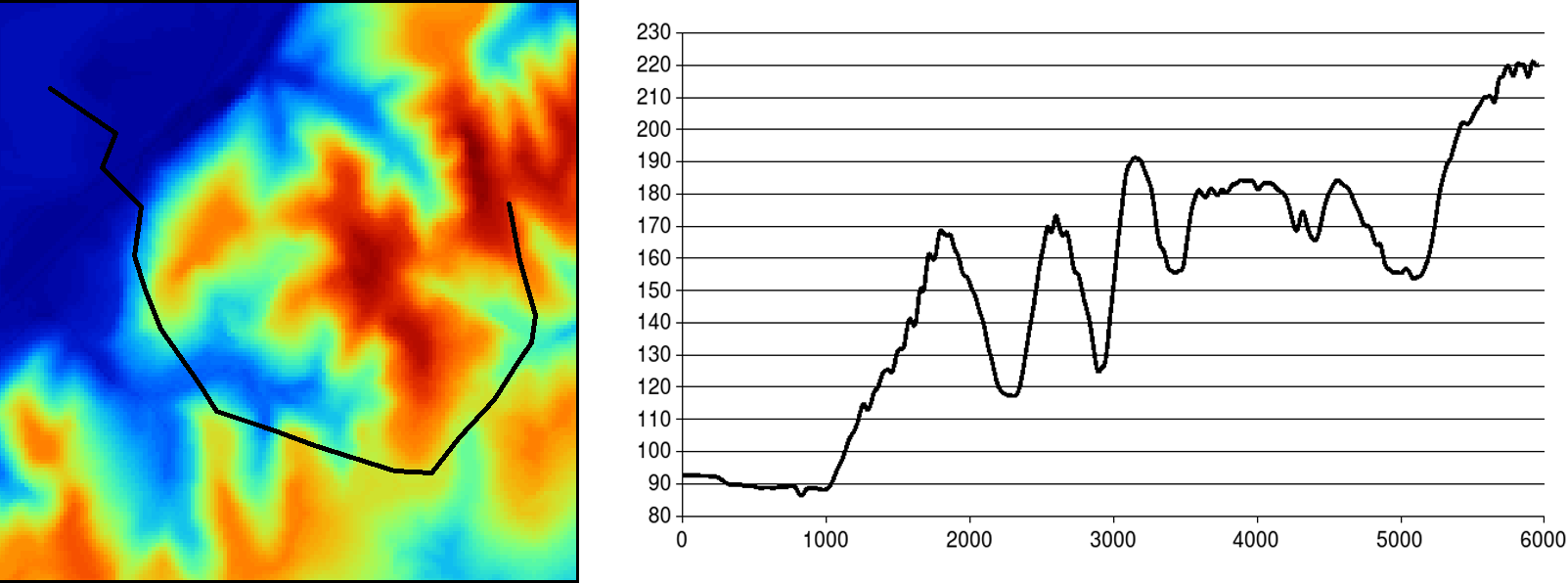
Por ejemplo, los valores máximo y mínimo de la capa que son necesarios para normalizar esta se obtienen mediante una función global. Asimismo, el cálculo de un perfil entre dos puntos (Figura \ref{Fig:Perfil}) o el trazado de una ruta óptima sobre una superficie de coste acumulado (que veremos en el apartado Rutas_optimas ) son ejemplos de funciones globales que generan un resultado distinto de un mero valor numérico.

Dada una ruta y una capa, podemos obtener un perfil de valores a lo largo de la ruta mediante una función global.

En el apartado dedicado a las funciones locales veíamos cómo la aplicación del operador distinto de entre dos capas de uso de suelo correspondientes a distintas fechas nos servía para localizar las zonas que habían experimentado cambios en su uso de suelo. Tras esta operación, la capa resultante contendrá un valor verdadero , habitualmente representado con un 1, en las zonas donde se da esa variación, y falso , codificado con 0, en las restantes. Si queremos cuantificar esa variación, podemos aplicar un operador global que sencillamente sume los valores de todas las celdas de la capa, lo cual dará como resultado el número total de celdas cuyo uso de suelo ha variado en el periodo de tiempo comprendido entre las dos fechas representadas por las capas de entrada.

Puesto que los operadores globales operan sobre la totalidad de la capa, a veces resulta conveniente o incluso necesario «eliminar» de esta los valores que no son de interés para el cálculo. No debemos olvidar que una capa ráster tiene una forma rectangular, la cual raramente se va a corresponder con la de la región de análisis, ya sea esta definida por un limite natural o no. El uso de máscaras que vimos en Funciones_locales es muy práctico a estos efectos.

Considérese, por ejemplo, que una curva hipsográfica que representa la distribución de alturas dentro de un área dada (habitualmente una unidad hidrológica), no tiene mucho sentido si se aplica a una región delimitada de forma «artificial» por los límites rectangulares de la capa. Resulta más lógico aplicar una máscara sobre la capa a analizar, de modo que la función global ignore las celdas que, aun estando en la capa, no están en la unidad de interés. Estas celdas tendrán asociado un valor de sin datos tras la aplicación de dicha máscara.

Preparación de capas

Las variables que manejamos en el álgebra de mapas son, como hemos visto en los ejemplos precedentes, capas ráster y valores escalares que podemos combinar con los anteriores. Para algunas de las funciones resulta necesaria únicamente una capa, mientras que para otras son necesarias varias.

En los ejemplos que hemos visto de combinación de varias capas, hemos dado siempre por supuesto que todas ellas tienen una estructura común. Es decir, que cubren una misma porción de terreno y lo hacen mediante una malla de celdas de las mismas dimensiones, con un mismo tamaño de celda y una misma georreferenciación. De este modo, un punto del terreno con coordenadas dadas queda reflejado en todas las capas en la misma celda $i,j$, y podemos operar con sus valores directamente para obtener un resultado correspondiente a dicho emplazamiento.

No obstante, a la hora de combinar capas es muy frecuente que estas tengan procedencias distintas y esta circunstancia no se dé. En tal caso, hay que preparar las capas para adecuarlas a un mismo marco geográfico sobre el que aplicar las funciones del álgebra de mapas de forma adecuada. Si este marco consiste en una malla de celdas de dimensiones $n\times m$, y las coordenadas de cada celda $i,j$ son respectivamente $x_{ij}$ e $y_{ij}$, deben calcularse los valores de las capas en esas coordenadas a partir de los valores en los marcos de referencia originales. Este proceso se denomina remuestreo .

El remuestreo en realidad es una interpolación similar a la que veíamos en el capítulo Creacion_capas_raster , con la diferencia de que en este caso los puntos con datos no están distribuidos irregularmente sino de forma regular en una malla, con lo que podemos dar una expresión para la función interpolante en función de las celdas de origen situadas en torno a la coordenada en la que queremos calcular el nuevo valor (la del centro de cada celda en la capa remuestreada).

Los métodos más habituales de remuestreo son los siguientes:

Por vecindad . Como ya vimos, no se trata en realidad de una interpolación como tal, pues simplemente crea la nueva malla situando nuevas celdas cuyos valores se calculan por mera vecindad, tomando el de la celda más cercana.
Bilineal . Para una celda $(i',j')$ en la nueva malla interpolada, su valor en función de los de las $4$ celdas más cercanas a la misma en la malla original viene dado por la expresión.
\begin{eqnarray} z_{(i',j')}&=&z_{(i,j)}R(-a)R(b)\nonumber\\ & & +z_{(i,j+1)}R(a)R(-(1-b)) \nonumber \\ & & +z_{(i+1,j)}R(1-a)R(b) \nonumber \\ & & +z_{(i+1,j+1)}R(1-a)R(-(1-b))\nonumber\\ \end{eqnarray}

donde $R(x)$ es una función triangular de la forma

\begin{equation} R(x) = \left \{ \begin{array}{ll} x+1 & \textrm{ si } -1\leq x \leq 0 \\ 1-x & \textrm{ si } -0\leq x \leq 1 \\ \end{array}\right. \end{equation}
Interpolación bicúbica . La interpolación bicúbica es un método de interpolación multivariante bidimensional que emplea un polinomio de tercer grado para cada una de las direcciones. Son necesarias $16$ celdas en lugar de las $4$ de la bilineal, lo que hace que el método sea más exigente en términos de proceso. Para el caso habitual de emplear como función interpolante un spline cúbico, se tiene \begin{eqnarray} z_{(i',j')}&=&\sum^2_{m=-1}\sum^2_{n=-1}(z_{(i+m,j+n)}R(m-a)\nonumber\\ && \cdot R(-(m-b))) \end{eqnarray}
\begin{eqnarray} R(x)&=&\frac{1}{6}((x+2)^3_+-4(x+1)^3_+\nonumber\\&&+6(x)^3_+-4(x-1)^3_+) \end{eqnarray} siendo \begin{equation} (x)^m_+ = \left \{ \begin{array}{ll} x^m & \textrm{ si } x > 0 \\ 0 & \textrm{ si } x \leq 0 \\ \end{array}\right. \end{equation}

Los métodos de remuestreo son un área muy desarrollada en el tratamiento de imágenes digitales, aunque, en la práctica, la mayoría de algoritmos existentes no presentan una diferencia notable con los anteriores (excepto con el remuestreo por vecindad) a la hora de aplicarlos sobre capas ráster de variables continuas en lugar de imágenes. Es por ello que su implementación y uso no es habitual en el caso de los SIG. En [ Turkowski1990Gems ] puede encontrarse una buena introducción a otro tipo de funciones utilizadas para el remuestreo de imágenes.

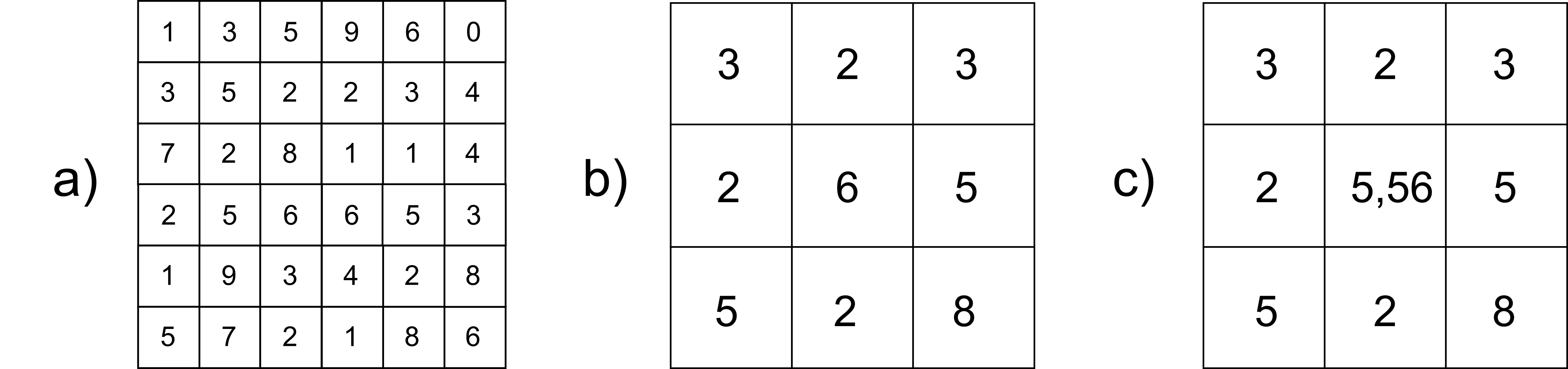
El remuestreo de capas categóricas solo puede llevarse a cabo por vecindad. a) capa original, b) remuestreo por vecindad, c) remuestreo mediante splines (incorrecto, con valores incoherentes)

A la hora de elegir uno u otro de los métodos anteriores, debe tenerse en cuenta, fundamentalmente, el tipo de información que contenga la capa. Una diferencia fundamental que debe tenerse siempre presente es que, de entre los métodos anteriores, el de vecino más cercano es el único que garantiza que los valores resultante existen como tales en la capa origen. Ello hace que este sea el único método que puede utilizarse a la hora de remuestrear capas de información categórica. Podemos ver claramente esto en la figura \ref{Fig:Tipos_remuestreo}. Se aprecia que en la capa remuestreada mediante interpolación bicúbica aparece un valor no entero producto de las operaciones matemáticas aplicadas, frente a los valores enteros que representan las categorías en la capa original. Los valores no enteros carecen de sentido, y hacen así que la capa remuestreada no sea válida.

Incluso si no apareciesen valores decimales, el remuestreo de capas categóricas por métodos distintos del vecino más cercano es conceptualmente incorrecto, ya que la realización de operaciones aritméticas con valores arbitrariamente asignados a las distintas categorías carece por completo de sentido.

Cuando se trabaje con imágenes directamente, es de interés el considerar esta misma circunstancia referente a los métodos de remuestreo aplicables en relación con la interpretación de la imagen que vaya a llevarse a cabo. La aplicación del remuestreo por vecindad es en la mayoría de los casos la opción a elegir, en especial cuando se va a proceder a un análisis de la imagen con posterioridad.

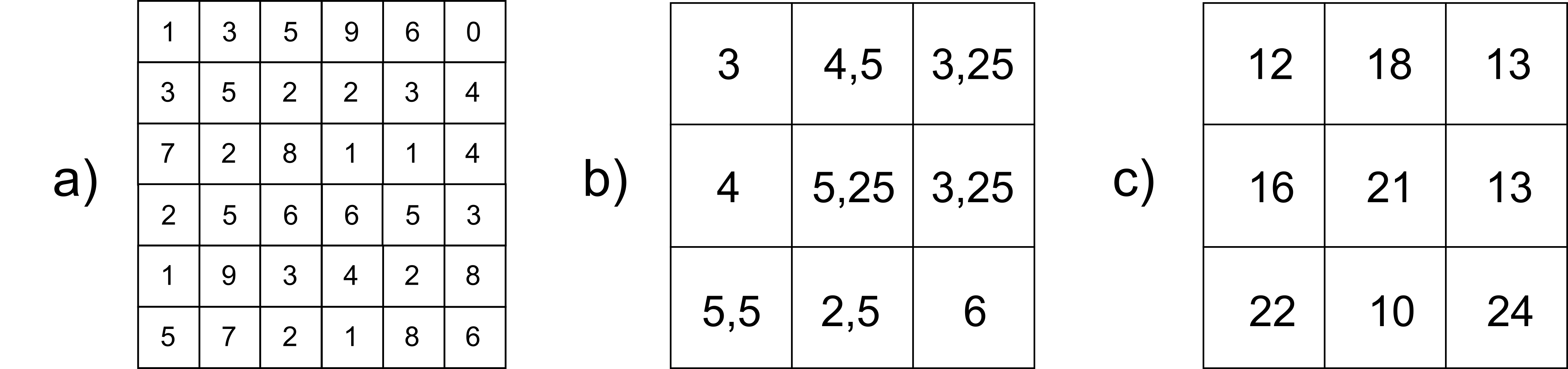
Aun en los casos de variables no categóricas, y aunque la elección del método de remuestreo no conduce de por sí a un resultado necesariamente erróneo, el proceso de remuestreo como tal sí que puede hacerlo si no se razona en función de la información contenida en la capa. Podemos ver esto claramente en el ejemplo de la figura \ref{Fig:Remuestreo_conteo}.

La capa original contiene información sobre el número de individuos de una especie que han sido encontrados en cada celda, de tal modo que representa la densidad de dicha especie. Si se modifica el tamaño de celda para hacerlo el doble de grande, la nueva celda tras el remuestreo cubre cuatro celdas de la capa original. Mientras que el remuestreo asignará a esa celda un valor promedio de las cuatro originales que engloba, el numero de individuos en ella será realmente la suma de ellos. Debe aplicarse un factor de reescala que relacione el área de la celda antes del remuestreo con el tamaño después del mismo, para así mantener la coherencia en el significado de la variable.

Dependiendo de la variable recogida en la capa, el proceso de remuestreo puede requerir operaciones adicionales para obtener un resultado correcto. a) capa con valores de conteos (número de individuos) por celda para una especie dada, b) capa tras remuestreo (incorrecta), c) capa tras remuestreo y aplicación de factor de reescala (correcta)

Extensión del álgebra de mapas

Aunque en la práctica los conceptos definidos por Tomlin son la base para la implementación genérica de algoritmos, diversos autores han intentado extender estos conceptos y formalizarlos de una forma más general. Aunque tratar estos sistemas escapa al alcance de este texto, resulta de interés mencionar algunas de las propuestas.

[ Camara2005SimpoBras ] propone un nuevo álgebra de mapas al que se incorporan predicados topológicos y direccionales. Esta definición permite la realización de operaciones que el álgebra de Tomlin no contempla, ya que, como demuestran, es un caso particular del anterior.

La propuesta de [ Takeyama1997IJGIS ] con su geo--álgebra es distinta, y se encamina a una formalización matemática completa de las operaciones espaciales. En ella, no solo se contemplan los datos espaciales, sino también los procesos existentes. Así, se extiende no solo el álgebra de operaciones, sino el concepto de mapa a través de los nuevos conceptos de mapa relacional y meta--relacional . La integración de modelos basados, por ejemplo, en autómatas celulares, es posible dentro del marco de este geo--álgebra

Por último, y aunque no relacionada directamente con la información geográfica, el álgebra de imágenes definida por [ Ritter1990CompuVision ] guarda una gran similitud debida a la parecida naturaleza de los datos ráster y las imágenes como ya hemos comentado. Este álgebra de imágenes pretende establecer una notación algebraica con la cual expresar los algoritmos del procesado de imágenes, muchos de los cuales comparten una base conceptual común con los empleados en el análisis geográfico, y que veremos en el capítulo Procesado_imagenes .

Resumen

El álgebra de mapas nos proporciona las herramientas necesarias para analizar capas ráster y obtener de ellas resultados derivados. Bien sea a partir de una capa, de dos, o de una batería de ellas, las funciones del álgebra de mapas definen un marco formal de procesos dentro del cual desarrollar los más diversos análisis. Distinguimos cuatro tipos básicos de funciones: locales, focales, zonales y globales.

De cada uno de ellos veremos numerosos ejemplos de aquí en adelante, ya que constituyen la base conceptual sobre la que se construyen la práctica totalidad de algoritmos de análisis de capas ráster. Estas funciones han de ir unidas a un manejo adecuado de las variables de entrada (las capas ráster), así como a una serie operadores que se aplican sobre las celdas que cada función define como objeto de análisis.