Análisis espacial. Fundamentos

El análisis espacial es una de las tareas fundamentales sin las cuales el concepto de SIG no alcanza su verdadero significado.

El análisis espacial es el estudio cuantitativo de aquellos fenómenos que se manifiestan en el espacio. Ello indica una importancia clave de la posición, la superficie, la distancia y la interacción a través del propio espacio.

Ejemplos de análisis que realizamos con cartografía fuera de un SIG son el buscar en un mapa dónde se sitúa el pico más alto, ver la elevación concreta a la que se encuentra un elemento dado tal como una población, o planificar una jornada turística viendo qué lugares de interés podemos visitar o cómo llegar desde uno a otro de estos lugares haciéndolo por las mejores carreteras o de la forma más rápida. Estas actividades habituales son ejemplos de análisis geográficos que podemos igualmente realizar dentro de un SIG.

Mediante el análisis podemos generar nuevos datos que pueden ser nuevas capas de datos geográficos, tablas de datos, valores escalares o vectores.

En ocasiones, los resultados expresan la misma variable que el dato de partida (por ejemplo, el cálculo de una media), y en otros las variables de entrada y salida son distintas (por ejemplo, si a partir de una capa de elevaciones calculamos una de pendientes).

Asimismo, todo análisis espacial parte de un conjunto de datos espaciales, pudiendo estos ser de un único tipo, o de varios distintos que se combinan en un procedimiento concreto. Por ejemplo, en el caso de calcular la localización del punto más alto, el resultado es una sencilla coordenada, y tan solo se utiliza la variable elevación. En el caso de la altura media de una ciudad, se utilizan dos entradas: por un lado, la elevación, y por otro, el emplazamiento de la ciudad. Aunque un mapa clásico contiene toda esa información en una única hoja, en realidad son dos elementos distintos combinados a la hora de representarlos. En términos más acordes con un SIG, podemos decir que tenemos dos capas distintas que utilizamos como entradas.

El análisis dentro un SIG nos permite tanto formular como responder a cuestiones. Estas cuestiones pueden ser:

• Relativas a posición y extensión
• Relativas a la forma y distribución
• Relativas a la asociación espacial
• Relativas a la interacción espacial
• Relativas a la variación espacial

Algunos ejemplos de análisis espacial

Algunos ejemplos de análisis espacial son los siguientes.

Consulta espacial

Vimos las consultas en detalle dentro del capítulo dedicado a las bases de datos.

Pueden combinarse con otros de los análisis disponibles, por ejemplo para la selección de una serie de elementos sobre los que posteriormente se desarrollara el análisis en cuestión.

Análisis topológico

Pueden plantearse consultas referidas no solo a la posición de los elementos geográficos, sino a la relación con otros elementos. La existencia de topología puede emplearse para la realización de consultas que respondan a cuestiones como:

• ¿Cómo llegar desde mi posición actual hasta una coordenada concreta por la red viaria existente?

• ¿Qué comunidades autónomas comparten límite con Madrid?

Medición

La existencia de una referencia espacial para cada uno de los elementos con los que trabajamos en el análisis dentro de un SIG hace que podamos cuantificar otra serie de parámetros también espaciales. Entre las mediciones más básicas, encontramos las distancias, áreas, perímetros o factores de forma. Mas elaboradas, encontramos otras como pendientes o indices derivados de medidas simples.

Combinación

Uno de los procedimientos más habituales y más característicos dentro del uso de un SIG es la combinación o superposición de varias capas de información. La propia estructura de la información geográfica en capas facilita notablemente estos procedimientos y convierte a los SIG en plataformas ideales para llevar a cabo análisis donde se combina información sobre diversas variables.

En el caso de capas vectoriales, las operaciones de solape tales como unión, intersección, diferencia o recorte, son habituales. La figura 9.1 muestra un ejemplo de la operación de intersección con dos capas de polígonos.

Transformaciones

Podemos englobar dentro de este grupo una amplia serie de procedimientos que modifican los elementos de entrada de diversas formas. Entre los más habituales, encontramos la transformación de coordenadas, la simplificación de geometrías, o la creación de áreas de influencia o la reclasificación de valores. Estas transformación pueden afectar tanto a la componente espacial como a la componente temática del dato.

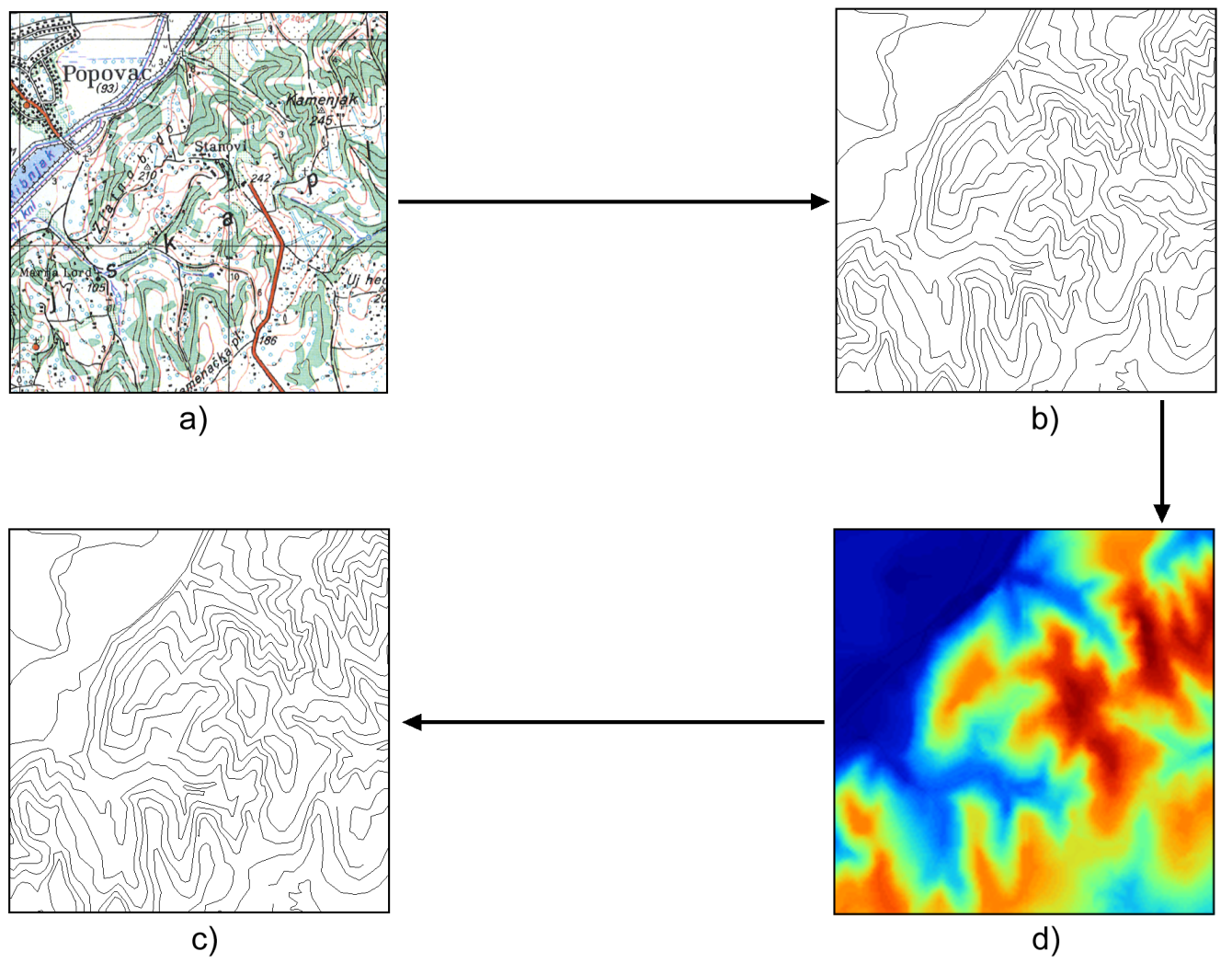
Un caso particular, ya mencionado en un capítulo anterior, es la conversión entre modelos de datos, esto es, entre el modelo ráster y el vectorial. La figura 9.2 muestra un ejemplo de esto. Partiendo de un mapa escaneado (una capa ráster) con curvas de nivel, pueden detectarse estas y crearse una capa vectorial con dichas curvas de nivel. Estas pueden posteriormente convertirse en un Modelo Digital de Elevaciones (ráster) mediante interpolación, el cual es posible convertir de nuevo en una capa vectorial de líneas.

Análisis de superficies

El análisis de superficies es uno de los más potentes de cuantos encontramos en un SIG. Desde parámetros básicos como la pendiente o la orientación hasta parámetros morfométricos muy específicos, pasando por todas las herramientas del análisis hidrológico, la batería de operaciones disponibles es muy amplia.

Estadística descriptiva

Los elementos de la estadística clásica tienen sus equivalentes en los datos espaciales, y nos permiten calificar cuantitativamente los datos con los que trabajamos. Se incluyen aquí descriptores de centralidad y dispersión, de dependencia espacial o el estudio de patrones espaciales, entre otros muchos. Estos pueden a su vez usarse para el contraste de hipótesis que contengan una cierta componente espacial.

Por ejemplo, estos estadísticos nos permiten dar respuesta a cuestiones del tipo:

• ¿Es constante la media de altura a lo largo de toda la geografía de mi país?

• ¿Existe alguna dirección predominante en los movimientos de individuos de una especie o se desplazan erráticamente?

Inferencia

Otro análisis estadístico de gran importancia en los SIG es el que permite inferir comportamientos de las distintas variables y estudiar, por ejemplo, la forma en que estas van a evolucionar a lo largo del tiempo.

El establecimiento de modelos de cambio y variación representa una de las herramientas más actuales en el campo de los SIG, y un campo en abundante desarrollo.

Toma de decisiones y optimización

La estructura de la información geográfica en capas dentro de un SIG, favorable como ya vimos para la superposición de capas, lo es igualmente para estudiar de forma combinada los efectos de distintos factores. Este estudio nos permite luego responder a cuestiones como, por ejemplo:

• ¿Cuál es el mejor lugar para emplazar una nueva construcción en función de su impacto sobre el medio?

• ¿Dónde situar un nuevo hospital para que el servicio en la comarca mejore lo máximo posible?

Modelización

La creación de modelos espaciales dentro de un SIG es una tarea aún pendiente de mucho desarrollo. No obstante, existe un gran número de modelos en los más diversos campos, y la arquitectura de datos y procesos de los SIG es propicia para la implementación de otros nuevos.

Particularidades de los datos espaciales para su análisis

Las características propias de los datos espaciales dotan a estos de una gran potencialidad de análisis, al tiempo que condicionan o limitan otras operaciones. Algunas de estas características representan problemas que han de tenerse presentes en el análisis; otros son simplemente conceptos básicos que deben conocerse pero no han de implicar necesariamente una dificultad asociada.

Escala

A la hora de estudiar la información geográfica, podemos hacerlo a distintos niveles y, dependiendo del nivel elegido, los resultados serán de una u otra naturaleza. Debido a esto, además de considerar la escala cartográfica para la representación y gestión de datos en un SIG, es necesario considerar la escala de análisis.

La escala de análisis depende del dato en sí (precisión, tipo, etc.), así como del análisis que se va a realizar con él.

Como se muestra en la figura 9.3, si para definir las formas de relieve en un punto dado lo hacemos considerando dicho punto y los valores de elevación a su alrededor, la caracterización que hagamos varía en función de la dimensión de esa zona alrededor (que es la que define la escala de análisis). Para valores pequeños de dicha zona de análisis, el punto analizado puede definirse como una cima, mientras que aumentando la escala de análisis se advierte que el punto se sitúa en el fondo de un valle.

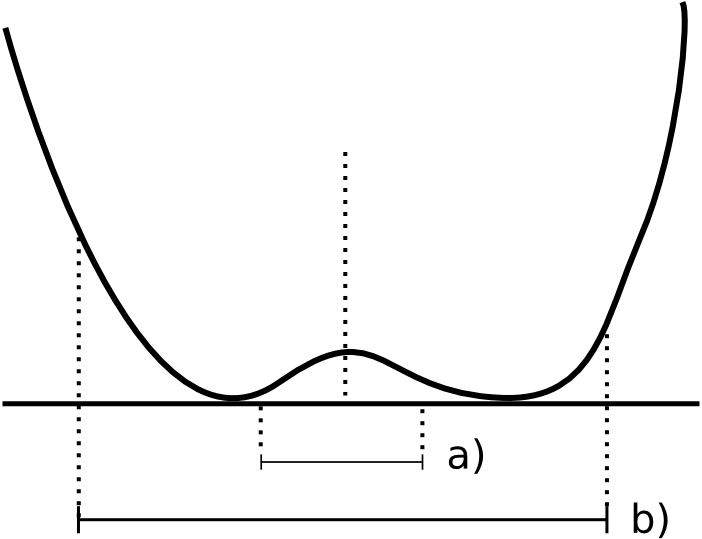
Por tanto, debemos observar el relieve desde la distancia correcta a la cual la información que nos proporciona es la más adecuada para un análisis dado. Además de existir una escala de mayor relevancia para un análisis concreto, es de interés el trabajar a múltiples escalas y combinar los resultados.

Otro ejemplo de cómo la escala de análisis condiciona los resultados obtenidos lo encontramos en el caso de efectuar mediciones. Como puede verse en la figura 9.4, la unidad de medida empleada provoca que se obtengan resultados distintos.

La unión del valor resultante con la escala a la que se ha obtenido tiene en conjunto pleno significado, pero ese valor por sí mismo carece de dicho significado.

El concepto de fractal tiene una implicación directa en este hecho.

El propio formato de almacenamiento condiciona el efecto de la escala, ya que puede imponer límites. Tal es el caso cuando se trabaja con capas raster, en las que el tamaño de celda delimita la precisión que puede obtenerse en el análisis.

El Problema de la Unidad de Área Modificable

Muchas de las variables con las que trabajamos dentro de un SIG no pueden medirse de forma puntual, y por ello han de estudiarse para un área dada. Ejemplos de este tipo de variables son el porcentaje de población en un rango de edad determinado o la densidad media de población.

Las áreas que se definen para poder trabajar con las variables de esta índole son esencialmente arbitrarias, tales como países, regiones o distritos, que se establece sin ningún criterio propio del análisis espacial. La utilización de una u otra unidad altera los resultados extraídos de las variables estudiadas.

Este problema, por tener relación con la elección de la unidad de agregación de la información, se conoce como Problema de la Unidad de Área Modificable (PUAM).

Un problema particular relacionado con el PUAM es la denominada falacia ecológica, que consiste en asumir que los valores calculados para una unidad de área pueden aplicarse a los individuos de la población existente en dicha área. Sólo en el caso de que exista una completa homogeneidad para la variable analizada, lo cual raramente sucede, la anterior suposición sería cierta.

Autocorrelación espacial

Se denomina autocorrelación espacial a la existencia de una correlación de la variable consigo misma, de tal modo que los valores de esta variable en un punto guardan relación directa con los de esa misma variable en otros puntos cercanos. Por ejemplo, en el caso de medirse la temperatura, los puntos cerca de un foco de calor tendrán una temperatura mayor que aquellos cerca de focos fríos. Si estudiamos la distribución de una enfermedad infecciosa, es más probable que los casos se encuentren agrupados, de forma que la presencia de un alto número de casos implique también una alta incidencia en poblaciones cercanas.

Otra forma de expresar la autocorrelación espacial es mediante la conocida como Primera Ley Geográfica de Tobler, que establece que «todo está relacionado con todo, pero las cosas próximas entre sí están más relacionadas que las distantes».

La autocorrelación espacial, tal y como se ha descrito antes, es positiva. Puede, no obstante, existir una autocorrelación espacial negativa, si los valores altos se rodean de valores bajos y viceversa.

En caso de no existir ningún tipo de autocorrelación espacial, se tiene que los datos recogidos en una serie de puntos son independientes entre sí y no se afectan mutuamente, sin que tenga influencia de la distancia.

La figura 9.5 muestra unas sencillas capas ráster en las que se presentan los tres tipos de autocorrelación espacial anteriores.

Las consecuencias de la existencia de autocorrelación espacial son numerosas y de gran importancia.

Por una parte, muchos de los análisis estadísticos suponen la independencia de la variable. Puesto que existe una dependencia de la componente espacial, será necesario para obtener resultados correctos introducir dicha componente espacial como una variable más.

Algo similar sucede cuando los datos presentan alguna tendencia espacial (los valores de una variable están relacionados con sus propias coordenadas geográficas), ya que esto tambien invalida el supuesto de la independencia de los datos.

Existiendo autocorrelación espacial, y siendo esta positiva, la inferencia estadística es menos eficaz que si se cuenta con un número igual de observaciones de una variable independiente.

La autocorrelación espacial no es, no obstante, un elemento que siempre tenga consecuencias negativas. Puesto que los puntos cercanos a uno dado guardan relación con este, la autocorrelación puede aprovecharse para estimar valores en un punto cualquiera si conocemos los valores en puntos cercanos. Este es el fundamento de los métodos de interpolación

Existencia de estructura

Tanto la disposición de los datos como las propiedades de la variable estudiada (por ejemplo, la propia autocorrelación espacial como propiedad intrínseca) exhiben una estructura determinada. Esta estructura puede condicionar los resultados del análisis y tener influencia sobre estos.

Los dos principales conceptos estadísticos que definen la estructura espacial de los datos son la estacionaridad y la isotropía. La estacionaridad indica que el proceso es invariante a la traslación. Es decir, que las propiedades son constantes en el espacio y no existe tendencia alguna. La isotropía indica que el proceso es invariante a la rotación y tiene lugar del mismo modo en todas direcciones.

Efectos de borde

Las zonas que estudiamos dentro de todo análisis espacial tienen unos límites establecidos. Estos límites vienen definidos de forma artificial —el límite de la fotografía aérea de la que disponemos, por ejemplo— o bien de forma natural —si estudiamos un bosque junto a un pantano, el bosque encuentra su límite al borde de este último—. La presencia de estos bordes distorsiona el resultado de los análisis, en especial para aquellos parámetros no puntuales que requieren la definición de un area de estudio (densidades, etc., como ya vimos para el caso del PUAM)

En algunos casos, el efecto de borde no se manifiesta únicamente para puntos cercanos a dicho borde, sino para todos aquellos relacionados o conectados con él según un determinado criterio, con independencia de su distancia a este.